

 Vol. 41 (Nº 02) Ano 2020. Pág. 8
Vol. 41 (Nº 02) Ano 2020. Pág. 8
ROLOFF, Micheli C.S. 1 & ROLOFF, Mário L. 2
Recebido: 08/08/2019 • Aprovado: 20/01/2020 • Publicado 31/01/2020
RESUMO: Apresentam-se aqui estratégias desenvolvidas nas aulas de Introdução ao Cálculo de um curso de Engenharia com objetivo de melhorar os indicadores de eficiência/eficácia. Em especial, trata-se do estudo das funções, a partir de deslocamentos verticais e horizontais, reflexões e expansões, visando contextualizar tais conhecimentos em situações da engenharia. Constata-se que essas ações contribuíram positivamente nos indicadores de eficiência/eficácia – combatendo a evasão – do curso, principalmente nos primeiros semestres. Os resultados alcançados at são discutidos no final deste artigo. |
ABSTRACT: Here are presented strategies developed in the classes of Introduction to Calculus of an Engineering undergraduate course with the objective of improving efficiency/effectiveness indicators. In particular, it is presented the study of functions, from vertical and horizontal displacements, reflections and expansions, in order to contextualize such knowledge in engineering situations. These actions have contributed positively to the efficiency/effectiveness indicators - combating evasion, especially in the first semesters. The results achieved so far are discussed at the end of this article. |
Quando da criação de um curso de engenharia, diversos aspectos são levados em conta, como legislação a ser atendida, aspectos do contexto educacional, como público alvo e perfil do egresso, e ainda o contexto mercadológico, entre tantos outros aspectos. Na grande maioria dos cursos do Brasil, um grupo de docentes, denominados “Colegiado de Curso” constrói o Projeto Pedagógico do Curso (PPC), que “promete” entregar à sociedade um profissional que passou por um processo de formação em um determinado período.
Certamente o perfil deste profissional está baseado nos processos formativos daqueles professores que construíram o PPC, onde cada um pôde “defender” os seus interesses, prioridades e formações.
Então, no primeiro semestre do curso de engenharia, os alunos são recebidos pelos professores de matemática, física, química, metodologia científica, introdução à engenharia, e outros. Neste momento nós professores acabamos percebendo que a clientela que se apresenta e o público alvo descrito no PPC não são exatamente o perfil esperado.
Percebemos fortemente dois aspectos que descrevem a clientela que chega aos cursos de engenharia, em especial a Engenharia Mecatrônica do Instituto Federal Catarinense (IFC) – Campus Rio do Sul. O primeiro deles diz respeito ao processo de seleção para o ingresso ao curso: ENEM, cotas (escola pública, negro, pardo, indígena) e histórico escolar. Com isto, a instituição recebe acadêmicos com amparo financeiro e familiar e também acadêmicos que necessitam de auxílios financeiros e até mesmo ingressar no mercado de trabalho para garantir o seu sustento. Percebemos então que a garantia de acesso e a permanência no curso não são igualitários.
O segundo deles, é a enorme deficiência de aprendizagem acumulada pelos jovens. De acordo com a reportagem do G1 Educação (FAJARDO & FOREQUE, 2018) com os resultados do Sistema de Avaliação da Educação Básica (SAEB), realizada pelo INEP/MEC, quase 71% dos estudantes não sabem o esperado em Língua Portuguesa ao final do Ensino Médio e cerca de 72% possuem nível insuficiente em Matemática, sendo que 24% desses estão no nível zero, o mais baixo. Ou seja, um grande número de alunos termina o Ensino Médio sem ter contato com os assuntos considerados básicos para progressão no estudo superior.
Neste contexto, acontece a primeira estratégia para tratar a evasão, o levantamento do nível de conhecimento em Matemática dos alunos. Os resultados apresentados por Fajardo e Foreque (2018) são verificados por meio da aplicação de um teste de sondagem aos ingressantes do curso de Engenharia Mecatrônica no IFC – Campus Rio do Sul. Neste teste, foi sondado o conhecimento dos alunos sobre as operações com frações, expressões numéricas, potenciação, radiciação, equações do 1º grau e do 2º grau, equações logarítmicas, identidades trigonométricas e trigonometria. Os resultados do teste comprovam os dados apresentados.
Não raro os acadêmicos buscam justificar seu baixo rendimento ou a falta de conhecimentos básicos com a seguinte frase: “professor(a), eu fiz escola pública!”, como se escola pública fosse sinônimo de ensino de má qualidade.
Também é sabido que há uma carência de professores nas áreas de Matemática, Física, Química e Ciências e aqueles professores que lecionam nestas áreas empregam metodologias tradicionais de ensino, salários defasados, com pouca ou nenhuma infraestrutura para implementar quaisquer mudanças em suas aulas.
Inevitavelmente todo este cenário impacta na trajetória acadêmica dos estudantes de qualquer curso superior que exijam tais conhecimentos prévios, assim como os acadêmicos das engenharias, fazendo com que parte do tempo universitário seja empregado para adaptação do estudante às necessidades das carreiras de Engenharia.
Segundo as Diretrizes Curriculares para Cursos de Engenharia aprovada pelo Ministério da Educação/Conselho Nacional de Educação do Brasil, o acadêmico ao longo do Curso de Engenharia deve desenvolver competências gerais, entre as quais:
II - analisar e compreender os fenômenos físicos e químicos por meio de modelos simbólicos, físicos e outros, verificados e validados por experimentação:
a) ser capaz de modelar os fenômenos, os sistemas físicos e químicos, utilizando as ferramentas matemáticas, estatísticas, computacionais e de simulação, entre outras.
b) prever os resultados dos sistemas por meio dos modelos;
c) conceber experimentos que gerem resultados reais para o comportamento dos fenômenos e sistemas em estudo.
d) verificar e validar os modelos por meio de técnicas adequadas;
O cenário atual é este, discentes deficitários e novas propostas para ensino de engenharia que necessitam ser implantadas. Neste contexto, e pensando nas aplicações ao longo do curso bem como em suas futuras atuações profissionais, propomos que o estudo das funções possua outro enfoque na disciplina de Introdução ao Cálculo do curso de Engenharia Mecatrônica do IFC – Campus Rio do Sul.
Temos percebido em nossas jornadas acadêmicas e docentes que o estudo de funções, no contexto brasileiro, foi resumido a identificar as raízes, determinar os conjuntos domínio e imagem, estudo do sinal, análise de paridade e intervalos de crescimento e decrescimento. Por exemplo, o estudo da parábola, como função quadrática
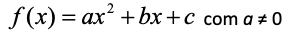 (1)
(1)
tem se resumido a identificar os valores de a, b e c, determinar as raízes, caso existam, esboçar o gráfico da parábola, observando a concavidade do gráfico, os pontos que interceptam os eixos e e por fim, os pontos de máximo ou de mínimo da função (vértice).
Para comprovar nossa afirmação, analisamos alguns livros didáticos, disponibilizados pelo Plano Nacional do Livro Didático – PNLD 2018, para compreendermos como os alunos estudam funções no Ensino Médio, bagagem esta que deveriam trazer consigo. Analisamos o estudo da parábola, como função quadrática, observa-se que alguns autores vão além dos tópicos citados anteriormente e apresentam a forma canônica explorando outros detalhes, que talvez não são desenvolvidos em sala de aula. A Tabela 1, resume a análise de livros didáticos do 1º ano do ensino médio, onde o conteúdo de Função Quadrática é abordado.
Tabela 1
Análise de livros didáticos
do 1º ano do Ensino Médio
Obra |
a) |
b) |
c) |
d) |
e) |
f) |
g) |
h) |
CHAVANTE e PRESTES, 2016 |
x |
x |
|
|
|
x |
x |
x |
DANTE, 2016 |
x |
x |
|
|
x |
x |
x |
x |
IEZZI, et. al., 2016 |
x |
x |
x |
x |
x |
x |
|
x |
SMOLE e DINIZ, 2016 |
x |
|
x |
x |
|
x |
|
|
SOUZA e GARCIA, 2016. |
x |
|
|
|
|
|
|
x |
Fonte: Os autores
Legenda dos itens analisados:
No entanto, há outras maneiras de estudar as funções, como propõe STEWART (2015), a partir de deslocamentos horizontais e verticais, expansões, compressões e reflexões.
Ao ser apresentado o conteúdo de Função Quadrática aos 46 acadêmicos ingressantes do curso de Engenharia Mecatrônica em 2018, percebemos que todos haviam estudado o conteúdo no ensino médio, porém limitado a determinação das raízes, utilizando a fórmula de Bhaskara ou por soma e produto das raízes, deste total, um grupo de 8 alunos relatou que desconheciam a regra para determinar a solução por soma e produto das raízes.
Fora gratificante explorar a parábola na forma canônica
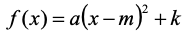 (2)
(2)
que permite analisar os deslocamentos horizontais e verticais, e a determinação do vértice da parábola (mínimo ou máximo), cujas coordenadas são . Diferentemente dos problemas explorados no Ensino Médio (determinação das raízes), os problemas físicos, químicos, programação e outras áreas da engenharia (como controle de procesos), frequentemente requerem conhecer as coordenadas do vértice, desta forma é mais conveniente o estudo da parábola na forma canônica.
Neste momento vale ressaltar que acreditamos na matemática como uma ferramenta nos cursos de engenharia, que ajuda no desenvolvimento do raciocínio, na estratégia de solução de problemas e como parte criativa de algumas situações da engenharia. Assim, não estamos preocupados em demostrar teoremas, ou que nossos alunos saibam provar que é um número irracional, defendemos que isso cabe aos alunos dos cursos de licenciatura e bacharelado em Matemática.
Neste contexto, é necessário um esforço docente que vai além das aulas presenciais de Introdução ao Cálculo. O docente necesita buscar estratégias para combater a evasão, cuja a causa maior é a deficiencia na formação de Ensino Médio dos alunos. Nestes últimos anos foram selecionadas e aprimoradas algumas ferramentas para combater o déficit de aprendizagem nos alunos ingressantes do curso de Engenharia Mecatrônica que serão descritas a seguir.
O primeiro ponto, buscar minimamente que nossas aulas sejam diferentes daquelas que nossos alunos tiveram ao longo do Ensino Médio. Assim, busca-se por métodos, técnicas ou tecnologias que propiciem uma experiência diferente para os alunos. Por exemplo, para apresentar ou relembrar as funções, os alunos receberam inicialmente uma folha, com várias imagens que simbolizam algumas funções, conforme a Figura 1.
Figura 1
Gráfico de algumas funções
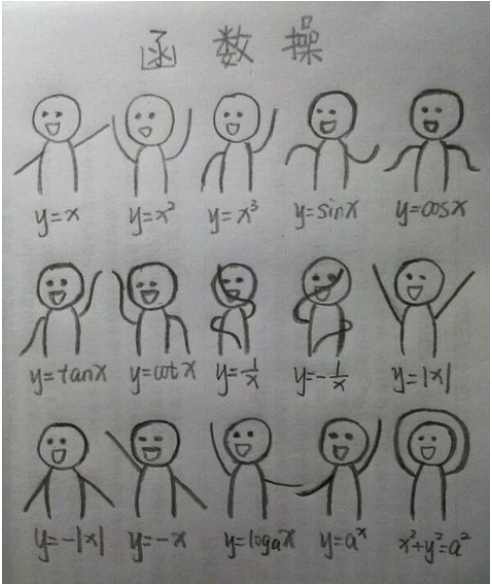
Fonte: Blog Ciência Online (2018)
-----
Quando alguma função específica é estudada, por exemplo a Função Quadrática, a mesma é retomada a partida da Figura 1, definida matematicamente e em seguida as transformações são exploradas, com a ajuda de uma síntese, intitulada Transformações de Funções, conforme as Figuras 2 e 3.
Figura 2
Deslocamentos verticais e horizontais

Fonte: Adaptado de Stewart, 2015
-----
Figura 3
Reflexões e expansões verticais e horizontais

Fonte: Adaptado de Stewart, 2015
Uma vez compreendidos a definição e as transformações, os alunos são desafiados a construir o gráfico de algumas funções aplicando as transformações estudas (Figura 2 e 3), a partir de um gráfico conhecido, conforme a Figura 4.
Figura 4
Construção de gráficos
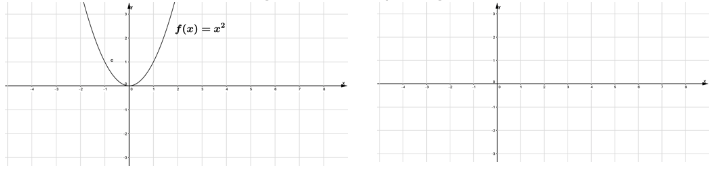
Fonte: Os autores
Contudo, apenas as aulas, mesmo com abordagens criativas, definidas no horário do aluno não são suficientes para recuperar a defasagem de muitos ingressantes no curso de Engenharia. Diante deste cenário, são adotadas algumas outras ações:
Este assunto será retomado no final do artigo onde os resultados alcançados serão apresentados. Na seção seguinte se apresenta outra estratégia que consideramos relevante para combater a evasão e associada com as estratégias anteriores produziu bons resultados no curso de Engenharia Mecatrônica.
Esta seção possui o objetivo de contextualizar as funções na engenharia afim de comprovar a necessidade de se abordar o estudo de funções diferentemente do que vem sendo feito nas escolas de engenharia brasileiras.
Em muitas situações da engenharia conhecimentos matemáticos são requisitados como ferramentas necessárias ao desenvolvimento de produtos, softwares e melhoria de processos. No entanto, estes conhecimentos matemáticos precisam estar organizados de maneira a facilitar sua aplicação no projeto de uma máquina, no controle de um determinado processo e em muitos casos, para a comunicação eficaz em um equipe.
Por exemplo, ao programar o termostato de um forno ou estufa, devemos limitar a temperatura máxima, após o start. Do início do processo até a temperatura máxima, a curva que descreve a temperatura em função do tempo pode ser analisada como uma função quadrática e a temperatura máxima, requerida em nossa situação problema é justamente o vértice da parábola, cujas coordenadas são se escrita na forma canônica conforme a Equação (2).
Outros tantos exemplos da engenharia são baseados na Função Quadrática, problemas de objetos lançados, crescimento de população, diversas abordagens para o controle de processos, estratégias de acionamentos de motores, inúmeros algoritmos computacionais (como na área de processamento digital de imagens ), trajetórias de robôs ou veículos autónomos, etc.
Outro exemplo aparece na análise de circuitos elétricos, as correntes alternadas são descritas pela função seno. E quando escrevemos a função como
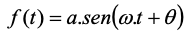 (3)
(3)
onde a constante indica a amplitude da corrente elétrica (em Amperes) ou tensão elétrica (em Volts), a constante indica a velocidade angular da onda (em rad/segundo) e a constante é a defasagem da onda (em rad ou graus). Se analisarmos a ação destas constantes como transformações no gráfico da função seno, temos que gera uma expansão vertical por um fator alterando o conjunto imagem da função, comprime o gráfico horizontalmente por um fator alterando o período da função seno para e por fim desloca o gráfico para a direita ou esquerda unidades.
Enfim, estes e muitos outros envolvem o estudo do ponto máximo de uma função e um dos nossos objetivos com este artigo é chamar a atenção para os benefícios que uma abordagem de ensino-aprendizagem que se preocupa em entender qual é o seu público em sala de aula, como cada conteúdo pode/deve ser apresentado de forma a justificá-lo e contextualizá-lo durante o processo de formação do perfil profissional, perfil profissional este sintonizado com as expectativas do mercado.
Dos 46 alunos ingressantes no ano de 2018, 34 seguiram a disciplina até o fim e 29 foram aprovados em Introdução ao Cálculo. Em Cálculo 1, dos 29 alunos, 24 seguiram até o fim da disciplina, e 23 foram aprovados. Para o Cálculo 2, o 3º semestre para a turma de 2018, apenas 20 retornaram e realizaram matrícula. Ou seja, um ano após o ingresso, temos pouco menos de 50% dos alunos ingressantes cursando a disciplina de Cálculo 2.
Destes 20 alunos, 17 foram entrevistados para este estudo. Esses alunos foram questionados sobre suas práticas quanto ao Horário de Atendimento, a Síntese Escrita, e a Lista de Exercícios. Também perguntamos se o Gráfico das Funções (Figura 1) foi útil, e/ou se tem ajudado em outras disciplinas. Fizemos a mesma pergunta sobre a utilização dos deslocamentos horizontais e verticais, reflexões e expansões (Figuras 2 e 3). E ainda, neste mesmo sentido, sobre o estudo da parábola na forma canônica (Equação 2). Passaremos então a relatar as percepções dos alunos:
Com o término da disciplina de Cálculo 2, dos 20 alunos matriculados, 19 seguiram até o fim, e destes, 17 foram aprovados. Agora seguem para o 4º semestre do curso, pouco menos de 37% dos ingresantes em 2018. Contudo, esses alunos demonstram maturidade em seus conhecimentos matemáticos que propiciam a continuidade, sem percausos, na sua formação em engenharia.
É sabido que o modelo tradicional mostra esgotamento na relação professor-aluno, contudo, constatamos que essa crise paradigmática que vivemos é a oportunidade para implantar, experimentar e aprimorar novas estratégias de ensino-aprendizagem.
A primeira constatação é que é preciso não ter medo de fazer diferente, de inovar, e principalmente do professor de abrir mão do seu papel de ator principal e se colocar em outra posição – talvez assumir o papel de mentor atuando na organização, no direcionamento do aprendizado e tutoria dos alunos. Acreditamos que nas abordagens ativas, o professor assume o papel de mentoria, que vai além da função de transmissor de informação. Ser uma fonte de conhecimento teórico/prático e o transferir esse conhecimento (competências e habilidades) para o aluno continuam. Contudo, o professor na engenharia ativa atua também na formação comportamental (atitudes) dos alunos pois essa abordagem privilegia uma atuação mais próxima professor-aluno. O professor passa a estar ´mais disponível´ para o aluno e automaticamente o aluno se sente mais seguro de consultar o professor sobre assuntos de caráter técnico e também ético (atitudes).
Cabe aquí ressaltar que os autores tiveram suas graduações concluídas em uma das melhores universidades brasileiras sendo destaque latino americana nos cursos de engenharia, principalmente no seu relacionamento com as indústrias. Contudo, isso não reduziu o impacto do final da graduação com o início da atividade profissional, na atuação como professor ou na atuação como profissional de engenharia. Essa sensação de um grande abismo entre o conteúdo recebido e a realidade contribuiu para dedicarmos nossa atuação profissional na redução desse gap semântico entre o ambiente acadêmico e o ambiente profissional. Outro fator motivador é o feedback constante dos empresários afirmando que o recém formado, para estar apto a atuar profissionalmente na sua empresa, necessita participar de um programa trainee. Somente após esse treinamento de 6 até 12 meses o profissional estará minimamente preparado ao exercício profissional na empresa. Enfim, a grande maioria dos empresários argumentam que a graduação não traz formação suficiente para o profissional que a empresa necessita. Estamos atuando para mudar esse cenário.
Acreditamos pelas nossas experiências acadêmicas e docentes na memorização de algumas fórmulas e estratégias como ferramenta que agilizam alguns cálculos. Acreditamos também que não faz sentido memorizá-las caso não sejam compreendidas dentro do contexto de formação do engenheiro. Especialmente no início do curso é fundamental que os professores atuem em suas disciplinas isoladas ou em conjunto de forma a responder a pergunta que ouvimos todo semestre: Para que eu preciso aprender isso? Por que tem que ser desta forma? Por isso, buscamos contextualizar nossas aulas com situações próximas do cotidiano do futuro engenheiro e entregando ferramentas que efetivamente farão parte do seu dia-a-dia profissional.
Lima (2017) argumenta: “[...] quanto mais ativo, crítico e reflexivo for esse processo, maiores serão as chances para produzirmos mudanças na educação e na sociedade”. É neste contexto que gostaríamos de encerrar este artigo, necessitamos realizar mudanças profundas em muitos cursos de Engenharia do Brasil, contudo, as mudanças não são necessariamente drásticas, muitas delas são ações que impactam na forma de apresentar o conteúdo, de compreender seu público alvo e de qual é a meta a ser alcançada ao final do semestre, ou melhor, quais são as competências, habilidades e atitudes mínimas esperadas dos discentes que os tornem APTOS a seguir em frente.
Por fim, desejamos explicitar apoio às Diretrizes Nacionais para Cursos de Graduação de Engenharia homologada pelo MEC/CNE neste ano que defende um processo de ensino-aprendizagem contextualizado com desenvolvimento de competências, habilidades e atitudes orientadas ao mercado como a estratégia para a formação do engenheiro do futuro.
Blog Ciência Online. Disponível em: http://www.ciencia-online.net/2014/03/as-funcoes-matematicas-graficas-como.html?m=1. Acesso em: 14 jan 2018
CHAVANTE, Eduardo; PRESTES, Diogo. Quadrante matemática: 1º ano. 1.ed. São Paulo: Edições SM, 2016.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Volume 1. 3.ed. São Paulo: Ática, 2016.
FAJARDO, Vanessa; FOREQUE, Flavia. G1 Educação. 7 de cada 10 alunos do ensino médio têm nível insuficiente em português e matemática, diz MEC. Disponível em: https://g1.globo.com/educacao/noticia/2018/08/30/7-de-cada-10-alunos-do-ensino-medio-tem-nivel-insuficiente-em-portugues-e-matematica-diz-mec.ghtml. Publicado em: 30/08/2018. Acesso em: 09 maio 2019.
IEZZI, Gelson. Fundamentos de matemática elementar 7: geometria analítica. 8.ed. São Paulo: Atual, 2010.
IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto; ALMEIDA, Nilze de. Matemática: ciência e aplicações. Volume 1. 9.ed. São Paulo: Saraiva, 2016.
IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de matemática elementar 1: conjuntos e funções. 8.ed. São Paulo: Atual, 2010.
LIMA, Elon Lages. Curso do Programa de Aperfeiçoamento de Professores de Matemática do Ensino Médio - Professor Elon Lages Lima - IMPA – 2001. Disponível em: https://www.youtube.com/watch?v=rm8L-C7024M. Acesso em: 06 abril 2018.
LIMA, Valéria Vernaschi. Espiral construtivista: uma metodologia ativa de ensino aprendizagem. Constructivist spiral: an active learning methodology. Interface - Comunicação, Saúde, Educação. 21, 61, 421-434, Apr. 2017.
MEC/CNE. Ministério da Educação/Conselho Nacional de Educação. Diretrizes Curriculares Nacionais do Curso de Graduação em Engenharia. PARECER CNE/CES Nº: 1/2019. APROVADO EM: 23/1/2019. Disponível em: http://portal.mec.gov.br/index.php?option=com_docman&view=download&alias=109871-pces001-19-1&category_slug=marco-2019-pdf&Itemid=30192. Acesso em: 09 maio 2019.
SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Matemática para compreender o mundo 1. 1.ed. São Paulo: Saraiva, 2016.
SOUZA, Joamir Roberto de; GARCIA, Jacqueline da Silva Ribeiro. #Contato matemática, 1º ano. São Paulo: FTD, 2016.
STEWART, JAMES. Cálculo: Volume 1. São Paulo: Cengage Learning, 2015.
1. Mestre em Educação (UNIVALI, Brasil). Licenciada em Matemática (UFSC, Brasil). Docente do Instituto Federal Catarinense – Campus Rio do Sul. micheli.roloff@ifc.edu.br
2. Doutor em Engenharia de Automação e Sistemas (UFSC, Brasil). Bacharel em Controle e Automação Industrial (UFSC, Brasil). Docente do Instituto Federal Catarinense – Campus Rio do Sul. mario.roloff@ifc.edu.br
[Índice]
revistaespacios.com

Este trabalho está sob uma Licença Creative Commons
Atribuição-Uso Não-Comercial 4.0 Internacional