

 Vol. 40 (Nº 33) Año 2019. Pág. 28
Vol. 40 (Nº 33) Año 2019. Pág. 28
BRAVO-SANZANA, Mónica V. 1; PAVEZ, Matías, I. 2; SALVO-GARRIDO, Sonia I. 3 y MIERES-CHACALTANA, Manuel, S. 4
Recibido: 23/06/2019 • Aprobado: 26/09/2019 • Publicado 30/09/2019
RESUMEN: El objetivo de este estudio fue obtener perfiles de desempeño a través de los factores que inciden en el rendimiento académico de Matemática, en una muestra representativa regional de estudiantes de secundaria en La Araucanía, Chile. Metodológicamente, se utilizaron técnicas estadísticas conocidas como bosque aleatorio (RF) y árbol de clasificación y regresión (CART). Los principales factores evidenciados fueron: autoeficacia en Matemática, expectativas educacionales de padres y estudiantes y, como factor de clima social escolar, la violencia percibida por los padres. |
ABSTRACT: This study aim was to obtain performance profiles by means of the factors which affect the academic performance in mathematics, in a regionally representative sample of high school students in La Araucanía, Chile. In regards to methodology, statistical techniques known as random forest (RF) and classification and regression tree (CART) were used. The main factors evidenced were: self-efficacy in mathematics, parents and students’ educational expectations and, as a factor of school social climate, parents’ perceived violence. |
La investigación en educación ha señalado que existen diferentes factores que intervienen dentro y fuera del aula y que tienden a condicionar el aprendizaje y enseñanza de las distintas asignaturas escolares en América Latina (Murillo y Garrido, 2017). Los estudios que se dedican a la exploración de factores asociados a los logros de aprendizaje escolar, tienen por finalidad relevar factores individuales o personales y factores de contexto que influencian los logros de aprendizaje para disponer de insumos que colaboren en la toma de decisiones en los procesos de intervención educativa (Gamazo et al., 2018; Martínez-Abad et al., 2017; Murillo y Garrido, 2017).
Actualmente, uno de los indicadores de calidad de la educación es el rendimiento académico (MINEDUC, 2016a), medida de aprendizaje expresada a través del esfuerzo y capacidad de trabajo desde lo cognitivo y desde las competencias adquiridas a lo largo de su proceso de aprendizaje. La literatura en educación sostiene que un bajo rendimiento escolar puede generar factores psicológicos negativos como altos niveles de depresión, baja autoestima que afectan el bienestar de los estudiantes (Robert et al., 2014) y deserción escolar por agresiones como burlas por bajo rendimiento (Ruíz-Ramírez, et al., 2018). En este sentido, el rendimiento académico no es influenciado solo por lo cognitivo, sino que también intervienen factores relacionados al contexto cultural, familiar, escolar, e individual como la emocionalidad del sujeto que aprende (Yu & Singh, 2018; Ng, 2018).
Entre los factores de contexto familiar que se asocian con el logro académico en Matemática, Bravo-Sanzana, Salvo & Muñoz (2015), evidenciaron que las expectativas educacionales de los padres son predictores significativos en el rendimiento académico. Incluso las expectativas de los mismos estudiantes, como factor individual, actúan como mediador entre las habilidades en Matemática y el logro en este dominio, coincidiendo con el estudio de Doménech-Betoret, Abellán-Roselló & Gómez-Artiga (2017). Así también Din, Ayub & Tarmizi (2016), revelaron que la participación de los padres presenta una relación positiva con el compromiso que asume el estudiante con la Matemática en el aula.
Otro de los factores de contexto familiar, es el número de libros en el hogar. La literatura ha sostenido que existe una asociación positiva y predictiva entre una mayor cantidad de libros en el hogar-como una forma de capital cultural de la familia (Bourdieu, 1979)- y un mejor desempeño académico (Chaparro, González, y Caso, 2016), especialmente cuando el proceso de estimulación cognitivo y del lenguaje de los niños y niñas se realiza tempranamente con el uso de los libros (Tomopoulos et al., 2006).
Entre los factores individuales, la literatura especializada ha mostrado el importante rol que tiene la autoeficacia (o teoría de la autoeficacia); desarrollada por Albert Bandura en 1977, corresponde a las creencias que tiene un sujeto sobre sus propias capacidades y, por tanto, está relacionado con procesos cognitivos, motivacionales, afectivos y conductuales (Bandura, 1977, 1994). Aplicado al contexto educativo, el apoyo de los profesores como un factor de contexto escolar, representa una influencia indirecta sobre el desempeño en Matemática por medio de la autoeficacia, influyendo, finalmente, sobre el interés de la asignatura (Yu & Singh, 2018). Según Usta (2016), con base a las respuestas obtenidas en los cuestionarios de estudiantes de PISA 2012 de China-Shangai, Turquía y Grecia, la autoeficacia de los estudiantes en Matemática aumentaba conforme existía mayor apoyo y comunicación del docente. En el caso de Turquía, mostró que existen antecedentes de que la autoeficacia en Matemática es la variable que presenta mayor contribución en el logro académico de Matemática y actúa como el mayor predictor de la alfabetización en este dominio, coincidiendo con otros estudios (Kogar, 2015; Şahin & Yıldırım 2016; Recber, Isiksal & Koc, 2017; Cetin & Gok, 2017).
Así también, Akgul, Cokamay & Demir (2016), considerando los resultados de PISA 2012 de estudiantes de secundaria provenientes de Turquía y Shangai, encontraron que tanto la autoeficacia en Matemática como la actitud hacia la escuela fueron predictores del apoyo docente en ambos países. Otros estudios dan cuenta que, a partir de los factores intrapersonales del estudiante, la autoeficacia en Matemática corresponde a la variable que mayoritariamente explica el logro académico en este dominio (Tosto et al., 2016; Kamalimoghaddam et al., 2016; Ahn et al., 2016). Lo anterior, confirma lo mencionado por Bandura (2002), al señalar que la autoeficacia corresponde a un predictor del desempeño académico transversal a toda cultura.
Otros factores relevantes informados por la investigación en educación, son aquellos relacionados con el ambiente escolar (Benbenishty et al., 2016), lo que la literatura reporta como Clima Social Escolar (CSE, en adelante), comprendido como las percepciones afectivas y cognitivas con respecto a las interacciones sociales, las relaciones, los valores y las creencias de los estudiantes, maestros, administradores y personal dentro de una escuela (Rudasill et al., 2018). Desde la psicología, el modelo ecológico de Bronfenbrenner (1987) nos aporta una mirada amplia e integral focalizada en el ambiente y su influencia en el desarrollo cognitivo, relacional y moral de la persona. Este enfoque multidimensional nos permite acercarnos al ambiente escolar especialmente respecto de la interacción social que se genera en la escuela (Claro, 2013), sobre la calidad de vida en dicho entorno, con relación a las normas, valores, procesos y estructuras organizacionales (Kumari & Dhull, 2017; Vargas et al., 2018). Involucra las interacciones tanto a nivel del aula, como de la institución, involucrando a toda la comunidad educativa. De acuerdo a esta comprensión y a la mirada ecológica del constructo, el CSE es un constructo dinámico, en desarrollo y que, por tanto, puede ser objeto de estudio para su comprensión, mejora e influencia positiva en el proceso integral de formación de los estudiantes y su bienestar (Bravo-Sanzana, Salvo y Mieres-Chacaltana, 2015, 2016), y la motivación de los profesores se refuerza al tener un buen clima social escolar en su escuela, relevándose las relaciones interpersonales, la satisfacción con el trabajo realizado y el ambiente laboral para su buen desempeño (López, Efstathios, y Herrera,2018).
En Europa, en los últimos años, ha emergido un creciente interés en estudiar el CSE y su efecto en el rendimiento académico de los estudiantes, de manera que se establezcan políticas educativas que promuevan un ambiente de aprendizaje óptimo. En el caso de Chile, y América Latina en general, las investigaciones en clima escolar son escasas (Berger et al., 2014), y sumado a lo anterior, la Región evidencia bajos indicadores de desempeño académico en Matemática (MINEDUC, 2015; OCDE, 2016b). En este sentido, se establece la necesidad de estudiar el ambiente escolar y los factores asociados a la Educación Matemática que influencian el desempeño académico en este dominio.
Específicamente en Matemática, el desempeño de los estudiantes chilenos se ha visto estancado sin tener avances significativos tanto en pruebas internacionales como nacionales (OCDE, 2016; MINEDUC, 2015, 2016b, 2017). Elementos claves para analizar variables de contexto, son el CSE y la familia, debido a que actúan como predictores de la competencia emocional respecto del rendimiento académico y como predictores de la violencia entre pares (Ruvalcaba-Romero, Gallegos-Guajardo y Fuerte Nava, 2017).
Respecto a CSE y desempeño académico, las investigaciones han señalado su directa relación pues un buen ambiente escolar promueve el logro de buenos aprendizajes (Çengel & Türkoğlu, 2016), además, es clave el estudio del CSE y la participación de la familia con las instituciones educativas (Garbacz et al., 2017). En este sentido, un CSE positivo está asociado a la alta participación de la comunidad estudiantil y a bajos niveles de agresión y de violencia escolar (Konold et al., 2017) pudiendo actuar como agente protector para aquellos estudiantes que presentan estructuras familiares monoparentales o sin hogar (O’malley et al., 2015). Por el contrario, los colegios que presentan climas escolares negativos tienden a desarrollar mayor cantidad de conductas agresivas como la violencia escolar, definida como cualquier amenaza o asalto físico o psicológico entre pares o maestros en la escuela, implicando abuso verbal e intimidación para conductas de robo, violación y homicidio (Akiba, Shimizu, & Zhuang, 2010). Además, las escuelas con ambientes escolares negativos se caracterizan por presentar una mayor limitación en la relación entre compañeros y una alta probabilidad de sufrir intimidación escolar, la cual llega a ser hasta cuatro veces mayor que la de colegios en donde el CSE es adecuado (Çengel & Türkoğlu, 2016; Moratto, Cárdenas y Berbesi, 2017). Un estudio reciente mostró que en Colombia y Perú la violencia verbal entre estudiantes y la disrupción en el aula de clase eran los factores de violencia escolar predominantes (Henning et al., 2018). En el caso de Chile, un estudio señaló que el factor más presente asociado al CSE negativo es la violencia escolar (Trucco y Inostroza, 2017).
Además, un estudio reciente para América Latina evidenció la influencia negativa de la violencia presente en el entorno de la escuela sobre los aprendizajes, indicando que por cada punto en que aumenta el índice de violencia percibido por los padres, los rendimientos se reducen entre ocho y 27 puntos en tercer grado y, entre ocho y 38 puntos en sexto (OREALC/UNESCO, 2015).
Los factores evidenciados por los diferentes estudios y realizados con diferentes metodologías no se presentan aislados, sino que forman parte de diferentes dimensiones contextuales por lo que interactúan. A nivel metodológico existe una técnica de clasificación y regresión, Classification and Regression Tree, CART (Breiman et al., 1984), muy utilizada en investigación de salud y recientemente en investigación educativa (Ma, 2005; Bravo et al., 2015, 2017) que agrupa a sujetos con características comunes, formando perfiles de estudiantes lo que permitirá observar cómo interactúan los factores en estos grupos para visualizar las implicancias en los procesos de mejora educativa.
Desde esta perspectiva, este estudio tiene por objetivo obtener perfiles de desempeño a través de los factores que inciden en el rendimiento académico de Matemática, en una muestra representativa regional de estudiantes de secundaria en La Araucanía, Chile.
El presente estudio tiene un enfoque metodológico cuantitativo, con un diseño de tipo no experimental, predictivo, de corte transversal (Toro y Parra, 2010).
Corresponden a una muestra representativa regional de región de La Araucanía, Chile. La selección de los participantes se realizó mediante un muestreo probabilístico estratificado multi etápico, con una confiabilidad de 99%, un 2,5% de error estimación y una varianza estimada asumiendo p=q=0,5 (Scheaffer, Mendenhall & Ott, 1987). Las unidades muestrales fueron establecidas según dependencia o tipo de establecimiento educativo (municipales 46%; particulares subvencionados por el Estado, 54%) y territorialidad (86% urbano). El diseño de muestreo consideró la participación de 2.090 estudiantes (Tamaño Poblacional: 13.490), de segundo medio, de los cuales un 52, 6% son hembras y un 47,4% varones. El promedio de edad es de 15,69 años (ds=0,71). La Araucanía se caracteriza por tener una ciudadanía con diversidad cultural, económica, social y étnica (Serra-Olivares, 2016).
Se utilizó la base de datos del Sistema de Medición de la Calidad de la Educación de Chile (en adelante, SIMCE) correspondiente a segundo año de enseñanza secundaria en el dominio de Matemática. SIMCE es un sistema censal de medición de logros de aprendizaje en diversas áreas del currículo nacional, en el cual se aplican primeramente pruebas estandarizadas que evalúan diversas asignaturas. Los resultados reportados de esta prueba se expresan en puntajes por estudiante y corresponde a la variable dependiente. Para este estudio se utilizó la prueba del dominio Matemática que incorpora la evaluación de cuatro ejes temáticos: Números, Álgebra, Geometría, Datos y Azar (MINEDUC, 2016a).
La base de datos fue etiquetada y codificada para todas las variables, indicando el cuestionario, pregunta e ítem. Fueron identificadas las categorías de vacías y de doble marca. Los ítems que fueron respondidos manualmente, como fechas y edades, fueron validados. Algunas preguntas como el nivel de estudios del padre o la madre fueron agrupadas para su mejor comprensión. La base se compuso de:
Prueba SIMCE 2015 Matemática. Los resultados reportados de esta prueba se expresan en puntajes por estudiante y corresponde a la variable dependiente. Esta es una prueba estandarizada anual para este dominio. Incorpora la evaluación de cuatro ejes temáticos: Números, Álgebra, Geometría, Datos y Azar.
Cuestionarios de Calidad y Contexto de la Educación. A fin de mejorar la calidad educativa y la equidad. Son aplicados a estudiantes, profesores, padres o apoderados. En la prueba 2015 solo se aplicó cuestionarios a los docentes de Lenguaje, Ciencias e Historia. Recopilan información relacionada con aquello factores que inciden en el proceso de aprendizaje, tales como los demográficos, socioculturales y técnico-pedagógicos entre otros. El Cuestionario del Estudiante, estuvo compuesto por 42 preguntas, y el Cuestionario de Padres conformado por 29 preguntas. Ambos instrumentos miden la percepción respecto a variados temas de índole individual, familiar, relacionados con la escuela, además de recoger información sociodemográfica. Estas variables de contexto, se seleccionaron desde la revisión de la literatura realizada en el marco teórico y se utilizaron como variables predictoras del rendimiento en Matemática.
Respecto al análisis psicométrico de las pruebas SIMCE este sistema se basa en el modelo de medición de la Teoría de Respuesta al Ítem (TRI) y para la puntuación de los estudiantes se emplea la estimación Expected A Posteriori, EAP. Este modelo permite la comparabilidad de los puntajes a través del tiempo y posibilita comparar el rendimiento de diferentes cohortes, aun utilizando pruebas distintas, debido a que utiliza el procedimiento de equiparación o equating (MINEDUC, 2012, 2013).
Con relación a los procedimientos éticos del estudio, las bases de datos SIMCE son públicas para investigación previa solicitud, garantizando el buen uso de ésta y resguardando los principios éticos del estudio (confidencialidad y anonimato de la información).
Como primera fase respecto del procedimiento para el análisis de los datos, se construyeron scores referidos a información del estudiante y padres con base a cuestionarios de contexto SIMCE. Para operacionalizar el estudio, solo se describen los scores que resultaron relevantes en el análisis. Se realizó análisis factorial confirmatorio evaluando la unidimensionalidad de cada una de las escalas de los cuestionarios, para ello se utilizó la matriz de correlación policórica, adecuada para datos ordinales (Jöreskog, 1994) y el método de estimación “Weighted Least Squares Mean and Variance Adjuste” (mínimos cuadrados ponderados con media y varianza ajustada, WLSMV). Para evaluar el ajuste de los modelos a los datos se utilizó los siguientes índices de ajuste: chi-cuadrado (X2), índice de ajuste comparativo (CFI), índice de Tucker-Lewis (TLI) y error cuadrático medio de aproximación (RMSEA); para los primeros índices, CFI y TLI, se considera un ajuste adecuado del modelo los valores superiores a .90 (Schumacher & Lomax, 1996); mientras que para el RMSEA se considera un ajuste razonable los valores inferiores a .08 (Browne & Cudeck, 1993). Una vez evaluada la unidimensionalidad, se procedió a obtener los scores factoriales. Estos análisis fueron realizados con el software Mplus 7.1 (Muthén & Muthén, 1998-2012).
En la Tabla 1 se observa la dimensión, los ítems que conforman las escalas que fueron significativas en los análisis realizados, así como los índices de ajuste obtenidos y sus grados de libertad (gl) al contrastar un modelo unidimensional en cada una de ellas, los resultados muestran valores adecuados (CFI y TLI mayores o iguales a .95 y RMSEA menor a .08).
Tabla 1
Caracterización de las escalas
evaluadas unidimensionalmente
Dimensión |
Cuestionario Número e ítems |
Descripción |
gl |
CFI |
TLI |
RMSEA (90% IC) |
Rango |
Interpretación |
Autoeficacia en Matemática |
Estudiantes Pregunta 22 Ítems 01, 06, 12 y 15 |
Percepción que el estudiante tiene de su capacidad de estudio, esfuerzo, motivación hacia Matemática. |
11 |
.990 |
.969 |
.078 |
(-1,58; 1,52) |
A mayor puntaje, mayor rendimiento académico. |
Violencia Escolar percibida por los padres |
Padres Pregunta 22 Ítems 01-06 |
Percepción de los padres respecto a violencia en la escuela en diversas formas: robos, amenazas, agresiones, etc. |
9 |
.998 |
.996 |
.050 |
(-,93; 1,91) |
A mayor puntaje, menor rendimiento académico. |
Fuente: Elaboración propia con base a
Cuestionarios de Contexto SIMCE 2015.
Posteriormente, para el análisis de los datos se aplicó la técnica estadística multivariante de clasificación no paramétrica: Random Forest o “bosque aleatorio”, en adelante RF y Classification And Regression Trees, Árboles de Clasificación y Regresión, en adelante CART, perteneciente a la familia de las técnicas de árboles de decisión (Breiman et al., 1984; Ma, 2005).
Para caracterizar los grupos (perfiles) del estudiantado chileno en función de las variables relevantes se obtuvieron, entre otros indicadores, percentiles, utilizando densidades no paramétricas. Lo anterior, con la finalidad de construir una función de distribución libre basada en la información exacta de los datos y obtener resultados más estrechamente vinculados a la información real, sin imponer una distribución teórica sobre la información analizada (Silverman, 1986). Para el procesamiento de datos cuantitativos se utilizó el software estadístico JMP®10 versión de prueba .
La puntuación media en Matemáticas fue de 264.9 puntos con una desviación estándar de 62 puntos, la puntuación mínima fue de 86.9 puntos, puntaje que presenta una diferencia de 335.1 puntos respecto del máximo. Un 75% de los estudiantes de segundo medio no superó los 312.8 puntos en la prueba de Matemática, mientras que un 10% (209 estudiantes) alcanzaron puntajes superiores a 345.8 y solo 52 estudiantes (2,5%) supera los 382.5 puntos.
Con el algoritmo RF se utilizó para training un N=2.090, lo que resultó en un Ra2 =0,594 y RMSE=39.94. Para validación un N=2.090, resultando en un Ra2=0,596 y RMSE=39.83. La cercanía de ambos índices en las etapas de estimación y validación indica que el algoritmo de RF es estable en el rendimiento de los modelos.
El análisis de Random Forest (RF) incluyó 65 variables (cuestionarios de contexto) de los cuales solo 26 fueron seleccionadas. A continuación, se empleó el análisis CART para formular un único árbol de decisión con grupos. Finalmente, el árbol para Matemática, quedó conformado por cinco variables luego de haberse realizado 6 divisiones al árbol. Esta decisión está basada en que, a partir de estas divisiones, el Ra2 se estabilizó (Figura 1).
Figura 1
Aumento de R-Square en función de
las divisiones del árbol para Matemática
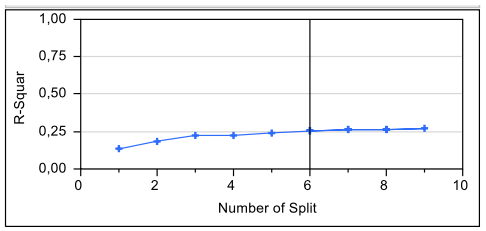
La Tabla 2 muestra las variables seleccionadas, sus porcentajes de contribución al desempeño en Matemática y los resultados del análisis CART, evidenciando la contribución de estas variables en la asignación de puntaje para la formación de grupos o perfiles.
Tabla 2
Porcentaje de contribución
de variables en modelo CART
Variables |
Descripción |
% contribución CART |
Autoeficacia en Matemática |
Variable compuesta de 4 ítems con respuestas en escala Likert (cuatro tipos de niveles de acuerdo). Hace referencia a una auto descripción del estudiante en la asignatura de Matemática a partir de su propia experiencia. Ejemplo: “Aprendo Matemática con facilidad y rapidez” |
52,81% |
Expectativas educacionales de los padres |
Variable compuesta de 6 ítems. Hace referencia, desde la mirada de los padres, al nivel educativo que creen que alcanzará el estudiante. Ejemplo: “No creo que complete IV año de educación Media” |
35,66% |
Expectativas educacionales de los estudiantes |
Variable compuesta de 4 ítems. Hace referencia al nivel educativo que los mismos estudiantes creen que alcanzarán. Ejemplo: “Completaré una carrera en una Universidad” |
6,63% |
Violencia escolar percibida por los padres |
Variable compuesta de 6 ítems con respuestas en escala Likert (cuatro tipos de niveles de acuerdo). Hace referencia a la frecuencia de situaciones de agresión en el establecimiento a partir de la experiencia e información que tienen los padres. Ejemplo: “Robos dentro del establecimiento” |
4,86% |
Número de libros en el hogar |
Variable compuesta por 5 ítems, referente al total de libros que se disponen en casa, exceptuando textos escolares, diarios o revistas. Ejemplo: “Entre 50 y 100” |
0,04% |
Fuente: Elaboración propia en base a
Cuestionarios de Contexto SIMCE 2015.
A partir de la Tabla II, se puede observar que autoeficacia en Matemática y expectativas educacionales de los padres contribuyen con un 88,47% a explicar los perfiles académicos de los estudiantes. La expectativa educacional de los padres se encuentra muy por sobre la propia expectativa educacional de los estudiantes, estableciendo una diferencia de 29,03% referente al porcentaje de contribución. La violencia escolar percibida por los padres contribuye en un 4,86%, lo cual hace mención de que ciertos perfiles guardan relación con esta variable. Lo mismo sucede con la variable números de libros en el hogar, que pese a contribuir en un 0,04%, el modelo arrojó que dicha variable es importante respecto a su aporte en ciertos perfiles académicos. Ésta última, corresponde a la variable con menor contribución.
El porcentaje de varianza explicada por el modelo CART fue de 25,3% y el RMSE fue de 54.16, lo que es educacionalmente relevante (Abdullah, Doucouliagos & Manning, 2013).
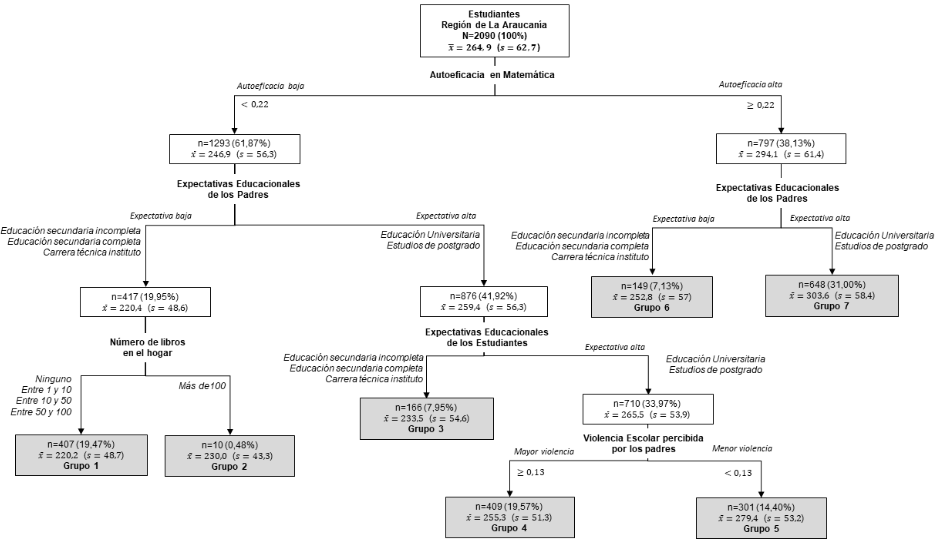
En cada nodo terminal o grupo terminal (en adelante G1, G2…G7), el valor superior indica la cantidad de estudiantes, luego el puntaje promedio en la prueba y finalmente la desviación estándar. En la Figura 2 se aprecia que el nodo raíz agrupa a toda la muestra de estudiantes, con 2.090 estudiantes de La Araucanía que obtuvieron en promedio 264.9 puntos en la prueba de Matemática. El nodo raíz fue dividido por la variable autoeficacia en Matemática en dos nodos hijos que forman las ramas izquierda y derecha del árbol de clasificación.
El nodo hijo del lado izquierdo del árbol comprende autoeficacia baja en Matemática agrupa a 1.293 estudiantes (61,87% de la muestra). Se presenta interacción entre autoeficacia en Matemática, expectativas de padres y estudiantes y número de libros en el hogar, dando origen a los cinco primero nodos o grupos terminales. La rama del lado derecho del árbol presenta autoeficacia alta en Matemática agrupa a 797 estudiantes (38,13% de la muestra). Se presenta interacción entre autoeficacia alta en Matemática, expectativas de padres y estudiantes y violencia escolar, dando origen a los grupos terminales 6 y 7. Ver Tabla III con indicadores de resumen.
Figura 2
Árbol de regresión de desempeño
en SIMCE Matemática 2015.
-----
Tabla 3
Indicadores de resumen de los
perfiles de desempeño en Matemática
|
G1 |
G2 |
G3 |
G4 |
G5 |
G6 |
G7 |
n |
407 |
10 |
166 |
409 |
301 |
149 |
648 |
Promedio |
220.2 |
230 |
233.5 |
255.3 |
279.4 |
252.8 |
303.6 |
Percentil |
49 |
49.6 |
51.6 |
50.9 |
55 |
51 |
56 |
Mínimo |
86.9 |
159.2 |
99.7 |
113.9 |
112.3 |
90.8 |
117.3 |
Desv.Est. |
48.7 |
43.3 |
54.6 |
51.3 |
53.2 |
57 |
58.4 |
Mediana |
222.4 |
235.1 |
238.2 |
256 |
288.2 |
256.2 |
313.8 |
5% |
135.3 |
159.2 |
139.3 |
167.9 |
177.7 |
159.8 |
202.2 |
25% |
186.4 |
196.8 |
192 |
221.9 |
245.5 |
214.5 |
265.6 |
75% |
252.5 |
257.4 |
272.7 |
289.8 |
317.9 |
286.6 |
345.8 |
95% |
302.2 |
301.7 |
322.9 |
332.8 |
356.6 |
349.3 |
390.6 |
Máximo |
362.5 |
301.7 |
348.3 |
418.3 |
405 |
405 |
422 |
La autoeficacia en Matemática generó el primer corte del árbol de rendimiento, en donde la rama izquierda representa aquellos perfiles en los cuales existe un nivel de autoeficacia en Matemática bajo y que se muestra como característico de cinco de los siete grupos terminales. Cabe mencionar que en la rama izquierda se presentan los dos perfiles con menores rendimientos (G1 y G2).
De los cinco grupos terminales con autoeficacia baja en Matemática, G1, G2, G3 y G4 se encuentran por debajo de la media muestral y solo G5 se encuentra por sobre los 264.9 puntos. En general, los 992 estudiantes (47,4% de la muestra) pertenecientes a los grupos G1, G2, G3 y G4 atribuyen sus dificultades en Matemática a la incapacidad de aprender, la falta de conocimiento o el esfuerzo mínimo (Bandura, 1994). La habilidad para resolver problemas es menor que la de los estudiantes que presentan altos niveles de autoeficacia en Matemática, debido a que los desafíos que se les presentan en su aprendizaje de la asignatura son considerados como amenazas para estos. Por el contrario, la rama derecha del árbol identifica a los estudiantes que presentan altos niveles de autoeficacia en Matemática, esto es, estudiantes que consideran los desafíos como oportunidades y por ello, se muestran más confiados y seguros de su actuar, aun cuando eso signifique cometer un error, pues demuestran mayor autonomía a la hora de responder frente a una situación planteada (Bandura, 1994).
Con relación a la comprensión de la interacción entre los factores familiares y características individuales de los estudiantes, las expectativas educacionales de los padres y expectativas educacionales de los estudiantes en el desempeño académico en Matemática el análisis arrojó que ambos factores contribuyen en su conjunto con un 42,29% del puntaje obtenido respecto del rendimiento académico en la asignatura de Matemática. El rol es tan importante que la expectativa educacional de los padres genera el segundo corte del árbol tanto para los nodos de bajo y alto nivel de autoeficacia en Matemática. Las expectativas de los padres y de los estudiantes acerca de sí mismos, se relacionan con el compromiso, comunicación y apoyo que desde el hogar se brinda al estudiante. Para esta investigación, las expectativas de los padres tienen hasta mayor peso que la misma expectativa de los estudiantes. Esto se explica de acuerdo a la literatura porque la participación activa de los padres y su rol fundamental y crítico en el desarrollo social y cognitivo de sus hijos presenta una relación positiva con el compromiso que asume el estudiante con sus labores escolares (Bravo et al., 2017) y en la clase de Matemática (Din, Ayub & Tarmizi, 2016).
Lo anterior no significa que, si los padres declaran altas expectativas, la expectativa de los estudiantes también lo sea. Así se puede notar para G3 que, aun teniendo altas expectativas de sus padres, los estudiantes declaran bajas expectativas educacionales, bajo nivel de autoeficacia en Matemática y presentan un menor rendimiento con diferencias de 32 puntos respecto del grupo G4, lo que sugiere que las expectativas educacionales de los padres deben estar acompañadas de comportamientos y acciones focalizadas que propendan tanto a fortalecer la emocionalidad y la autoeficacia en sus hijos e hijas, cumpliendo la escuela un rol clave a través de estrategias como una escuela para padres, de ahí el valor de poder visualizar el rol de las interacciones entre las variables contextuales e individuales.
Lo expresado antes, se evidencia más claramente en la rama izquierda donde se destacan los grupos G1 y G2 por tener los menores puntajes promedio, además, ambos grupos presentan bajos niveles de autoeficacia en Matemática y bajas expectativas educacionales de los padres, estableciendo una diferencia de 83 puntos con respecto al G7 que muestra altos niveles de autoeficacia en Matemática y altas expectativas educacionales de los padres. En la rama derecha del árbol, esto es, estudiantes con altos niveles de autoeficacia en Matemática, existe una diferencia de 51 puntos entre el grupo que declara bajas expectativas educacionales de los padres (G6) y altas expectativas educacionales de los padres (G7).
El grupo de estudiantes con altos niveles de autoeficacia en Matemática, pero con expectativas bajas de los padres (G6) tiene un rendimiento, en promedio, menor con una diferencia de 51 puntos respecto del grupo de estudiantes (G7) que declara altos niveles de autoeficacia en Matemáticas y altas expectativas educacionales de los padres, lo que sugiere el valor crítico que podría tener el modelamiento del acompañamiento parental en comportamientos autoeficaces y el desarrollo de una alta creencia en sí mismo. En este último punto, se evidencia con aquellos estudiantes que presentan bajas expectativas de sí mismo y presentan un rendimiento en promedio menor que quienes declaran altas expectativas, con una diferencia de 24 puntos entre ambos grupos (G4 y G5). Este último hallazgo sugiere una intervención más dirigida de los profesores para trabajar en conjunto con los padres con el fin de elevar sus expectativas educacionales respecto de sus hijos. Así también, el trabajo en clases de orientación u otros espacios educativos que promuevan el desarrollo de altas expectativas educacionales.
Respecto a la comprensión de factores de contexto escolar, como lo fue en este estudio la violencia escolar percibida por los padres en el desempeño académico en Matemática, la literatura muestra que en escuelas donde los niveles de violencia son bajos, enfatizando el rol de los profesores (Valdés-Cuervo, Martínez-Ferrer & Carlos-Martínez, 2017), éstas se correlacionan con climas positivos. Por tanto, promueven mejores ambientes de aprendizaje que conllevan resultados más óptimos para los colegios, mayor satisfacción a nivel familiar y personal para el estudiante (López, Bilbao y Rodríguez, 2012; Benbenishty et al., 2016). Además de lo anterior, la literatura señala que el trabajo con los apoderados y familiares de los estudiantes se relaciona con niveles de violencia escolar menores. Altos niveles de violencia conducen a desarrollar una menor autoestima y mayores niveles de soledad, lo cual repercute en las relaciones interpersonales y rendimientos académicos menores (Varela, Ávila y Martínez, 2013; Yupanqui et al., 2016).
Finalmente, el factor de contexto familiar que para esta investigación fue el número de libros en el hogar, contribuyó con el desempeño académico en Matemática con un 0,04%, colaborando en la configuración de los grupos terminales 1 y 2, diferenciándose ambos grupos en 10 puntos, siendo el de mejor rendimiento aquel grupo que cuenta con más de 100 ejemplares de lectura, textos educativos, libros culturales, entre otros. Aunque su contribución es muy baja, el resultado anterior coincide con la literatura en investigación educacional y en este caso, esta diferencia es relevante si consideramos que ambos grupos corresponden a los que presentan los menores rendimientos, baja autoeficacia y bajas expectativas educacionales de padres, lo que sugiere que especialmente para estos grupos contar con intervenciones educativas que promuevan el uso de los libros en el hogar y en la escuela es positivo, especialmente al realizarse desde los niveles educativos más tempranos.
A partir de la investigación, los resultados permiten suponer que aumentar las expectativas, desarrollar la autoeficacia y mejorar el ambiente escolar contribuirá en mejores desempeños en Matemática. Lo anterior sugiere, por una parte, incorporar en la formación inicial docente y formación continua una mirada integral y multidimensional de estos factores que intervienen en el desempeño académico, principalmente considerando la emergencia de variables relacionadas con el ambiente escolar y, por otra, fortalecer la relación familia-escuela a partir de su interacción y recíproca influencia, promoviendo su mayor participación en la comunidad educativa, especialmente en el contexto latinoamericano en que la política pública de participación de la familia-escuela es reciente (UNESCO, 2000).
Este estudio tuvo por objetivo obtener perfiles de desempeño a través de los factores que inciden en el rendimiento académico de Matemática, en una muestra representativa regional de estudiantes de secundaria en La Araucanía, Chile. Los análisis con RF y CART, identificaron siete perfiles de estudiantes según su rendimiento en Matemática, los cuales fueron descritos en función de las variables antes mencionadas, pudiendo apreciarse cómo factores de contexto familiar, escolar e individual interactúan e influencian el desempeño en Matemática con niveles diferentes de contribución.
Desde esta perspectiva, este estudio evidenció que el rol que cumple la autoeficacia en Matemática en el rendimiento académico es muy relevante. La contribución de esta variable al nivel observado del puntaje corresponde a un 52,81%, demostrando una importancia crítica en el desempeño de los estudiantes, confirmando lo mencionado por otras investigaciones en el área. Además, las expectativas educacionales de padres y estudiantes y, como factor de clima social escolar, la violencia percibida por los padres, son factores importantes a ser considerados de manera integral para aumentar los logros de aprendizaje en el dominio.
Esta investigación se ha realizado dentro del proyecto 11150665 subvencionado por FONDECYT-INICIACION, CONICYT.
Abdullah, A., Doucouliagos, H., y Manning, E. (2013). Does education reduce income inequality? a meta-regression analysis Journal of Economic Surveys (29)2, 301-316. https://doi.org/10.1111/joes.12056
Ahn, H. S., Usher, E. L., Butz, A., y Bong, M. (2016). Cultural differences in the understanding of modelling and feedback as sources of self‐efficacy information. British Journal of Educational Psychology, 86(1), 112-136. https://doi.org/10.1111/bjep.12093
Akgul, G., Cokamay, G., y Demir, E. (2016). Predictors of Teacher Support: Turkey and Shanghai in the Programme for International Student Assessment, 2012. Eurasian Journal of Educational Research, 63, 115-132. https://doi.org/10.14689/ejer.2016.63.7
Akiba, M., Shimizu, K., y Zhuang, Y. (2010). Bullies, Victims, and Teachers in Japanese Middle Schools. Comparative Education Review, 54(3), 369–392. https://doi.org/10.1086/653142
Bandura, A. (1977). Self-efficacy: toward a unifying theory of behavioral change. Psychological review, 84(2), 191. https://doi.org/10.1016/0146-6402(78)90002-4
Bandura, A. (1994). Self-efficacy. In V. S. Ramachaudran (Ed.), Encyclopedia of human behavior (Vol. 4, pp. 71-81). New York: Academic Press. (Reprinted in H. Friedman [Ed.], Encyclopedia of mental health. San Diego: Academic Press, 1998).
Bandura, A. (2002). Social cognitive theory in cultural context. Applied psychology, 51(2), 269-290. https://doi.org/10.1111/1464-0597.00092
Benbenishty, R., Astor, R. A., Roziner, I., y Wrabel, S. L. (2016). Testing the causal links between school climate, school violence, and school academic performance: A cross-lagged panel autoregressive model. Educational Researcher, 45(3), 197-206. https://doi.org/10.3102/0013189X16644603
Berger, C., Álamos, P., Milicic, N., y Alcalay, L. (2014). Rendimiento académico y las dimensiones personal y contextual del aprendizaje socioemocional: Evidencias de su asociación en estudiantes chilenos. Universitas Psychologica, 13(2), 627-638. http://dx.doi.org/10.11144/Javeriana.UPSY13-2.radp.
Bourdieu, P. (1979). Los tres estados del capital cultural. Trad. M., Landesmann. Sociológica, 5, 11–17. Recuperado de https://sociologiac.net/biblio/Bourdieu-LosTresEstadosdelCapitalCultural.pdf
Bravo-Sanzana, M., Salvo, S., y Mieres-Chacaltana, M. (2015). La importancia de la salud emocional en la escuela, un factor a considerar para la mejora de la salud mental y los logros en el aprendizaje. Salud Pública Méx, 57(5), 321–322. Recuperado de http://www.saludpublica.mx/index.php/spm/article/view/7406/10334
Bravo-Sanzana, M., Salvo, S., y Muñoz, C. (2015). Profiles of Chilean students according to academic performance in mathematics: An exploratory study using classification trees and random forests. Studies in Educational Evaluation, 44, 50-59. https://doi.org/10.1016/j.stueduc.2015.01.002
Bravo-Sanzana, M., Salvo, S., y Mieres-Chacaltana, M. (2016). El clima social escolar en el logro de aprendizajes y el desarrollo integral, ¿cómo afecta a la salud mental de los niños y niñas? Salud Pública Méx, 58(6), 597–600. https://doi.org/10.21149/spm.v58i6.7913
Bravo, M., Salvo, S. y Mieres, M., Mansilla, J. y Hederich, C. (2017). Perfiles de desempeño académico: la importancia de las expectativas familiares. Perfiles Latinoamericanos, (25) 50. http://dx.doi.org/10.18504/pl2550-016-2017
Breiman, L., Friedman, J., Stone, C. J., y Olshen, R. A. (1984). Classification and regression trees. CRC press.
Bronfenbrenner, U. (1987). La ecología del desarrollo humano. Buenos Aires: Paidós.
Browne, M. W., & Cudeck, R. (1993). Alternative Ways of Assessing Model Fit. In: K. A. Bollen, & J. S. Long (Eds.), Testing Structural Equation Models (pp. 136-162). Beverly Hills, CA: Sage.
Çengel, M., y Türkoğlu, A. (2016). Analysis through hidden curriculum of peer relations in two different classes with positive and negative classroom climates. Educational Sciences: Theory y Practice, 16, 1893–1919. https://doi.org/10.12738/estp.2016.6.0103
Cetin, S., y Gok, B. (2017). Modeling the Factors Affecting Students' Mathematical Literacy Scores: The Case of PISA 2012. Hacettepe Üniversitesi Eğitim Fakültesi Dergisin, 32(4), 982-998. https://doi.org/10.16986/HUJE.2016023162
Chaparro, A., González, C., y Caso, J. (2016). Familia y rendimiento académico: configuración de perfiles estudiantiles en secundaria. Revista Electrónica de Investigación Educativa, 18(1), 53–68. Recuperado de https://redie.uabc.mx/redie/article/view/774
Claro, J. (2013). Calidad en educación y clima escolar: apuntes generales. Estudios Pedagógicos, 39(1), 347–359. https://doi.org/10.4067/S0718-07052013000100020
Din, N. M., Ayub, A. F. M., y Tarmizi, R. A. (2016). Influence of Parental Involvement and Peer Support on Mathematics Engagement Among Malaysian Secondary School Students. Malaysian Journal of Mathematical Sciences, 10, 175-185. Recuperado de http://einspem.upm.edu.my/journal/fullpaper/vol10saugust/13.%20Norakusuma.pdf
Doménech-Betoret, F., Abellán-Roselló, L., y Gómez-Artiga, A. (2017). Self-Efficacy, Satisfaction, and Academic Achievement: The Mediator Role of Students' Expectancy-Value Beliefs. Frontiers in psychology, 8, 1193. https://doi:10.3389/fpsyg.2017.01193
Gamazo, A., Martínez-Abad, F., Olmos-Migueláñez, S., & Rodríguez-Conde, M. J. (2018). Evaluación de factores relacionados con la eficacia escolar en PISA 2015. Un análisis multinivel. Revista de Educación, (379), 52–78. https://doi.org/10.4438/1988-592X-RE-2017-379-369
Garbacz, S. A., Herman, K. C., Thompson, A. M., y Reinke, W. M. (2017). Family engagement in education and intervention: Implementation and evaluation to maximize family, school, and student outcomes. Journal of School Psychology, 62, 1-10. https://doi.org/10.1016/j.jsp.2017.04.002
Henning, C., Cuesta, L., Fernández, O., y Dorival, F. (2018). Cyberbullying, detección y factores de análisis: Un estudio comparativo. Revista Espacios. 40(2), 4. Recuperado de: https://www.revistaespacios.com/a19v40n02/a19v40n02p04.pdf
Jöreskog, K. G. (1994). On the estimation of polychorics correlations and their asymptotic covariance matrix. Psychometrika, 59(3), 381–389. https://doi.org/10.1007/BF02296131
Kamalimoghaddam, H., Tarmizi, R. A., Ayub, A. F. M., y Jaafar, W. M. W. (2016). Confirmatory Model of Mathematics Self-Efficacy, Problem Solving Skills and Prior Knowledge on Mathematics Achievement: A Structural Equation Model. Malaysian Journal of Mathematical Sciences, 10, 187-200. Recuperado de http://psasir.upm.edu.my/id/eprint/52374
Kogar, H. (2015). Examination of factors affecting PISA 2012 mathematical literacy through mediation model. Egitim ve Bilim, 40(179). https://doi.org/10.15390/EB.2015.4445
Konold, T., Cornell, D., Shukla, K., y Huang, F. (2017). Racial/ethnic differences in perceptions of school climate and its association with student engagement and peer aggression. Journal of youth and adolescence, 46(6), 1289-1303. https://doi.org/10.1007/s10964-016-0576-1
Kumari, P., y Dhull, P. (2017). School Climate and student’s outcome. International Education and Research Journal, 3(3), 132–134. Recuperado de http://www.ijsre.com
López, V., Bilbao, M. D. L. A., y Rodriguez, J. I. (2012). La sala de clases sí importa: incidencia del clima de aula sobre la percepción de intimidación y victimización entre escolares. Universitas Psychologica, 11(1). https://doi.org/10.11144/Javeriana.upsy11-1.scii
López, M., Efstathios, S. y Herrera, M. (2018). Clima escolar y desempeño docente: un caso de éxito. Aproximaciones a escuelas públicas de la provincia de Carchi-Ecuador. Revista Espacios. 39(35), 5. Recuperado de: https://www.revistaespacios.com/a18v39n35/a18v39n35p05.pdf
Ma, X., 2005. Growth in Mathematics Achievement: Analysis with Classification and Regression Trees. The Journal of Educational Research, 99 (2), 78-86. https://doi.org/10.3200/JOER.99.2.78-86
Martin, A. J., Way, J., Bobis, J., y Anderson, J. (2015). Exploring the ups and downs of mathematics engagement in the middle years of school. The Journal of Early Adolescence, 35(2), 199-244. https://doi.org/10.1177/0272431614529365
Martínez-Abad, F., Lizasoain, L., Castro, M., y Joaristi, L. (2017). Selección de escuelas de alta y baja eficacia en Baja California (México). Revista Electrónica de Investigación Educativa, 19(2), 38–53. https://doi.org/10.24320/redie.2017.19.2.960
MINEDUC. (2012). Informe Técnico SIMCE 2012. Agencia de Calidad de la Educación. Santiago de Chile: Ministerio de Educación de Chile. Recuperado de: http://archivos.agenciaeducacion.cl/documentos-web/Informe_Tecnico_Simce_2012.pdf.
MINEDUC. (2013). Calculo de significancia estadística para resultados de las pruebas SIMCE. Santiago Chile. Retrieved from http://archivos.agenciaeducacion.cl/Calculo-de-Significancia-Estadistica.pdf
MINEDUC. (2015). Resultados Educativos 2015. Santiago de Chile. Recuperado de http://archivos.agenciaeducacion.cl/Presentacion_resultados_educativos_8basico_IImedio_2015.pdf
MINEDUC. (2016a). Plan de aseguramiento de la calidad escolar 2016-2019. Santiago de Chile. Recuperado de https://www.supereduc.cl/wp-content/uploads/2016/12/Plan-de-Aseguramiento.pdf
MINEDUC. (2016b). Resultados Educativos 2016: IX Región de La Araucanía. Santiago Chile. Recuperado de http://archivos.agenciaeducacion.cl/PDFConferencia_ARAUCANIA_2016.pdf
MINEDUC. (2017). Resultados Educativos 2017. Región de La Araucanía. Santiago Chile. Recuperado de https://archivos.agenciaeducacion.cl/Region_de_La_Araucania_2017.pdf
Moratto, N., Cárdenas, N., y Berbesí, D. (2017). Clima escolar y funcionalidad familiar como factores asociados a la intimidación escolar en Antioquia, Colombia. Pensamiento Psicológico, 15 (1), 63-72. https://doi:10.11144/Javerianacali.PPSI15-1.CEFF
Murillo, F. J., y Garrido, C. M. (2017). Segregación Social En Las Escuelas Públicas Y Privadas En América Latina. Educação y Sociedade, (0), 727–750. https://doi.org/10.1590/es0101-73302017167714
Muthén, L. K., & Muthén, B. O. (1998-2012). Mplus User’s Guide: Statistical Analysis with Latent Variables (7th ed.). Los Angeles, CA: Muthén & Muthén.
Ng, C. C. (2018). High School Students’ Motivation to Learn Mathematics: The Role of Multiple Goals. International Journal of Science and Mathematics Education, 16(2), 357-375. https://doi.org/10.1007/s10763-016-9780-4
OCDE. (2016). Pisa 2015. Resultados claves. Recuperado de http://www.oecd.org/pisa/pisa-2015-results-in-focus-ESP.pdf
OREALC/UNESCO. (2015). Informe de resultados TERCE, Factores Asociados. Santiago de Chile. Recuperado de https://unesdoc.unesco.org/ark:/48223/pf0000243533
O'malley, M., Voight, A., Renshaw, T. L., y Eklund, K. (2015). School climate, family structure, and academic achievement: A study of moderation effects. School Psychology Quarterly, 30(1), https://doi.org/142. 10.1037/spq0000076.
Recber, S., Isiksal, M., y Koc, Y. (2017). Investigating self-efficacy, anxiety, attitudes and mathematics achievement regarding gender and school type. Anales de Psicología/Annals of Psychology, 34(1), 41-51. https://doi.org/10.6018/analesps.34.1.229571
Ruvalcaba-Romero, N. A., Gallegos-Guajardo, J., y Fuerte Nava, J. M. (2017). Competencias socioemocionales como predictoras de conductas prosociales y clima escolar positivo en adolescentes. Revista Interuniversitaria de Formación del Profesorado, 31(1), 77-90. Recuperado de https://www.redalyc.org/articulo.oa?id=27450136012
Rudasill, K. M., Snyder, K. E., Levinson, H., & Adelson, J. L. (2018). Systems View of School Climate: a Theoretical Framework for Research. Educ Psychol Rev, 30(1), 35–60. https://doi.org/10.1007/s10648-017-9401-y
Ruíz-Ramírez, R., García-Cué, J., Ruíz, F., y Ruíz, A. (2018). La relación bullying-deserción escolar en bachilleratos rurales. Revista Electrónica de Investigación Educativa, 20(2), 37–45. https://doi.org/10.24320/redie.2018.20.2.1527
Şahin, M. G., y Yıldırım, Y. (2016). The Examination of the Variables Affecting Mathematics Behavior and Mathematics Literacy by Multi-Group Hybrid Model in the Sample of PISA 2012 Turkey. Egitim ve Bilim, 41(187). https://doi.org/10.15390/EB.2016.6837
Serra-Olivares, J. (2016). Examinando las posibilidades del Modelo de Educación Deportiva sobre la convivencia escolar: Ejemplo en La Araucanía. Retos, 0(31), 227-231.
Scheaffer, R. L. R. L., Mendenhall, W., y Ott, L. (1987). Elementos de muestreo (No. 04; HA31. 2. M45, S2y.). Recuperado de https://recyt.fecyt.es/index.php/retos/article/view/49038/32161
Schumacher, R., y Lomax, R. (1996). A beginner’s guide to structural equation modeling. (L. Erlbaum, Ed.). New Jersey, NJ.
Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis. London: Monographs on Statistics and Applied Probability, School of Mathematics University of Bath, UK. Recuperado de https://ned.ipac.caltech.edu/level5/March02/Silverman/paper.pdf
Thien, L. M., y Ong, M. Y. (2015). Malaysian and Singaporean students’ affective characteristics and mathematics performance: evidence from PISA 2012. SpringerPlus, 4(1), 563. https://doi.org/10.1186/s40064-015-1358-z.
Tomopoulos, S., Dreyer, B., Tamis-LeMonda, C., Flynn, V., Rovira, I., Tineo, W., y Mendelsohn, A. (2006). Books, Toys, Parent-Child Interaction, and Development in Young Latino Children. Ambulatory Pediatrics, 6(2), 72–78. https://doi.org/10.1016/j.ambp.2005.10.001
Toro, I., y Parra, R. (2010). Fundamentos epistemológicos de la investigación y la metodología de la investigación cualitativa/cuantitativa. Medellín: Fondo Editorial Universidad EAFIT.
Tosto, M. G., Asbury, K., Mazzocco, M. M., Petrill, S. A., y Kovas, Y. (2016). From classroom environment to mathematics achievement: The mediating role of self-perceived ability and subject interest. Learning and individual differences, 50, 260-269. https://doi.org/10.1016/j.lindif.2016.07.009
Trucco, D., & Inostroza, P. (2017). Las violencias en el espacio escolar. Comisión Económica Para América Latina y El Caribe (CEPAL), 222–247. Recuperado de https://repositorio.cepal.org/bitstream/handle/11362/41068/1/S1700122_es.pdf
UNESCO: Educación para todos. Diez años después de Jomtien. Fuentes. N° 122. Abril 2000. Recuperado de http://unesdoc.unesco.org/images/0011/001195/119519s.pdf
Usta, H. G. (2016). Analysis of Student and School Level Variables Related to Mathematics Self-Efficacy Level Based on PISA 2012 Results for China-Shanghai, Turkey, and Greece. Educational Sciences: Theory and Practice, 16(4), 1297-1323. https://doi.org/10.12738/estp.2016.4.0283
Valdés-Cuervo, Á. A., Martínez-Ferrer, B., y Carlos-Martínez, E. A. (2017). El rol de las prácticas docentes en la prevención de la violencia escolar entre pares. Revista de Psicodidáctica, 22(2), 33-38. https://doi.org/10.1016/j.psicod.2017.05.006
Varela, R. M., Ávila, E., y Martínez, B. (2013). Violencia escolar: Un análisis desde los diferentes contextos de interacción. Psychosocial Intervention, 22(1), 25-32. http://dx.doi.org/10.5093/in2013a4
Vargas, G. I., Villarreal, H. M., Espitia, D., Piñeros, C., & Marín, D. A. (2018). Una mirada crítica a los manuales de convivencia escolar en diez (10) instituciones educativas del departamento del Tolima (Colombia) orientados a la solución de problemas. Revista Espacios, 39(40), 9. Recuperado de http://www.revistaespacios.com/a18v39n40/a18v39n40p09.pdf
Yu, R., y Singh, K. (2018). Teacher support, instructional practices, student motivation, and mathematics achievement in high school. The Journal of Educational Research, 111(1), 81-94. https://doi.org/10.1080/00220671.2016.1204260
Yupanqui, A., González, M., Llancalahuén, M., Quilodrán, W., y Toledo, C. (2016). Lenguaje, discriminación y discapacidad en el contexto educativo de Magallanes: Un enfoque de derechos humanos desde la terapia ocupacional. Magallania (Punta Arenas), 44(1), 149-166. http://dx.doi.org/10.4067/S0718-22442016000100009
Yurt, E. (2014). The predictive power of self-efficacy sources for mathematics achievement. Egitim Ve Bilim, 39(176). http://dx.doi.org/10.15390/EB.2014.3443
1. Universidad de La Frontera. Chile. monicaviviana.bravo@ufrontera.cl
2. Universidad de La Frontera. Chile. matias.pavez@ufrontera.cl
3. Universidad de La Frontera. sonia.salvo@ufrontera.cl
4. Universidad Católica de Temuco. Chile. mieres@uct.cl
5. https://www.jmp.com/es_mx/site/see-jmp.html