

 Vol. 40 (Number 29) Year 2019. Page 12
Vol. 40 (Number 29) Year 2019. Page 12
AUMGRI, Charinthorn 1 & PETSANGSRI, Sirirat 2
Received: 24/04/2019 • Approved: 13/08/2019 • Published 02/09/2019
ABSTRACT: This study aimed to develop computational thinking components for preservice teachers in Thai universities. Through multi-stage random sampling, the sample comprised 747 students enrolled in Computer Education at Rajabhat universities in Thailand. The instrument was a questionnaire with a 5-point rating scale; a range of item-objective congruence (IOC) between 0.80-1.00; and a reliability coefficient of 0.98. The data were analyzed using basic statistics and a second-order confirmatory factor analysis via LISREL. |
RESUMEN: Este estudio tuvo como objetivo desarrollar componentes de pensamiento computacional para maestros en servicio en universidades tailandesas. A través del muestreo aleatorio en varias etapas, la muestra comprendió a 747 estudiantes matriculados en Educación Informática en las universidades de Rajabhat en Tailandia. El instrumento era un cuestionario con una escala de calificación de 5 puntos; un rango de congruencia elemento-objetivo (COI) entre 0.80-1.00; y un coeficiente de fiabilidad de 0,98. Los datos se analizaron mediante estadísticas básicas y un análisis factorial confirmatorio de segundo orden a través de LISREL. |
In response to the dynamics of the 21st century, educational management should be revolved around the educational development concept of multidimensional thinking which focuses on skill sets such as life and work; learning and innovation; and information, media, and technology (Partnership for 21st Century Learning, 2009, p. 21; Panich, 2012, pp. 6-7). As reflected in many of its plans, Thailand is also known to have been implementing this educational paradigm. The National Economic and Social Development Plan focuses on creative thinking, innovations with enhanced economic values, and innovative extensions at local and macro levels that would positively impact life quality and foster necessary skills suitable with the 21st-century educational era (The Twelfth National Economic and Social Development Plan 2017-2021, 2015). In addition, the Educational Development Plan of the Ministry of Education requires educational institutions to develop curriculums, teaching processes, and educational personnel; expand accesses to educational services for lifelong learning; promote and develop information and communication technology systems for education; and develop a management system that promotes all-sector involvement in maneuvering education consistently with the 20-year Educational Development Plan (Ministry of Education, 2016).
Computational thinking (CT) is one of the subskills of “digital literacy” and an essential competency for 21st-century students. The skill is vital as it gives an individual the ability to distinguish and summarize the needed data out of the vast sources. Procedurally, the data are processed, broken down into comprehensible chunks, and fed into some technological solutions to solve the problems. In some complex cases, customized programs could be developed to facilitate computing tasks or management processes. Computational thinking is not a skill exclusively tied to Computer Science. In fact, it is a fundamental skill associated with logic, analyzing, and problem-solving which is deemed beneficial for learning, working, and sustaining a daily life (Wing, 2006, pp. 33-35; IFTF, 2011; Cuny et al., 2010). Its components comprise selecting usable data, determining problem-solving processes; designing systematic problem-solving sequences; working effectively in collaboration; evaluating outcomes; creating workpieces; and resolving mistakes (Lye & Koh, 2014; Swaid, 2015; Zhong et al., 2016).
The production of teachers in Thailand is carried out by public and private universities. Rajabhat universities have been among the public institutions in charge of this role for over 90 years and along with its continued production of computer teachers (History of Rajabhat University, 2019; Piatanom, 2008). UNESCO (2008) indicates that computer teachers should acquire professionally necessary knowledge, skills, and competencies to manage information-technology education. Consistently, Teachers and Basic Education Personnel Development Bureau (2010) backs the notion by supporting the teachers’ ability to use and develop innovative media in their educational management. Consequently, this study scoped its examination to the teaching managements for students enrolled in Computer Education throughout Rajabhat universities in Thailand as the findings were projected to produce the discoveries that could be practically implemented in teaching. During the next phase of the study, a STEM teaching integrated with an engineering design will be developed for undergraduate students to enhance computational thinking.
To analyze computational thinking components for preservice teachers in Thailand.
According to Wing (2006), Cuny (2010), Stephenson (2011), Ornduff (2012), Brennan & Resnick (2012), Lye & Koh (2014), Swaid (2015), Zhong et al. (2016), Gonzalez et al. (2017), and Basogain et al. (2017) computational thinking refers to a person’s capacity to analytically select data from recurring problems; determine problem solving processes; design problem-solving sequences; evaluate outcomes; resolve mistakes; create workpieces; and work in collaboration. The term contains seven components including the ability to determine problem-solving processes; the ability to design problem-solving sequences; the ability to evaluate outcomes; the ability to resolve mistakes; the ability to work in collaboration; and the ability to create workpieces. The skill can be effectively used in learning, thinking, analyzing, designing, developing, problem-solving, evaluating, workpieces making, and systematic computer collaboration. As Perevoshchikova et al. (2018) describes, it could solve problems in the experimental procedures as it predicted learning behaviors. Congruently with Pluzhnikova et al. (2018), the skill helps individuals comprehend complex knowledge. Also, Teixeira Monteiro (2017) indicates that computational thinking is fundamental in Software Engineering and it can support the learning through theoretical and practical concepts (Valencia et al., 2016). The notion is in line with Rabiee & Tjoa (2017) stating that it is a practical solution for real-life problems, and it can integrate physical and virtual teaching (Daily et al., 2014). In addition, Allsop (2019) employs metacognitive practices, learning behaviors, and computational concepts whereas, Paula et al. (2018) believes that computational thinking is a viable problem-solving skill and concept in the 21st century, especially when interacting with digital technologies and different knowledge disciplines, e.g., Arts and Humanities or STEM (CT); or bridging together the two areas in schooling.
Confirmatory factor analysis is a test of hypothesis to determine variables within component constructs, investigate the factor loadings or correlations of the variables to such components, and interpret whether the results match the predetermined forecasts. The procedure begins with the creation of a hypothesis based on the data obtained from population observations. As the data contain some common components which create the relationship between normally distributed data, confirmatory factor analysis can quantify the components of the studied variables. The advantages of this analytical method are, firstly, it can minimize the number of variables required to structurally validate the variables, secondly, it can analyze the relationship structures of various variables within the same factor, thirdly, it can define or classify each component, and fourthly, it can be effectively used in planning, i.e., measuring, verifying a hypothesis, discovering unknown components, and systematically identifying concepts and sources of variability (Mueller, 1996; Marsh et al., 1998; Bollen & Long, 1983; Aroian & Norris, 2001; Kenny & McCoach, 2003; Mejang, 2014, pp. 28-33)
The population was 6,434 undergraduate students in Computer Education from faculties of education of 38 Rajabhat universities in Thailand (Office of Higher Education, 2017). The sample size was determined based on Hair et al. (2010) proposing that the ratio between the sample units and the observed variables should be at least 20:1. Since there were 25 observed variables in this study, the appropriate and adequate sample size was to be at least 480. To ensure the reliability of the hypothesis testing, this study employed a multi-stage random sampling (i.e., cluster- and simple-random samplings) to select 785 samples.
Table 1
Student samples by sex and region
Geographic Region |
Sex |
Quantity |
|
Population |
Sample |
||
North |
Male |
250 |
61 |
Female |
268 |
63 |
|
Total |
518 |
124 |
|
South |
Male |
191 |
49 |
Female |
389 |
67 |
|
Total |
580 |
116 |
|
Central |
Male |
786 |
88 |
|
Female |
996 |
107 |
|
Total |
1,782 |
195 |
Northeast |
Male |
1,272 |
179 |
|
Female |
1,178 |
171 |
|
Total |
2,838 |
350 |
Total |
Male |
2,499 |
377 |
Female |
2,831 |
408 |
|
Total |
5,718 |
785 |
|
The instrument was a student questionnaire on computational thinking which has a 5-point rating scale, 7 main components, 25 subcomponents, and 25 questions/indicators. The questionnaire was validated by 7 experts who are university lecturers in Computer Education, and the validation indicated a range of item-objective congruence (IOC) between 0.70-1.00. The questionnaire was pilot-tested with 30 non-sampled undergraduate students of the same population and demonstrated a reliability coefficient of 0.98.
The data were collected from the samples during September to December 2018 through either coordination with a research network or an appointment with a lecturer of a sample. The researcher, then, personally or electronically delivered the questionnaire. Initially, 688 completed questionnaire responses (87.64%) were returned. Later, the researcher approached the respondents and managed to obtain the rest of the responses.
The data were analyzed using LISREL’s second-order confirmatory factor analysis using the Goodness of Fit Statistics as elaborated in Table 2.
Table 2
Skewness and Kurtosis of latent and observed variables
Observed Variables |
Number of items |
a |
M |
SD. |
Skew |
Kurt |
The ability to analyze and manage data (A) |
||||||
The ability to analyze and manage information from an occurred problem (y1) |
4 |
0.97 |
3.99 |
0.84 |
-0.23 |
-0.97 |
The ability to search for information from an occurred problem (y2) |
4 |
0.96 |
3.98 |
0.86 |
-0.39 |
-0.58 |
The ability to categorize information from an occurred problem (y3) |
4 |
0.96 |
3.88 |
0.82 |
-0.21 |
-0.54 |
The ability to select information from an occurred problem (y4) |
4 |
0.97 |
3.97 |
0.89 |
-0.67 |
0.38 |
The ability to use the information to solve problems (B) |
||||||
The ability to collect necessary information for the problem-solving (y5) |
3 |
0.97 |
4.05 |
0.84 |
-0.58 |
-0.17 |
The ability to store information for the problem-solving (y6) |
3 |
0.96 |
4.02 |
0.84 |
-0.66 |
.42 |
The ability to summarize information for the problem-solving (y7) |
3 |
0.96 |
4.08 |
0.89 |
-0.69 |
.084 |
The ability to design countermeasures (C) |
||||||
The ability to distinguish countermeasures (y8) |
4 |
0.96 |
4.01 |
0.88 |
-0.75 |
0.66 |
The ability to synthesize a countermeasure (y9) |
4 |
0.96 |
4.03 |
0.86 |
-0.71 |
0.45 |
The ability to design a countermeasure (y10) |
4 |
0.96 |
4.01 |
0.85 |
-0.60 |
0.23 |
The ability to formulate a problem-solving sequence (y11) |
4 |
0.96 |
3.99 |
0.88 |
-0.61 |
0.15 |
The ability to create workpieces (D) |
||||||
The ability to create a workpiece through self-learning (y12) |
4 |
0.96 |
4.16 |
0.84 |
-0.82 |
0.51 |
The ability to create a workpiece from others' suggestions (y13) |
4 |
0.96 |
4.04 |
0.87 |
-0.72 |
0.43 |
The ability to complete the overall production (y14) |
4 |
0.96 |
4.12 |
0.84 |
-0.54 |
-0.53 |
The ability to extend the work beyond the completed production (y15) |
4 |
0.96 |
4.16 |
0.85 |
-0.77 |
0.23 |
The ability to evaluate workpieces (E) |
||||||
The ability to plan a production (y16) |
4 |
0.96 |
3.99 |
0.80 |
-0.32 |
-0.51 |
The ability to follow procedures to create a workpiece (y17) |
4 |
0.96 |
3.96 |
0.81 |
-0.51 |
0.30 |
The ability to summarize the production results (y18) |
4 |
0.96 |
4.00 |
0.85 |
-0.53 |
0.08 |
The ability to present the produced workpiece (y19) |
4 |
0.97 |
3.97 |
0.86 |
-0.47 |
-0.01 |
The ability to analytically identify causes (F) |
||||||
The ability to identify causes of mistakes of the produced workpiece (y20) |
3 |
0.96 |
4.14 |
0.85 |
-0.75 |
.26 |
The ability to remediate the mistakes of the produced workpiece (y21) |
3 |
0.96 |
4.14 |
0.85 |
-0.62 |
-0.50 |
The ability to extensively develop the remedy for the mistakes of the produced workpiece (y22) |
3 |
0.96 |
4.19 |
0.82 |
-0.60 |
-0.55 |
The ability to work in collaboration (G) |
||||||
The ability to communicate during a collaboration (y23) |
3 |
0.96 |
3.94 |
0.82 |
-0.35 |
-0.38 |
The ability to cooperate during a collaboration (y24) |
3 |
0.97 |
3.92 |
0.80 |
-0.29 |
-0.30 |
The ability to exchange knowledge during a collaboration (y25) |
3 |
0.96 |
4.05 |
0.85 |
-0.42 |
-0.58 |
*Skewness < |1| (Hair, & et al. 2014)
** Kurtosis < |7| (Curran, & et al. 1996)
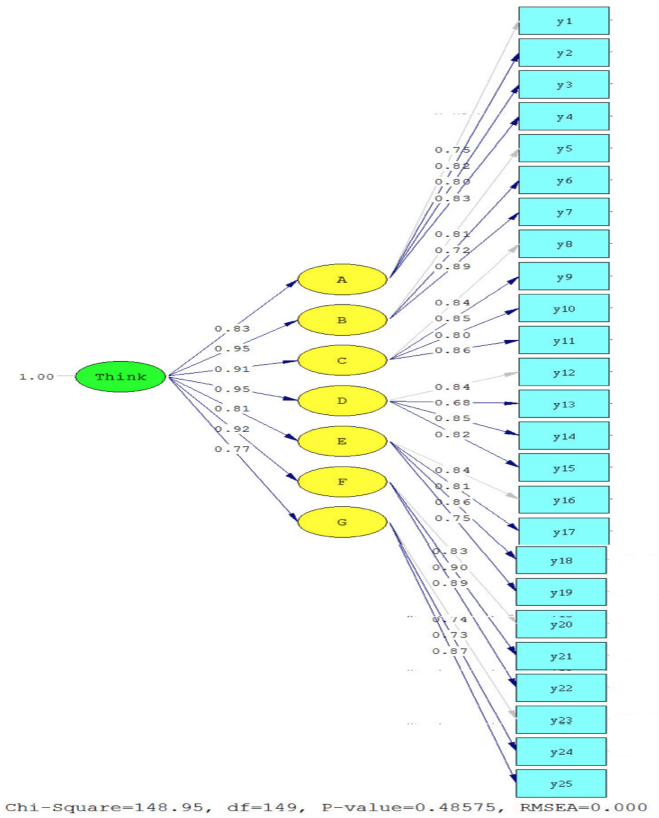
The second-order confirmatory factor analysis of computational thinking among the university students in Thailand produced the results as demonstrated in Table 3-4 and as summarized in Figure 1.
Figure 1
Second-order CFA model of computational
thinking among university students
-----
Table 3
Criteria and theory of the values
of Goodness-of-Fit Appraisal
Criteria Index |
Criteria |
Values |
Results |
Supporting theory |
Chi-square: χ2 |
p ≥ 0.05 |
0.48 |
passed |
Rasch, 1980 |
Relative Chi-square: χ2/df |
≤ 2.00 |
0.99 |
passed |
Byrne et al.,1989 |
RMSEA |
≤ 0.05 |
0.00 |
passed |
Hu & Bentler, 1999. |
GFI |
≥ 0.90 |
0.98 |
passed |
Jöreskog et al., 2016. |
AGFI |
≥ 0.90 |
0.96 |
passed |
Hooper et al., 2008 |
RMR |
≤ 0.05 |
0.02 |
passed |
Hu & Bentler, 1999 |
SRMR |
≤ 0.05 |
0.02 |
passed |
Hu & Bentler, 1999 |
NFI |
≥ 0.90 |
1.00 |
passed |
Schumacker & Lomax, 2010 |
CFI |
≥ 0.90 |
1.00 |
passed |
Schumacker & Lomax, 2010 |
Chi-Square = 148.95, df = 149, P = 0.49, c2 /df = 0.999, RMSEA = 0.00,
RMR = 0.0194, GFI = 0.985, AGFI = 0.967, PGFI = 0.452, CFI = 1.00
-----
Table 4
Correlation coefficient between latent variables (under the diagonal),
construct reliability (rC), and average variance extracted (AVE)
Latent Variables |
A |
B |
C |
D |
E |
F |
G |
A |
1 |
|
|
|
|
|
|
B |
0.79** |
1 |
|
|
|
|
|
C |
0.75** |
0.86** |
1 |
|
|
|
|
D |
0.78** |
0.90** |
0.86** |
1 |
|
|
|
E |
0.67** |
0.77** |
0.74** |
0.77** |
1 |
|
|
F |
0.76** |
0.87** |
0.83** |
0.87** |
0.75** |
1 |
|
G |
0.64** |
0.74** |
0.70** |
0.73** |
0.63** |
0.71** |
1 |
rV (AVE) |
0.64 |
0.66 |
0.70 |
0.64 |
0.67 |
0.76 |
0.61 |
rC (Construct Reliability) |
0.88 |
0.85 |
0.90 |
0.88 |
0.87 |
0.91 |
0.82 |
|
0.80 |
0.81 |
0.84 |
0.80 |
0.82 |
0.87 |
0.78 |
**Sig. < .01
-----
Table 5
The second-order confirmatory factor analysis of computational
thinking among the preservice teachers in Thailand
Variables |
Factor Loadings |
|||
bsc |
S.E. |
t (C.R) |
R2 |
|
The ability to analyze and manage data (A) |
0.83 |
0.04 |
20.26** |
0.69 |
The ability to analyze and manage information from an occurred problem (y1) |
0.75 |
< - > |
< - > |
0.57 |
The ability to search for information from an occurred problem (y2) |
0.82 |
0.03 |
24.85** |
0.68 |
The ability to categorize information from an occurred problem (y3) |
0.80 |
0.04 |
22.33** |
0.64 |
The ability to select information from an occurred problem (y4) |
0.83 |
0.04 |
22.98** |
0.69 |
The ability to use the information to solve problems (B) |
0.95 |
0.04 |
24.68** |
0.90 |
The ability to collect necessary information for the problem-solving (y5) |
0.81 |
< - > |
< - > |
0.67 |
The ability to store information for the problem-solving (y6) |
0.72 |
0.03 |
23.71** |
0.52 |
The ability to summarize information for the problem-solving (y7) |
0.89 |
0.04 |
24.75** |
0.80 |
The ability to design countermeasures (C) |
0.91 |
0.04 |
25.15** |
0.82 |
The ability to distinguish countermeasures (y8) |
0.84 |
< - > |
< - > |
0.70 |
The ability to synthesize a countermeasure (y9) |
0.85 |
0.03 |
29.06** |
0.72 |
The ability to design a countermeasure (y10) |
0.79 |
0.03 |
27.01** |
0.64 |
The ability to formulate a problem-solving sequence (y11) |
0.86 |
0.03 |
29.81** |
0.75 |
The ability to create workpieces (D) |
0.95 |
0.04 |
26.55** |
0.90 |
The ability to create a workpiece through self-learning (y12) |
0.84 |
< - > |
< - > |
0.70 |
The ability to create a workpiece from others' suggestions (y13) |
0.68 |
0.03 |
21.43** |
0.47 |
The ability to complete the overall production (y14) |
0.85 |
0.03 |
29.15** |
0.72 |
The ability to extend the work beyond the completed production (y15) |
0.82 |
0.03 |
27.65** |
0.68 |
The ability to evaluate workpieces (E) |
0.81 |
0.04 |
21.66** |
0.66 |
The ability to plan a production (y16) |
0.84 |
< - > |
< - > |
0.72 |
The ability to follow procedures to create a workpiece (y17) |
0.81 |
0.03 |
24.94** |
0.67 |
The ability to summarize the production results (y18) |
0.86 |
0.04 |
21.76** |
0.74 |
The ability to present the produced workpiece (y19) |
0.75 |
0.04 |
20.65** |
0.57 |
The ability to analytically identify causes (F) |
0.92 |
0.04 |
25.27** |
0.85 |
The ability to identify causes of mistakes of the produced workpiece (y20) |
0.83 |
< - > |
< - > |
0.69 |
The ability to remediate the mistakes of the produced workpiece (y21) |
0.90 |
0.03 |
31.67** |
0.81 |
The ability to extensively develop the remedy for the mistakes of the produced workpiece (y22) |
0.89 |
0.03 |
31.09** |
0.79 |
The ability to work in collaboration (G) |
0.77 |
0.04 |
17.76** |
0.60 |
The ability to communicate during a collaboration (y23) |
0.74 |
< - > |
< - > |
0.54 |
The ability to cooperate during a collaboration (y24) |
0.73 |
0.03 |
24.53** |
0.53 |
The ability to exchange knowledge during a collaboration (y25) |
0.87 |
0.04 |
20.26** |
0.76 |
Chi-Square = 148.95, df = 149, P = 0.49, c2 /df = 0.999, RMSEA = 0.00, RMR = 0.0194, GFI = 0.985, AGFI = 0.967, PGFI = 0.452, CFI = 1.00 |
||||
Note: *p<.01, bsc refers to the standard factor loadings, therefore, the required
parameters indicated by the symbol, < - ->, do not report the S.E and t values
The results from the first-order confirmatory factor analysis revealed that all the primary computational thinking components demonstrated positive sub-component factor loadings ranging between 0.75-0.95 at a statistical significance at level 0.05. Ranked from high to low factor loadings, the component in priority order was the ability to use the information to solve problems (B); the ability to create workpieces (D); the ability to analytically identify causes (F); the ability to design countermeasures (C); the ability to analyze and manage data (A); the ability to evaluate workpieces (E); and the ability to work in collaboration (G) respectively with 0.95, 0.95, 0.92, 0.91, 0.83, 0.81, and 0.77 factor loadings. The measurement of all components (R2) also indicated a positive reliability as the variability of all sub-components in the seven components ranged between 0.68 and 0.90 which is as exhibited in Table 3-4 for the second-order confirmatory factor analysis using the Goodness of Fit Statistics
Respectively in priority, the second-order confirmatory factor analysis of computational thinking among preservice students in Thailand revealed seven primary components: the ability to use the information to solve problems (B); the ability to create workpieces (D); the ability to analytically identify causes (F); the ability to design countermeasures (C); the ability to analyze and manage data (A); the ability to evaluate workpieces (E); and the ability to work in collaboration (G) with a range of component reliability values from 0.75-0.95. The findings are consistent with Zhong et al. (2016), Swaid (2015), Lye & Koh (2014), Brennan & Resnick (2012), Basogain et al. (2017), and Gonzalez et al. (2017) which classify computational thinking in seven components, i.e., the ability to analyze and manage data (A); the ability to use the information to solve problems (B); the ability to design countermeasures (C); the ability to create workpieces (D); the ability to evaluate workpieces (E); the ability to analytically identify causes (F); and the ability to work in collaboration (G). Based on the findings, preservice teachers in Computer Education in Thailand prioritize d“the ability to use the information to solve problems” and “the ability to create workpieces” as they were the two with the highest factor loadings. The discovery is consistent with García-Peñalvo & Mendes (2017,) which states that many countries valued the importance of ICT competency development, especially in computational thinking, and the developments have been implemented in Primary to Tertiary Education to ensure that these citizens can live through technological challenges in their daily lives. Paula et al. (2018) discovers that one of the aims of the 21st-century education should be about the development of computational thinking as the skill deals with problem-solving which is especially valuable when interacting with digital technologies and different knowledge disciplines, e.g., Arts and Humanities. After reviewing the metadata of academic journals published during 2006- 2017, ChiaHsuShao et al. (2018) states that computational thinking has been heavily fostered with a rapid progression in the past-decade of education. The skill is vital for future lifestyles, especially among teachers and scholars, as most learning will occur through problem-solving situations. Similarly, Lye & Koh (2014) asserts that computational thinking is something more than coding when it comes to programming because it gives students the ability to solve problems through qualitative analysis using surrounding data. It is also a type of learning that emphasizes problem-solving through data processing to ensure a smooth workpiece production. Furthermore, Kazimoglu et al. (2012, p. 41) encourages the development of computational thinking through problem-solving in basic computer programming to create basic computer workpieces. YeonLee et al. (2014) and Shute (2017) mutually agree that building educational skills pertaining to computational thinking using effective problem-solving mindsets can help students invent suitable algorithms to help create the workpieces of their interests.
In conclusion, there are many types of thinking skills that can maximize the skills and knowledge of the 21st-century preservice teachers in Computer Education at Rajabhat universities in Thailand and help them construct high-performance technological and teaching innovations. In the future, these preservice teachers will become teachers in Computer and Technology. Hence, they should be knowledgeable about innovation and technology (Radicelli et al.; 2018); be able to innovate teaching technologies; know the knowledge transfer strategies that effectively expose students to computational thinking; and be able to foster systematic production of technological and innovative workpieces through proper work processes and sequences. Congruently, Titova et al. (2018) and Manson & Olsen (2010) employ popular teaching management strategies that integrate innovative teaching media with workpiece production. Currently, in Thailand, computational thinking is widely popular because nationwide basic curriculums have been revised to conform with the learning standards and indicators (Science Learning Strand Revised Edition, 2017) required by the Basic Education Core Curriculum B.E. 2561 (Ministry of Education, 2018). Specifically, the contents of the Computational Science Curriculum are consistent with Daily et al. (2015). Computational thinking is a beneficial future skill that helps students in Computer Education integrate technology-enhanced learning practices with computer innovations through computational-thinking sequences and processes.
Angeli, Charoula., Voogt, Joke., Fluck, Andrew., Webb, Mary., Cox Margaret., Malyn-Smith, Joyce., & Zagami, Jason. (2016). A K-6 Computational Thinking Curriculum Framework: Implications for Teacher Knowledge, 19. 47-57.
Aroian, K. J., & Norris, A.E. (2001). Confirmatory factor analysis. In B.H. Munro. Statistical methods for health care research. (4 th.ed.). Philadelphia: Lippincott William & Wilkins.
B. Daily, S., E. Leonard, A., Jörg, S., Babu, S., Gundersen, K., & Parmar, D. (2014). Embodying Computational Thinking: Initial Design of an Emerging Technological Learning Tool. Technology, Knowledge and Learning, 20(1), 79–84. doi:10.1007/s10758-014-9237-1.
Barr, Valerie., & Stephenson, Chris. (2011). Bringing computational thinking to K-12: what is Involved and what is the role of the computer science education community?. ACM Inroads, 2(1), 48-54. doi: 2. 10.1145/1929887.1929905.
Basogain, Xabier., Ángel Olabe Miguel., Carlos Olabe Juan., & Rico Mauricio. (2017). Computational Thinking in pre-university Blended Learning classrooms. Computers in Human Behavior, 80, p.412-419. doi: 10.1016/j.chb.2017.04.058.
Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. Presented at the American Education Researcher Association, Vancouver, Canada.
Bollen, K.A. (1989) Structural Equations with Latent Variables. John Wiley and Sons, Inc., New York. https://doi.org/10.1002/9781118619179.
Cuny, J., Snyder, L., & Wing, J.M. (2010). Demystifying computational thinking for noncomputer scientists. Unpublished manuscript in progress, referenced in http://www.cs.cmu.edu/~
CompThink/resources/TheLinkWing.pdf.
Shute, V. J., & Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking, Educational Research, 22, https://doi.org/10.1016/j.edurev.2017.09.003
Curran, P. J., West, S. G., & Finch, J. F. (1996). The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychological methods, 1(1), 16.
García-Peñalvo, Francisco., & Mendes, Antonio. (2017). Exploring the computational thinking effects in pre-university education. Computers in Human Behavior, 80, 407-411.
Román-González, Marcos., Pérez-González, Juan-Carlos., & Jiménez-Fernández, Carmen. (2017). Which cognitive abilities underlie computational thinking? Criterion validity of the Computational Thinking Test. Computers in Human Behavior, 72, 678–691.
González-Pereira, Borja., Vicente, Guerrero-Bote., & Moya-Anegon, Felix. (2010). A new approach to the metric of journals’ Scientific Prestige: the SJR indicator. Journal of Informetrics, 4(3), 379-391.
Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2010). Multivariate data analysis: A global perspective. Upper Saddle River, NJ: Pearson.
History of Rajabhat University. (2019). Establishment Milestones of Rajabhat. Retrieved from https://www.npru.ac.th/info/npru_profile.php .
Hsu, Ting., Chang, Shao-Chen., & Hung, Yu-Ting. (2018). How to learn and how to teach computational thinking: Suggestions based on a review of the literature. Computers & Education. doi:126. 10.1016/j.compedu.2018.07.004.
IFTF. (2011). Future Work Skills. Institute for the Future for University of Phoenix Research Institute. California, http://cdn.theatlantic.com/static/front/docs/sponsored/phoenix/future_work_ skills _2020.pdf.
Schnabel, Deborah. (2015). Future Work Skills. Welche Fertigkeiten verlangt die Arbeit der Zukunft?. 10.13140/RG.2.1.3839.4721.
Kazimoglu, Cagin., Kiernan, Mary., Bacon, Liz., & Mackinnon, Lachlan. (2012). A Serious Game for Developing Computational Thinking and Learning Introductory Computer Programming. Procedia - Social and Behavioral Sciences, 47, doi:1991-1999. 10.1016/j.sbspro.2012.06.938.
David A, Kenny., & D. Betsy, McCoach. (2003). Effect of the Number of Variables on Measures of Fit in Structural Equation Modeling, Structural Equation Modeling: A Multidisciplinary Journal, 10(3), 333-351. doi: 10.1207/S15328007SEM1003_1.
Lye, S. Y., & Koh, J. H. L. (2014). Review on teaching and learning of computational thinking through programming: What is next for K-12? Computers in Human Behavior, 41, 51-61. https://doi.org/10.1016/j.chb.2014.09.012.
Katrina, Falkner., Rebecca, Vivian. (2015). A review of Computer Science resources for learning and teaching with K-12 computing curricula: an Australian case study. Computer Science Education, 25(4), 390-429, doi: 10.1080/08993408.2016.1140410.
Manson, J., & Olsen, R. (2010). Assessing and refining an undergraduate computational science curriculum. Computer Science, 1(1), 857-865. https://doi.org/10.1016/j.procs.2010.04.094.
Marsh, Herb., Hau, Kit-Tai., R. Balla, John., & Grayson, David. (1998). Is More Ever Too Much? The Number of Indicators per Factor in Confirmatory Factor Analysis. Multivariate Behavioral Research - Multivariate Behavioral Research, 33, 181-220. doi:10.1207/s15327906mbr3302_1.
Matheus, L. (2017). Natural computing: concepts and applications of computing inspired by nature. Revista ESPACIOS, 38, 31.
Mejang, S. (2014). Advanced Statistics for Research: Theory and Practice (1st ed.). Bangkok: Chulalongkorn University Press.
Ministry of Education. (2016). The Twelfth Educational Development Plan of the Ministry of Education (2017-2021). Bangkok: Office of the Permanent Secretary to the Ministry of Education.
Ministry of Education. (2017). Learning Standards and Indicators for Mathematics and Science Learning Strands and Geography in Social Studies, Religions, and Cultures Learning Strands (Revision B.E. 2560) Under the Basic Education Core Curriculum B.E. 2551. Retrieved August 31, 2017 from http://opec.go.th/ckfinder/userfiles/files/general/123(2).pdf.
Mueller. (1996). Basic Principles of Structural Equation Modeling. New York, Springer-Verlag New York.Inc
Namthip, S., & Khongmalai, O. (2015). The Impact of Service Innovation to Competitive Advantage in Higher Education. SDU Research Journal, 11(2), 43-60.
Nimtrakul, B. (2016). The Development of Students' Relational Thinking in Mathematics Problem Solving Classroom. Journal of Education, 27(2), 70-81.
Office of the National Economic and Social Development Board. (2015). The Creation of the Twelfth National Economic and Social Development Plan (2017-2021). Retrieved March 27, 2015 from http://www.nesdb.go.th.
Partnership for 21st Century Learning. (2009). Framework for 21st Century Learning. Retrieved 19 May, 2015, from http://www.p21.org/our-work/p21-Framework.
Bruno, Paula., Andrew, Burn., Richard, Noss., & José, Valente. (2018). Playing Beowulf: Bridging computational thinking, arts and literature through game-making. International Journal of Child-Computer Interaction, 16, 39-46.
Perevoshchikova., BARBASHOVA., & ELIZAROVA . (2018). Final module certification project as a means of improving the quality of bachelor's training at the universities. Revista ESPACIOS, 39(38), 33.
Piatanom, S. (2008). Student Satisfaction Report on Services of Nakhon Pathom Rajabhat University. Retrieved from http://home.npru.ac.th/sommay/ebooks/book1.pdf
RADICELLI, García., POMBOZA, Floril., POMBOZA, Floril., FLORES, Franco., & CISNEROS, Barahona. (2018). Smart Education:Evaluación «ex ante» previo a la implementación de una estrategia de aprendizaje ubicuo en Smart Cities. Revista ESPACIOS, 39(15), 9.
Rafael, SANTOS., Sam, DEVINCENZI., Silvia, BOTELHO., & Marcos, BICHET. (2017). A model for implementation of educational cyber physical systems. Revista ESPACIOS, 39(10), 36.
Shute, J., Carriere, L., Duffy, D., Hoy, E., Peters, J., Shen, Y., & Kirschbaum, D. (2017). The Benefits and Complexities of Operating Geographic Information Systems (GIS) in a High Performance Computing (HPC) Environment. American Geophysical Union, Fall Meeting 2017.
Swaid. (2015). Bringing computational thinking to STEM educati.www.sciencedirect.com. Procedia Manufacturing, 3, 3657 – 3662. https://doi:10.1016/j.promfg.2015.07.761.
Teachers and Basic Education Personnel Development Bureau. (2010). Teacher Competency Assessment Tool (Revised Version), Bangkok: Office of the Basic Education Commission.
Elena, TITOVA., Evgenia, SAVOSTIANOVA., Vldimir YAKUSHEV., Pavel MATUCHIN., & Elena SAVCHENKO. (2018). Online Complex Supporting the Distance Education Course in HumanAnatomy for Foreign Pre-university Medical Students. Revista ESPACIOS, 39(10), 34.
Turchi., & Malizia. (2016). A Human-Centred Tangible approach to learning Computational Thinking. EAI Endorsed Transactions on Ambient Systems, 3(9), 6.
VIANA., Roberto., FRANCISCO., & SOARES. (2017). Computational simulation as a tool for analysis and scaling of the "Carro Rolão" feature in the beneficiation sector in a textile industry. Revista ESPACIOS, 39(6), 13.
UNESCO. (2008). UNESCO ICT competency framework for teacher. France: The United Nations Educational, Scientific and Cultural Oragnization.
Wing. (2006). Computational Thinking. COMMUNICATIONS OF THE ACM, 49(3).
Yasemin, Allsop. (2019). Assessing computational thinking process using a multiple evaluationapproach. International Journal of Child-Computer Interaction, 19, 30-55. https://doi.org/10.1016/j.ijcci.2018.10.004.
Yeon, Lee., Jeong, Hwi., Han, M., & Kim, Chan Hyeong. (2014). Tetrahedral-mesh-based computational human phantom for fast Monte Carlo dose calculations. Physics in Medicine and Biology, 59(12).
Zhong, et. al. (2016). Image-based computational quantification and visualization of genetic alterations and tumour heterogeneity. Scientific Reports. Article number: 24146 http://DOI: 10.1038/srep24146.
Zhong, Qing., Rüschoff, Jan., Guo, Tiannan., & Gabrani, Maria. (2016). Image-based computational quantification and visualization of genetic alterations and tumour heterogeneity. Scientific Reports, 6, doi:10.1038/srep24146.
Zhong, B., Wang, Q., Chen, J., & Li, Y. (2016). An exploration of three-dimensional integrated assessment for computational thinking. Journal of Educational Computing Research, 53(4), 562–590. http://dx.doi.org/10.1177/0735633115608444.
1. Phd Candidate of Computer Education, Department of Industrial Education, Faculty of Industrial and Technology Education King Mongkut's Institute of Technology Ladkrabang, Thailand. Email: aor030@gmail.com
2. Teacher,(Education). Assist.Prof.Dr. Sirirat Petsangsri. Department of Industrial Education, Faculty of Industrial and Technology Education King Mongkut's Institute of Technology Ladkrabang , Thailand. Email: kpsirira@kmitl.ac.th