

 Vol. 40 (Nº 26) Año 2019. Pág. 24
Vol. 40 (Nº 26) Año 2019. Pág. 24
TORRES P., Roberto C. 1 & FALK D., Mary 2
Recibido: 20/03/2019 • Aprobado: 27/07/2019 • Publicado 29/07/2019
RESUMEN: Este artículo presenta la construcción del concepto de probabilidad que elaboran estudiantes de primer semestre de ingeniería enfrentados a la resolución de problemas. Haciendo un análisis basado en la taxonomía SOLO (Structure of Observed Learning Outcome) y la resolución de problemas, se observa que los estudiantes razonan basados en sus creencias personales, abordan situaciones con estrategias de representación, razonan basados en hechos concretos resultado del ensayo, finalmente razonan a partir de la construcción del espacio muestral, demostrando crecimiento en la construcción del concepto de probabilidad. |
ABSTRACT: This article presents the construction of the concept of probability developed by first-semester engineering students facing problem solving. Making an analysis based on the SOLO (Structure of Observed Learning Outcome) taxonomy and problem solving, it is observed that the students reason based on their personal beliefs, approach situations with representation strategies, reason based on concrete facts resulting from the essay, finally reason from the construction of the sample space, demonstrating growth in the construction of the concept of probability. |
Es natural pensar que desde sus orígenes las civilizaciones se hayan visto obligadas a resolver problemas de conteo y probabilidad, así como también problemas relacionados con la organización y sistematización de la información. Según (Burton, 2011) “El recuento directo de la población y la riqueza económica se remonta a la antigüedad. La numeración del pueblo de Israel, los balances del Emperador Augusto sobre el Imperio Romano y el inventario de sus posesiones, el Libro del Juicio Final (llamado así por los ingleses porque no había apelación de él) son algunos de los más destacados ejemplos históricos de recolección de datos”.
Para (Daston, 1988) la teoría clásica de la probabilidad se desarrolló entre aproximadamente 1650 y 1840. Matemáticos del calibre de Blaise Pascal, Jakob Bernoulli y Pierre Simón Laplace trabajaron sobre un modelo de decisión racional, acción y creencia bajo condiciones de incertidumbre. Casi todos los problemas que se dirigieron se expresaron en estos términos: ¿Cuándo es racional comprar un boleto de lotería? ¿Aceptar una hipótesis científica? ¿Vender una expectativa de una herencia futura? ¿Creer en Dios? ¿Invertir en una anualidad?, en ese sentido, la teoría matemática de las probabilidades debía ser la codificación de una nueva marca de racionalidad, que contribuye con la toma de decisiones en situaciones de incertidumbre o azar.
Por otro lado, en reconocimiento de la importancia que tiene en una gran gama de profesiones y para que el ciudadano común pueda tomar decisiones personales y políticas, se ha incluido la probabilidad en los programas de estudio a partir de la escuela primaria en muchos países. Debido a ello, es importante reflexionar sobre las ideas principales que los estudiantes deben adquirir en diferentes edades, los rasgos del razonamiento probabilístico informal, métodos de enseñanza apropiados, situaciones de enseñanza adecuada y experiencias exitosas de enseñanza.
Para (Nunes, Brant, & Evan, 2015) uno de los aspectos relevantes del estudio de la probabilidad es la alfabetización estadística en la población en general. Tanto a los adultos como a los niños a menudo les resulta difícil pensar racionalmente acerca de la probabilidad y la aleatoriedad, por lo que los encuentros tempranos con estos conceptos dan inicio a la posibilidad de analizar y dominarlos.
El pensamiento probabilístico o estocástico ayuda a tomar decisiones en situaciones de incertidumbre, de azar, de riesgo por falta de información confiable, en las que no es posible predecir con seguridad lo que va a pasar. Se apoya directamente en conceptos y procedimientos de la teoría de probabilidades y de la estadística inferencial, e indirectamente en la estadística descriptiva y en la combinatoria. Ayuda a buscar soluciones razonables a problemas en los que no hay una solución clara y segura, abordándolos con un espíritu de exploración y de investigación mediante la construcción de modelos de fenómenos físicos, sociales o de juegos de azar y la utilización de estrategias como la exploración de sistemas de datos, la simulación de experimentos y la realización de conteos.
Por otro lado, según (Mooney, Langrall, & Hertel, 2014) se han identificado los marcos de investigación del pensamiento probabilístico, encontrando dos grupos de investigación responsables del desarrollo de estos marcos, uno en los Estados Unidos dirigido por Graham Jones y otro en Australia, dirigido por Jane Watson. Una característica de estos marcos es que todos usan la conocida taxonomía SOLO (Structure of Observed Learning Outcome) como base para caracterizar el pensamiento de los estudiantes.
Los autores manifiestan que se ha caracterizado el pensamiento en los niveles distinguidos en esa taxonomía como preestructural, uniestructural, multiestructural y relacional pero los investigadores no han caracterizado el pensamiento en lo que se ha denominado el nivel abstracto extendido. Hasta donde es sabido, el desarrollo de este nivel de sofisticación del pensamiento probabilístico todavía no se ha caracterizado en un marco organizado. El propósito de la investigación sobre la cual el presente artículo está informando es comenzar a avanzar hacia una tal caracterización.
Por otra parte (Ben-Zvi & Garfield, 2005) afirman que “la información cuantitativa está en todas partes, y las estadísticas se presentan cada vez más como una manera de agregar credibilidad a anuncios, argumentos, o consejos, además, ser capaz de evaluar adecuadamente las pruebas (datos) y las reclamaciones basadas en datos es una habilidad importante que todos los estudiantes deben aprender como parte de sus programas educativos”. Sin embargo, es común encontrar en los estudiantes de ingeniería notables deficiencias en cuanto al desarrollo del pensamiento probabilístico y la resolución de problemas con contenidos de probabilidad, ya que centran su estudio en el desarrollo de contenidos y dedican poco a la solución de problemas retadores o históricos que son importantes para el desarrollo del pensamiento y la construcción del significado del concepto de probabilidad.
Es importante resaltar que, actualmente el proceso de enseñanza aprendizaje de la matemática es de especial interés para la comunidad científica particularmente para los educadores e investigadores en educación matemática. De la misma manera lo es también el proceso de enseñanza aprendizaje de la estadística y en especial de la probabilidad y el desarrollo del pensamiento probabilístico. En ese sentido (Sánchez & Landín, 2014) a partir de los niveles de complejidad de la taxonomía SOLO describen algunos aspectos del proceso por el cual los estudiantes llegan a conocer y utilizar la fórmula de probabilidad binomial. El trabajo se realizó en el contexto de un curso común de probabilidad y estadísticas de la escuela secundaria de México. Específicamente el trabajo se desarrolló con 66 estudiantes de la escuela secundaria (17-18 años) después de participar en un curso de probabilidad. Para el desarrollo de la investigación los autores diseñaron una prueba de ocho problemas para explorar el desempeño de los estudiantes en situaciones de probabilidad binomial, para lo cual diseñaron una jerarquía de razonamiento basada en la taxonomía SOLO, para clasificar las respuestas de los estudiantes en diferentes niveles de razonamiento. Para describir el proceso por el cual los estudiantes llegan a conocer y utilizar la fórmula de probabilidad binomial los autores definieron cinco niveles de razonamiento. Nivel 1. Las respuestas son idiosincrásicas o influenciadas por el sesgo cognitivo, como representatividad, la ilusión de linealidad, el supuesto incorrecto de equiprobabilidad u otras razones. Nivel 2. Las respuestas se basan en una descripción del espacio muestral, posiblemente incompleta, y en el uso de la definición de probabilidad clásica. La regla del producto puede ser utilizada, pero con errores u operaciones parciales. Nivel 3. Las respuestas correctas se caracterizan por el uso de procedimientos combinatorios y la definición clásica de probabilidad, generalmente apoyada por diagramas de árbol. Nivel 4. Las respuestas correctas se caracterizan por el uso de regla de producto y procedimientos combinatorios, en su mayoría acompañados de diagramas de árbol. La fórmula de las combinaciones se utiliza para calcular coeficientes binomiales. Nivel 5. El uso correcto de la fórmula binomial se muestra en este nivel. Los valores de los parámetros son identificados.
Por otra parte (Retamal, Alvarado, & Rebolledo, 2007) Intenta dar respuesta parcial a los interrogantes. ¿Es posible introducir la simulación en conceptos de distribuciones muestrales debido a la gran complejidad de su aparato analítico? ¿Los estudiantes aplican correctamente los diversos elementos de significados de propiedades en la resolución de problemas? ¿Los estudiantes adquieren destrezas en planear un diseño muestral? El autor considera diferentes entidades primarias que constituyen el significado de un objeto matemático (en este caso, las distribuciones muestrales). Problemas y situaciones que inducen actividades matemáticas y definen el problema asociado al objeto. Procedimientos y operaciones algorítmicas. Representaciones materiales utilizadas en la resolución de problemas. Abstracciones. Demostraciones. Según el autor, los estudiantes presentan dificultades al momento de aplicar las propiedades de las distribuciones muestrales, la mayoría de los estudiantes escriben correctamente los términos, variables y símbolos y se apropian de las notaciones empleadas, aplican correctamente el procedimiento del cálculo de distribuciones muestrales, pero muchos presentan dificultades al llegar a la solución correcta de probabilidad usando la media de distribución muestral, carecen de síntesis de conceptos y solo pueden reproducir definiciones aisladas, reconocen y se apropian en su mayoría de las propiedades y son incorporados a sus conocimientos, en general los estudiantes utilizan bien el algoritmo, las propiedades, definiciones y procedimientos algebraicos, pero no interpretan ni hacen síntesis de los resultados.
Por su parte (Way, 2003) en una investigación realizada con 74 niños de cuatro a doce años, que no habían recibido ninguna instrucción formal previa en cuanto a contenidos de probabilidad analiza las tareas realizadas, confirmando la presencia de tres etapas de desarrollo del pensamiento probabilístico en los niños, pero también reveló dos etapas transitorias distintas. Según (Way, 2003) el trabajo se centró en las características de las estrategias de los niños para hacer juicios probabilísticos en cada etapa, y cuáles son las implicaciones de tales juicios en el proceso de enseñanza. Según la autora, los niños alrededor de la edad de nueve años habían construido algunos de los conceptos que proporcionan una base para la probabilidad y demuestran el aprendizaje en la participación de las tareas de razonamiento de probabilidad. A esta edad, es probable que los estudiantes se beneficien de la instrucción que les permite hacer conexiones entre conceptos (tanto dentro del tema de la probabilidad como a través de ideas matemáticas que se alinean con la probabilidad) y expandir sus estrategias numéricas tempranas en un pensamiento proporcional más sofisticado.
La población la integran estudiantes de primer semestre de la facultad de ingeniería de la Universidad del Magdalena matriculados en el curso Estadística I. Este estudio se desarrolla bajo un paradigma cualitativo, donde se muestran los fundamentos teóricos asociados con el desarrollo del pensamiento probabilístico y el proceso de resolución de problemas. En el desarrollo de la investigación se utilizaron métodos teóricos y empíricos (observación participante, actividades de resolución de problemas y una encuesta).
Durante la investigación se utilizan juegos didácticos que favorecen el desarrollo del pensamiento probabilístico, guías o actividades con situaciones o problemas con contenidos de probabilidad, tomados del contexto histórico, cotidiano y de la ingeniería, entre otros. Las actividades de resolución de problemas, están orientadas a contribuir con la construcción del significado de los conceptos y constatar cómo se desarrolla el pensamiento en el proceso de resolución de problemas con contenidos de probabilidad.
El proceso en el aula estaba caracterizado por tres fases. En la fase introductoria, se plantean problemas del contexto histórico, paradojas y problemas retadores que el estudiante deberá resolver sin la introducción de conceptos previos, haciendo uso únicamente de lo que él dispone en su formación. Luego sigue la fase de desarrollo, que consiste en la construcción del significado de los conceptos por parte de los estudiantes bajo la orientación del profesor, donde se hace la introducción o presentación gradual de conceptos a través de la estrategia didáctica elegida para tal fin. Sigue la fase final donde se plantean nuevos problemas con mayor nivel de complejidad o dificultad elegidos del contexto histórico, del contexto de la carrera y de las matemáticas mismas, que conducirán a los estudiantes a la construcción robusta del significado de los conceptos de probabilidad.
El proceso de construcción del significado de los conceptos de probabilidad se llevó a cabo a partir del planteamiento de preguntas y respuestas a interrogantes ligados a los problemas planteados de modo que el estudiante va construyendo paso a paso el concepto de probabilidad y adquiere habilidades para la solución de nuevos problemas, cada vez más retadores. Preguntas como: ¿Qué pasaría si…?, ¿y ahora si en vez de … hace…?, la introducción de los conceptos se desarrolló a través de notas históricas a manera de ¿sabías que …?
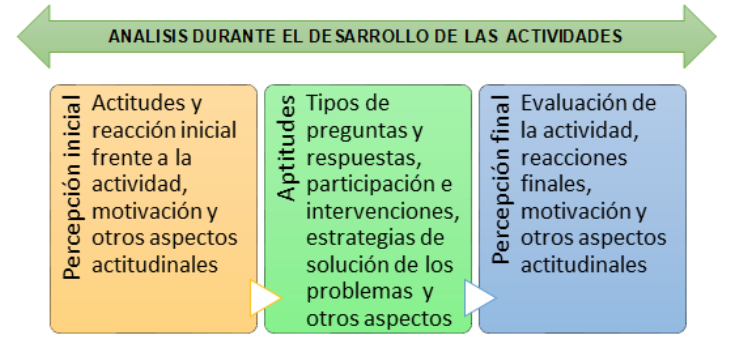
Para el proceso de análisis se tuvo en cuenta dos momentos. El primer momento será durante el desarrollo de las actividades; en ese momento se hará un análisis de la percepción inicial de los estudiantes frente al desarrollo de la actividad, es decir, actitudes y reacción inicial frente a la actividad, motivación y otros aspectos actitudinales, también se hará un análisis de las aptitudes, es decir, tipos de preguntas y respuestas, participación e intervenciones, estrategias de solución de los problemas y otros aspectos derivados de los criterios definidos a priori en la taxonomía SOLO. Por último, se analizará la percepción final de los estudiantes, que consiste en la evaluación de la actividad, reacciones iniciales, motivación y otros aspectos actitudinales.
Ilustración 1
Proceso de análisis de las actividades en clases
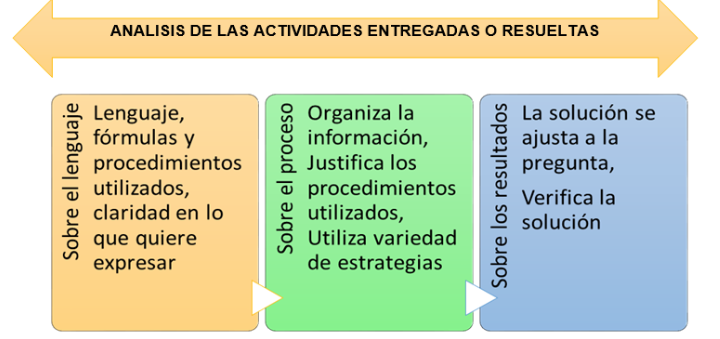
El segundo momento es el análisis de las actividades entregadas o resueltas; en este momento se hace una revisión y análisis del lenguaje utilizado para comunicar las ideas, que consiste en el lenguaje, fórmulas y procedimientos utilizados y la claridad en lo que quiere expresar. Además, se analiza el proceso de resolución de los problemas planteados, teniendo en cuenta si el estudiante organiza la información, justifica los procedimientos utilizados, utiliza variedad de estrategias, y demás aspectos propios de la resolución de problemas. Finalmente se hace un análisis sobre los resultados obtenidos, es decir, si la solución se ajusta a la pregunta, verifica la solución etc.
Ilustración 2
Proceso de análisis de las actividades entregadas o resueltas
Para el análisis de las actividades se tuvo en cuenta los siguientes elementos.
Ilustración 3
Tipos de problemas planteados
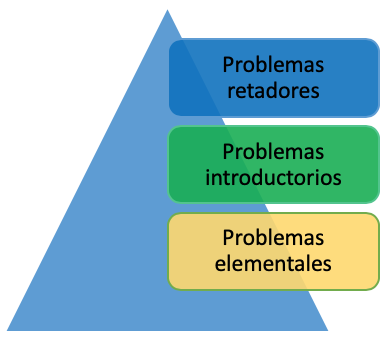
Son las situaciones que eventualmente no requieren de mayor crecimiento en cuanto al desarrollo de herramientas conceptuales para su solución, pero que resultan ser motivadores y de agrado para los estudiantes.
Con un nivel de complejidad mayor al de los problemas elementales, éstos abordan situaciones a las que se enfrenta un estudiante o un grupo de estudiantes, para las cuales el camino o medio para su solución no es evidente y se requiere poner a prueba la creatividad y el trabajo en equipo para construir una avenida de acceso y los medios para transitar por ella.
Con un grado de complejidad mayor, los problemas retadores abordan situaciones motivadoras que se constituyen en un desafío para los estudiantes y en las que se conjugan la creatividad, la autonomía, la crítica reflexiva, la indagación, el trabajo en equipo y el razonamiento para la consecución de soluciones acertadas y verificables.
Basado en el enfoque de solución de problemas y la heurística definida por (Polya, 1981) para dicho proceso, se observarán en los estudiantes tres niveles de desarrollo en el proceso de resolución de problemas de probabilidad, nivel inferior, nivel medio y nivel alto, como se muestra en la siguiente tabla.
Tabla 1
Evidencias en el proceso de resolución
de problemas de probabilidad
Acciones |
Nivel inferior |
Nivel medio |
Nivel alto |
Búsqueda de una posible solución |
No organiza la información |
Organiza la información |
Organiza la información |
Verificación de la solución encontrada |
No verifica la solución encontrada |
Verifica la solución en los casos que los procedimientos son generales o estándar |
Dispone de varias estrategias para verificar la solución |
Planteamiento de nuevas preguntas o problemas |
No puede obtener el resultado en forma diferente, no deriva preguntas nuevas a partir del problema o de su solución |
Deriva nuevas preguntas a partir del problema cuya respuesta es evidente |
Deriva nuevas preguntas del problema o su solución que se constituyen en un nuevo reto |
Fuente: Adaptado por el autor de (Rodríguez, 2001)
Es importante resaltar que el propósito de este trabajo no es clasificar a los estudiantes según el nivel de desarrollo del pensamiento, se trata de presentar los elementos o características que evidencian los estudiantes en el proceso de solución de problemas con contenidos de probabilidad. La tabla anterior contiene algunos criterios a priori, que luego de ser observados, permitirán explicar algunos elementos involucrados en el proceso de resolución de problemas de los estudiantes en las diferentes etapas y así ponderar si hubo avances, o por el contrario la metodología utilizada es cuestionada o modificada.
Teniendo en cuenta que los estudios realizados sobre pensamiento probabilístico, proporcionan una descripción del crecimiento del pensamiento probabilístico de los estudiantes, en los niveles preestructural, uniestructural, multiestructural y relacional, de acuerdo con la Taxonomía SOLO, estos marcos se han desarrollado a través del trabajo en las aulas y con los estudiantes. Según (Mooney, Langrall, & Hertel, 2014) los investigadores han considerado las implicaciones del proceso de enseñanza en su trabajo. Por lo que, estos marcos proporcionan un puente entre la teoría del aprendizaje y las prácticas de enseñanza, pero no hacen una caracterización del pensamiento probabilístico con estudiantes en el estadio de las operaciones formales.
La taxonomía (SOLO) de (Biggs & Collis, 1982) será utilizada para ayudar a definir criterios a priori que permitan explicar el pensamiento probabilístico manifestado por los estudiantes en el proceso de resolución de problemas, pero a la vez se analiza la posibilidad de evaluar la aplicabilidad de esta metodología en la caracterización del pensamiento matemático en general y en particular del pensamiento probabilístico.
A partir de los resultados de las investigaciones analizadas y los planteamientos de la Taxonomía SOLO se establecen los criterios a priori que posibilitarán presentar avances en la caracterización del pensamiento manifestado por los estudiantes de ingeniería de la Universidad del Magdalena en el proceso de resolución de problemas con contenidos de probabilidad.
Tabla 2
Criterios a priori para el análisis del pensamiento probabilístico.
Nivel Pre estructural |
Nivel Uniestructural |
Nivel Multi estructural |
Nivel relacional |
Nivel abstracto extendido |
Tener una comprensión intuitiva de la aleatoriedad. |
Tendencia a volver al pensamiento probabilístico subjetivo. |
Hacer uso de razones, cuentas, probabilidades o probabilidades para juzgar situaciones probabilísticas. Crear sistemáticamente espacios de muestras para los experimentos. Proporcionar ejemplos de situaciones aleatorias. Reconocer los cambios en la probabilidad y la independencia en los eventos sin reemplazo. Hacer predicciones que a veces dependen de estrategias de representatividad. |
Razonar con probabilidades Examinar la distribución de los resultados sin volver a las estrategias de representatividad. |
Generalizar. Las respuestas van más allá de la descripción llegando a la explicación |
Fuente: Adaptado por el autor de (Biggs & Collis, 1982)
A partir del planteamiento de situaciones elementales sin la introducción de conceptos, se observó que los estudiantes en su mayoría comprenden los conceptos y vocabulario asociado con el azar, la incertidumbre y la probabilidad, relacionan el valor de la probabilidad de un suceso con el número de veces que éste ocurre, distinguen fenómenos aleatorios de los deterministas, comprenden la probabilidad de eventos en el contexto cotidiano, reconocen situaciones igualmente probables, y hacen inferencias a partir de los resultados del ensayo.
Ilustración 4
Solución actividad 1 estado inicial

-----
Ilustración 5
Solución actividad 1, estado inicial

En la pregunta 1 el estudiante establece las relaciones en el diagrama, distingue fenómenos aleatorios y palabras relacionadas con el azar, en la pregunta 2 compara y cuantifica probabilidades, y en la pregunta 5 usa diagramas de árbol para considerar todos los casos posibles, es decir, usa estrategias de representación para considerar todos los casos posibles y favorables
Otro elemento que se pudo observar en algunos estudiantes es el razonamiento basado en sus creencias para estimar el valor de la probabilidad de un evento sin hacer un análisis profundo de la situación; no se considera el espacio muestral por lo tanto el estudiante no considera los casos posibles y favorables a un suceso.
Luego de una introducción o presentación gradual de conceptos a través del planteamiento y solución de problemas, elementales, introductorios y retadores, además del planteamiento constante de preguntas y respuestas a interrogantes ligados a los problemas planteados. Se observó el avance de algunos estudiantes en la construcción de significado del concepto de probabilidad a través del proceso de planteamiento y resolución de problemas, encontrando que parte de ellos presentan argumentos basados en la descripción del espacio muestral, dominan el cálculo elemental de probabilidades, agrupan todos los resultados posibles y favorables de un evento, relacionan la probabilidad de un suceso con la razón entre el número de casos favorables y el número de casos posibles, elaboran esquemas, gráficas, tablas, etc. que representan el problema o parte del problema y que contribuyen a su comprensión, hacen predicciones que dependen de estrategias de representación, elaboran modelos o esquemas que les permiten analizar el problema y explicar su solución, relacionan la probabilidad teórica con la frecuencia relativa, reconocen eventos complementarios, relacionan la probabilidad de un suceso con el espacio muestral, reconocen eventos seguros, imposibles, mutuamente excluyentes y complementarios, reconocen eventos dependientes e independientes y reconocen cambios en el valor de la probabilidad con y sin reemplazo.
Otro aspecto que se pudo observar en los estudiantes es que pocas veces incorporan el lenguaje formal a sus argumentos y en ocasiones presentan razonamientos basados en su experiencia o conocimiento acumulado.
Ilustración 6
Razonamientos de los estudiantes basados en la experiencia o conocimiento acumulado

Note que en la pregunta 5, los estudiantes responden, al lanzar una moneda 4 veces se tendrán 8 posibilidades, que salgan 2 caras es 2 de 8 y al menos 2 caras es 2 de 8 también
Finalmente se observó en los estudiantes avances significativos en la construcción de significado del concepto de probabilidad lo que se pudo evidenciar en la adición de nuevas manifestaciones del pensamiento a sus estructuras iniciales. Entre las características del pensamiento observadas en los estudiantes se encuentran las siguientes. Analizan todos los resultados o casos posibles y favorables de una situación antes de hacer el cálculo de la probabilidad, relacionan la probabilidad de un suceso con la razón entre el número de casos favorables y el número de casos posibles para estimar el valor de la probabilidad, comparan y cuantifican los valores de las probabilidades para hacer conclusiones, formulan estrategias adecuadas para resolver problemas de probabilidad que involucran elaboración del espacio muestral utilizando estrategias de representación, emplean correctamente la regla de Laplace y la probabilidad de eventos complementarios, reconocen eventos dependientes e independientes y usan éstos para estimar los cambios en el valor de la probabilidad con y sin reemplazo.
Ilustración 7
Avances en los razonamientos de los estudiantes

En las respuestas planteadas por el estudiante en la situación 1 demuestra crecimiento en su construcción del concepto de probabilidad frecuentista ya que para sus argumentos tiene en cuenta el número de ensayos para una mejor estimación del valor de la probabilidad. Por otra parte, en la situación 4 el estudiante razona basado en la construcción del espacio muestral y luego calcula el valor de las probabilidades.
También se observaron mínimos avances en ciertos estudiantes que no adicionaron nuevas manifestaciones del pensamiento a sus estructuras iniciales, predominando el razonamiento basado en las creencias o conocimiento acumulado por la experiencia. Por ejemplo, estos estudiantes no llegan a consideran la influencia del número de ensayos para estimar la probabilidad de un suceso en el enfoque frecuentista.
Ilustración 8
Muestra de avances mínimos en la construcción de conceptos

En las respuestas planteadas por el estudiante en la situación 1 se evidencia poca claridad en el concepto frecuentista de la probabilidad al considerar aceptable el experimento de la persona 1 con sólo dos lanzamientos de la moneda; el estudiante considera correctos los planteamientos teniendo en cuenta que en los valores de las probabilidades complementarias, la suma de los numeradores coincidan con el número de lanzamientos, sin tener en cuenta la cantidad de lanzamientos para considerar aceptable o no el experimento de cada persona.
Es importante resaltar que el análisis de las actividades se realizó teniendo en cuenta los criterios preestablecidos en la taxonomía SOLO y aquellos que surgieron y que no se habían tenido en cuenta previamente. Además, se valoraron los avances del estudiante en cuanto a la comprensión y apropiación de los conceptos y la resolución de problemas.
El planteamiento de problemas con contenidos de probabilidad en el contexto histórico, cotidiano y de la ingeniería posibilita el desarrollo del pensamiento probabilístico toda vez que se tenga conciencia de las conexiones existentes entre los conceptos probabilísticos con otros conceptos matemáticos. Por ejemplo, la claridad que se debe tener acerca de la relación entre la medida de la probabilidad clásica presentada por Laplace, donde se define la probabilidad de ocurrencia de un evento A como el cociente entre el número de casos favorables al evento y el número de casos posibles, con el concepto de razón como una comparación mediante el cociente y no como el resultado de la división, es fundamental para la comprensión del concepto de probabilidad, ya que permite expresar la probabilidad de un evento como “cuántos de tantos” y no como un número abstracto.
El establecimiento de tales conexiones contribuye a que los alumnos desarrollen hábitos que los lleven a buscar, reconocer y crear enlaces entre los conceptos matemáticos con otros conceptos y entre los conceptos matemáticos con las ciencias y la vida cotidiana.
Por otra parte, el planteamiento de preguntas bien seleccionadas, resultado de un proceso riguroso de análisis y evaluación, provee una herramienta excepcional para caracterizar el pensamiento matemático.
Ben-Zvi, D., & Garfield, J. (2005). Statistical Literacy, Reasoning, and Thinking Goals, Definitions, and Challenges. En D. Ben-Zvi, & J. Garfield, The Challenge of Developing Statistical Literacy, Reasoning and Thinking. Springer Science + Business Media, Inc.
Biggs, J., & Collis, K. (1982). Evaluating The Quality Of Learning, The SOLO taxonomy (Structure of the Observed Learning Outcome). . ACADEMIC PRESS.
Burton, D. (2011). The History of Mathematics an Introduction. McGraw-Hill.
Daston, L. (1988). Classical Probability in the Enlightenment. . Princeton University press.
Mooney, E., Langrall, C., & Hertel, J. (2014). A practitional Perspective on Probabilistic Thinking Models and Frameworks. En B. S. Egan J. Chernoff, Proababilistiic Thinking (págs. 495-499). Springer.
Nunes, T., Brant, P., & Evan, D. (2015). Teaching Probability in Primary School. Oxford.
Polya, G. (1981). Mathematical Discovery. On understanding, learning and teaching problem solving. Combined Edition. New York: Wiley & Sons, Inc.
Retamal, L., Alvarado, H., & Rebolledo, R. (2007). Comprensión de las distribuciones muestrales en un curso de estadística para ingenieros. Revista Chilena de ingeniería.
Rodríguez, M. A. (2001). Resolución de Problemas. En M. D. Pochulu, & M. A. Rodríguez, EDUCACIÓN MATEMÁTICA, APORTES A LA FORMACIÓN DOCENTE DESDE DISTINTOS ENFOQUES TEÓRICOS (pág. 158).
Sánchez , E., & Landín, P. R. (2014). Levels of Probabilistic Reasoning of High School Students About Binomial Problems findings. En E. Chernoff, & B. Sriraman, Probabilistic Thinking (págs. 580-596). Springer.
Way, J. (2003). The Development of Young Children’S Notions of Probability. CERME III Italy.
1. Docente de Matemáticas de la Facultad de Ingeniería de la Universidad del Magdalena, Santa Marta Colombia. Email- rocato39@gmail.com
2. Docente investigador y directora de los programas de Maestría y Doctorado en Educación Matemática de la Universidad Antonio Nariño, Bogotá Colombia. Email- maridelosada@gmail.com