

 Vol. 40 (Nº 2) Ano 2019. Pág. 24
Vol. 40 (Nº 2) Ano 2019. Pág. 24
HALLAL, Renato 1; PINHEIRO, Nilcéia A. M. 2; PANDIM, Fábio J. 3; PRADO, Naimara V. 4
Recebido: 15/08/2018 • Aprovado: 20/12/2018 • Publicado 21/01/2019
RESUMO: O objetivo deste artigo é apresentar a produção científica de estudos voltados a área do ensino, que utilizaram da metodologia Resolução de Problemas como uma alternativa no processo de ensino-aprendizagem de matemática. Para isso, utilizou-se a base de dados SciELO integrada a revista BOLEMA como fonte de pesquisa e seleção dos trabalhos publicados no período de 2012 a 2017. Os artigos selecionados foram analisados por meio de uma revisão. O descritor utilizado foi Resolução de Problemas. Durante a revisão, fez-se uma síntese geral dos trabalhos. Os resultados mostraram-se satisfatórios. |
ABSTRACT: The purpose of this article is to present the scientific production of studies focused on the teaching area, which used the Problem Solving methodology as an alternative in the teaching-learning process of mathematics. For this purpose, the SciELO database integrated to BOLEMA magazine was used as a research and selection source for papers published in the period from 2012 to 2017. The articles selected were analyzed by means of a review. The descriptor used was Troubleshooting. During the review, a general overview of the work was done. The results were satisfactory |
Um dos aspectos fundamentais que rege as mudanças educacionais e estimula as diferentes pesquisas em educação são o fato de se buscar desenvolver nos alunos a capacidade de aprender a aprender. Assim, o desafio no processo educativo, em termos introdutórios e instrumentais, é construir condições do aprender a aprender e do pensar (DEMO, 1996, p. 30).
Nas diferentes áreas da educação percebe-se a necessidade de que os alunos obtenham habilidades e estratégias que lhes proporcionem a assimilação, por si mesmos, de novos conhecimentos e não apenas a obtenção de conhecimentos prontos e acabados.
Visando uma sociedade mais justa, capaz de intervir no desenvolvimento da humanidade crítica e, criativamente, buscando uma melhoria na qualidade de vida do cidadão, não é suficiente apresentar conhecimentos cristalizados e fora do contexto moderno. É preciso fazer com que os alunos se tornem pessoas capazes de enfrentar situações diferentes dentro de contextos diversificados, que façam com que eles busquem aprender novos conhecimentos e habilidades, só assim, estarão melhor preparados para adaptar-se as mudanças culturais, tecnológicas e profissionais da atualidade (SOARES & PINTO, 2001).
A aula meramente expositiva está ultrapassada. O aluno não pode ser um repetidor de informações. O professor deve instigar o aluno a pensar, formar e expressar a sua própria opinião. Espera-se do professor uma nova postura, um professor capaz de ajustar suas didáticas as novas exigências da sociedade. Segundo Soares e Pinto (2001), os professores precisam compreender seu papel incentivador, facilitador e mediador das ideias apresentadas pelos alunos, de modo que, estas sejam produtivas, levando os alunos a refletirem e a gerarem seus próprios conhecimentos.
Portanto, a busca por diferentes metodologias de ensino que visam o engajamento dos estudantes durante todo o processo de aprendizagem se fazem necessárias, sendo uma destas, conhecida por metodologia de resolução de problemas. Mediante o exposto, o objetivo deste trabalho é fazer uma revisão da literatura acerca desta metodologia, utilizando como fonte de pesquisa a revista BOLEMA (Boletim de Educação Matemática), as quais estão fixadas na plataforma SciELO. Os autores deste trabalho, decidiram analisar a BOLEMA por ser considerada uma das mais antigas e importante revista na área de Educação Matemática no Brasil, avaliada pela CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior) com Qualis A1.
A resolução de problemas, como uma metodologia de ensino, se torna o lema de pesquisas e estudos nos anos de 1990 (ALLEVATO & ONUCHIC, 2008). Esta nova visão de ensino e aprendizagem de matemática, se apoia nos estudos desenvolvidos pelo NCTM (National Council of Teachers of Mathematics), que resultou na publicação dos Standards 2000, oficialmente chamado de, Princípios e Padrões para a Matemática Escolar (ONUCHIC & ALLEVATO, 2005; ONUCHIC & ALLEVATO, 2011). Esta publicação, destaca George Polya, como um dos impulsionadores da resolução de problemas. Apoiado as ideias dos Standards do NCTM, foram criadas os PCN - Parâmetros Curriculares Nacionais (BRASIL, 1997, 1998, 1999), que apontam o desenvolvimento da capacidade de resolver problemas, explorá-los, generalizá-los e até propor novos problemas a partir deles, como um dos propósitos do Ensino de Matemática; indicam a resolução de problemas como ponto de partida das atividades matemáticas e discutem caminhos para se fazer matemática na sala de aula.
Logo, um dos desafios do ensino da matemática é a abordagem de conteúdos para a resolução de problemas. Trata-se de uma metodologia pela qual o estudante tem oportunidade de aplicar conhecimentos matemáticos adquiridos em novas situações, de modo a resolver a questão proposta (DANTE, 2003; GOV, 2008).
Para Dante (2003), um problema é qualquer situação que exija a maneira matemática de pensar e conhecimentos específicos para solucioná-los, deste modo, um bom problema deve: (a) ser desafiador para o aluno, (b) ser real, (c) ser interessante, (d) ser o elemento de um problema desconhecido, (e) não consistir na aplicação evidente e direta de uma operação aritmética e, (f) ter um nível adequado de dificuldade. Onuchic (1999) define como problema tudo aquilo que não se sabe fazer, mas que se está interessado em resolver. De um modo geral, entende-se como problema qualquer situação em que se perceba a insuficiência dos conhecimentos imediatos diante de um desafio, exigindo uma busca por estratégias que torne possível sua solução.
Meneghetti e Redling (2012) ressalta que, com a metodologia resolução de problemas aumenta-se a interação entre professor-aluno e aluno-aluno, promovendo um ambiente rico para aprender matemática.
Deste modo, Dante (2003) destaca que os objetivos da resolução de problemas são: (a) fazer o aluno pensar produtivamente, (b) desenvolver o raciocínio, (c) ensinar o aluno a enfrentar situações novas, (d) dar ao aluno a oportunidade de se envolver com as aplicações da matemática, (e) tornar as aulas de matemáticas interessantes e desafiadoras, (f) equipar o aluno com estratégias de resolução e, (g) proporcionar-lhes uma boa base matemática.
Porém, visando uma forma de orientar os professores a empregar esta metodologia em sala de aula, tornando-a mais dinâmica (participativa) e fazendo com que os alunos estudem a matemática com um olhar mais entusiástico e confiante, Polya (1978) implementou uma heurística para se trabalhar com resolução de problemas, composta de quatro etapas: (a) primeiramente, deve-se destacar as informações mais importantes do problema a ser resolvido, (b) após, elaborar um plano de resolução, (c) executar o plano e (d) conferir o resultado; se necessário, (e) estabelecer uma nova estratégia (até chegar a uma solução aceitável). Posteriormente, no trabalho de Allevato e Onuchic (2008), Onuchic e Allevato (2011), verifica-se uma nova versão, composta de nove etapas: (a) deve-se preparar o problema a ser resolvido, (b) deve-se fazer uma leitura individual, (c) deve-se fazer uma leitura em conjunto, (d) executar – resolver o problema, (e) observar e incentivar, (f) fazer registros durante a resolução do problema, (g) fazer uma plenária (discussão), (h) buscar o consenso e (i) formalizar o conteúdo.
Vale ressaltar que, o professor deve administrar essas etapas (processos), proporcionando situações que permitam surgir questionamentos, interações e motivação; o objetivo é dar ênfase a resolução e não à obtenção imediata da resposta correta. Sendo assim, é de suma importância que os professores compreendam como trabalhar esta metodologia, a fim de desenvolver no aluno a capacidade de resolver situações desafiadoras, interagir entre os pares, desenvolver a comunicação, a criatividade e o senso crítico.
Segundo Smole e Diniz (2001) cabe ao professor assegurar um espaço de discussão no qual os alunos pensem sobre os problemas que irão resolver, elaborem uma estratégia, apresentem suas hipóteses e façam o registro da solução encontrada ou de recursos que utilizaram para chegarem ao resultado. Isso favorece a formação do pensamento matemático, livre do apego às regras. O aluno pode lançar mão de recursos como a oralidade, o desenho e outros, até se sentir à vontade para utilizar sinais matemáticos.
A dinâmica nesta metodologia é de um trabalho centrado no aluno, onde ele possa desenvolver sua aprendizagem, construir seu conhecimento, onde o professor apenas mediará essa construção. Para Onuchic e Allevato (2005) trata de uma atividade onde o problema é o ponto de partida e orientação para a aprendizagem e, a construção do conhecimento far-se-á através de sua resolução, realizada de forma colaborativa entre professor e alunos.
Como reflexão do que foi apresentado nesta seção, apontamos que, se durante a vida escolar forem dadas oportunidades aos alunos de se envolverem com diferentes situações-problema (utilizando-se da metodologia resolução de problemas), quando adultos agiram com inteligência e naturalidade ao ter que enfrentar seus problemas da vida cotidiana, sejam eles de ordem econômica, política e social.
O BOLEMA (Boletim de Educação Matemática) é uma das mais importantes revistas na área da Educação Matemática no Brasil. Surgiu em 1985 por um grupo de pós-graduandos do Programa de Pós-Graduação em Educação Matemática da UNESP de Rio Claro (SP), sendo as primeiras edições publicadas neste mesmo ano.
A partir de 2008, com a intensão de aumentar a divulgação das produções científicas na área de Educação Matemática e afins, o BOLEMA passou a realizar suas edições de forma quadrimestral, recebendo trabalhos em fluxo contínuo. Os trabalhos publicados são artigos, ensaios, resenhas e resumos de dissertações e teses cujos focos relacionam-se ao ensino e à aprendizagem de Matemática e/ou ao papel da Matemática e da Educação Matemática na sociedade. Alguns destes trabalhos são resultados de pesquisas empíricas.
O BOLEMA, é considerado um periódico nacional, composta por um corpo editorial de renome, com integrantes do país e do exterior, sendo avaliado pela CAPES como periódico Qualis Nacional A1.
O estudo em questão trata-se de uma pesquisa do tipo revisão da literatura, o qual consiste na aplicação de estratégias que limitam o viés de seleção dos artigos, sintetizando os estudos mais relevantes em um único tópico. Portanto, algumas etapas se fizeram necessário (adaptado de TORRES, COSTA & LOURENÇO, 2016):
Etapa 1 (Definição da Pergunta): A primeira etapa consiste na elaboração da pergunta norteadora para a revisão: Quais as contribuições que a metodologia Resolução de Problemas pode trazer aos alunos, durante o processo de ensino e aprendizagem?
Etapa 2 (Busca dos Estudos): O levantamento bibliográfico acerca do tema de interesse foi realizado na base de dados da SciELO (Scientific Electronic Library Online) – biblioteca eletrônica cujo objetivo é proporcionar aos pesquisadores um amplo acesso à coleções de periódicos científicos, bem como, aos fascículos de cada título de periódico, assim como aos textos completos de artigos. Buscou-se pela SciELO por conter em sua base de dados, os “repositórios da revista BOLEMA” (foco da presente pesquisa), estando disponível para consulta apenas os artigos compreendidos entre o período de 2012 a 2017.
Como descritor, utilizou apenas a terminologia Resolução de Problemas. Os critérios de inclusão dos estudos foram: (a) artigos pertencentes ao período de 2012 a 2017, (b) estudos empíricos que apresentam e avaliam o método Resolução de Problemas e (c) artigos publicados na língua portuguesa e inglesa. Foram excluídos da amostra artigos que não eram empíricos e que não abordavam a metodologia resolução de problemas. As buscas ocorreram durante o mês de “setembro do ano de 2017”.
Etapa 3 (Coleta de Dados): Foram encontrados no total 11 artigos por meio da Scientific Electronic Library Online (SciELO), os quais podem ser vistos na página, http://www.scielo.br/cgi-bin/wxis.exe/iah/. Os artigos encontrados foram salvos, e então, deu-se início a seleção da amostra da revisão. Nesta etapa, todos os títulos e resumos foram lidos. Esse percurso resultou na exclusão de 04 artigos por não atenderem aos critérios de inclusão e aos propósitos da temática em questão. Ao final, sobraram 07 trabalhos, sendo todos lidos na íntegra, perfazendo uma segunda seleção. Todos foram aceitos. A Figura 1, apresenta um fluxograma que sintetiza o processo de obtenção da amostra de artigos incluídos nessa revisão.
Figura 1
Síntese do procedimento para obtenção da amostra da revisão.
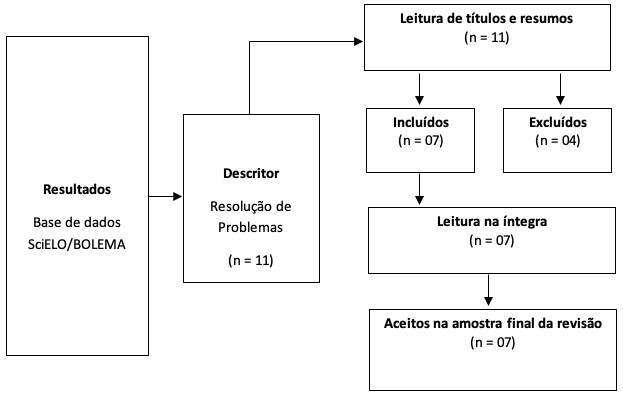
Fonte: Elaborado pelo autor
Nas próximas seções, esses 07 (sete) artigos selecionados para compor a revisão serão sintetizados e discutidos.
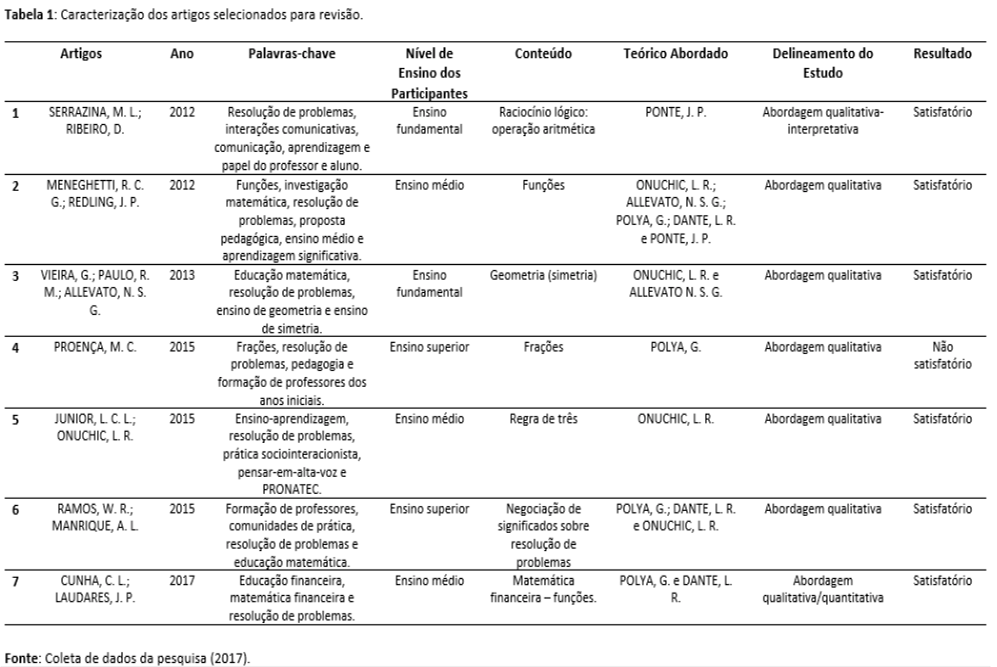
A Tabela 1 apresenta as principais informações extraídas dos artigos de acordo com o objetivo do estudo: revisão da literatura. Nota-se que, de acordo com os critérios utilizados na seleção da presente amostra, foram encontrados apenas artigos nacionais.
Por se tratar de uma pesquisa qualitativa (voltada especificamente à artigos submetidos na revista BOLEMA, entre 2012 a 2017, sobre a Metodologia Resolução de Problemas); serão sintetizadas as palavras-chave, número de trabalhos publicados, conteúdo trabalhado, teóricos abordados, procedimento de coleta de dados e resultados.
Pelas palavras-chave (ver Tabela 1), todos os trabalhos estão relacionados com a metodologia resolução de problemas para o ensino e aprendizagem de matemática, sendo cada um com sua peculiaridade, uns verificando a versatilidade desta metodologia em sala de aula, outros relacionado a formação de professores e outro, relacionado a própria metodologia. Todos os trabalhos discorrem de aplicações práticas (empíricos).
Na Tabela 2, temos o número de trabalhos publicados entre 2012 a 2017.
Tabela 2
Número de trabalhos publicados por ano na revista
BOLEMA sobre a Metodologia Resolução de Problemas.
Ano |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
No de trabalhos publicados |
02 |
01 |
-- |
03 |
-- |
01 |
No que se refere ao ano de publicação, dos 07 estudos, dois foram publicados em 2012, um em 2013, três em 2015 e um em 2017. Em 2014 e 2016 não houve publicação sobre a metodologia resolução de problemas. Podemos considerar que, a média de publicação entre 2012 a 2017 sobre o tema, é consideravelmente baixo, resultando em média 1,16 publicação por ano. Talvez, este baixo índice vem da inexperiência e dificuldade dos professores em se adequar a este tipo de metodologia, como pode ser visto em Proença (2015).
Os conteúdos trabalhados, relacionados respectivamente, ao seu nível de ensino, pode ser visto na Tabela 3.
Tabela 3
Conteúdo versus Nível de Ensino.
|
Ensino Fundamental |
Ensino Médio |
Ensino Superior |
Regra de Três |
|
X |
|
Raciocínio Lógico |
X |
|
|
Fração |
|
|
X |
Funções |
|
X |
|
Geometria |
X |
|
|
Matemática Financeira |
|
X |
|
Metodol. Res. de Problemas |
|
|
X |
Observa-se que, 02 artigos trabalharam com alunos do ensino fundamental (abordando raciocínio lógico e geometria), 03 trabalharam com alunos do ensino médio (abordando regra de três, funções e matemática financeira) e, os outros 02 artigos trabalharam com graduandos e professores pertencentes ao nível superior (abordando frações e a própria metodologia resolução de problemas). Observa-se que este método, pode ser aplicado em todos os níveis de ensino.
Quantos aos clássicos pesquisadores sobre a metodologia resolução de problemas, os mais mencionados na fundamentação teórica dos artigos analisados, foram (Tabela 4):
Tabela 4
Importantes pesquisadores presentes na
fundamentação teórica dos artigos.
|
Pesquisadores/Teóricos sobre a Metodologia Resolução de Problemas |
||||
Artigos analisados |
ALLEVATO, Norma Suely Gomes |
DANTE, Luiz Roberto |
ONUCHIC, Lourdes de La Rosa |
POLYA, George |
PONTE, João Pedro |
1 |
|
|
|
|
X |
2 |
X |
X |
X |
X |
X |
3 |
X |
|
X |
|
|
4 |
|
|
|
X |
|
5 |
|
|
X |
|
|
6 |
|
X |
X |
X |
|
7 |
|
X |
|
X |
|
1 - SERRAZINA, M. L.; RIBEIRO, D. (2012);
2 - MENEGHETTI, R. C. G.; REDLING, J. P. (2012);
3 - VIEIRA, G.; PAULO, R. M.; ALLEVATO, N. S. G. (2013);
4 - PROENÇA, M. C. (2015);
5 - JUNIOR, L. C. L.; ONUCHIC, L. R. (2015);
6 - RAMOS, W. R.; MANRIQUE, A. L. (2015) e
7 - CUNHA, C. L.; LAUDARES, J. P. (2017).
Observa-se nas colunas que, os pesquisadores/teóricos mais mencionados foram POLYA, G. e ONUCHIC, L. R. (dos 07 artigos, 04 referenciaram os mesmos); seguidos de DANTE, L. R., ALLEVATO, N. S. G. e PONTE, J. P. Outros autores (de uma forma geral), também defensores desta metodologia, foram mencionados nos artigos, como: krutetskii (1976), Echeverría e Pozo (1988), Mayer (1992), Carvalho (1994), Pozo e Angón (1998), Ponte e Serrazina (2000), Sternberg (2000), Mandarino (2002), Bicudo (2005, 2010), entre outros. Vale mencionar que o artigo 2 (MENEGHETTI & REDLING, 2012) referenciou todos os teóricos presentes na Tabela 4.
O procedimento de coleta de dados utilizada pelos autores, para verificar se houve ou não a aprendizagem através da metodologia resolução de problemas, se deu através de entrevistas, observações, registros escritos, notas de campo, gravações e avaliações, conforme pode ser visto na Tabela 5.
Tabela 5
Procedimento de Coleta de dados para análise de aprendizagem.
Procedimento de Coleta de Dados para Análise |
|||||||
Artig.
|
Entrevistas |
Observações |
Registros escritos |
Notas de Campo |
Gravação áudio |
Gravação vídeo |
Avaliação |
1 |
X |
X |
X |
X |
X |
X |
|
2 |
|
|
X |
|
|
|
|
3 |
|
|
X |
|
|
|
|
4 |
|
|
|
|
|
|
X |
5 |
|
|
X |
|
|
|
|
6 |
|
X |
|
X |
X |
|
|
7 |
|
|
|
X |
|
|
|
1 - SERRAZINA, M. L.; RIBEIRO, D. (2012);
2 - MENEGHETTI, R. C. G.; REDLING, J. P. (2012);
3 - VIEIRA, G.; PAULO, R. M.; ALLEVATO, N. S. G. (2013);
4 - PROENÇA, M. C. (2015);
5 - JUNIOR, L. C. L.; ONUCHIC, L. R. (2015);
6 - RAMOS, W. R.; MANRIQUE, A. L. (2015) e
7 - CUNHA, C. L.; LAUDARES, J. P. (2017).
Sobre o procedimento de coleta de dados, apenas o artigo 4 - Proença (2015) – utilizou de avaliação; procedimento este, não muito utilizado nas atividades envolvendo a metodologia resolução de problemas. Segundo Costa e Allevato (2009) o processo de avaliação do aluno deve ser feito continuamente durante a resolução do problema. O motivo (provavelmente) da avaliação é que, a metodologia estava sendo aplicado em uma disciplina da turma de pedagogia, sendo como regra da instituição, a aplicação da avaliação escrita para análise de rendimento dos alunos.
Quanto aos resultados, dos sete trabalhos analisados, seis apresentaram resultados satisfatório, os quais ressaltam que o ensino e aprendizagem de matemática através da metodologia resolução de problemas trazem ganhos de aprendizagem no desenvolvimento das estratégias de resolução, sendo importantes para estimular a participação e criatividade do aluno em aula. Apenas um dos trabalhos (artigo 4 – Proença, 2015), apresentou resultado não satisfatório (não houve aprendizagem), motivo este, pela inexperiência dos participantes em trabalhar com frações, inexperiência na estratégia resolução de problemas e pelo método de avaliação aplicado aos participantes (avaliação escrita); critério este, que não pontuou a favor dos mesmos.
Por fim, foram extraídos dos artigos, alguns parágrafos que demonstram a “efetividade” das práticas de Resolução de Problemas:
[...] As interações ocorridas com a abordagem da resolução de problemas na sala de aula, foram decisivas para os alunos se envolverem nas atividades, criarem um espírito investigativo e desenvolverem a capacidade de se comunicar (SERRAZINA, M. L.; RIBEIRO, D., 2012).
[...] As tarefas foram elaboradas levando-se em consideração a seguinte abordagem metodológica, à resolução de problemas. Verificamos que elas favorecem uma aprendizagem mais significativa aos alunos, permitindo-lhes maior compreensão sobre o assunto (MENEGHETTI, R. C. G.; REDLING, J. P., 2012).
[...] Na interpretação dos dados vimos que o ensino de simetria através da resolução de problemas potencializa a aprendizagem (VIEIRA, G.; PAULO, R. M.; ALLEVATO, N. S. G., 2013).
[...] Aluno Ignácio - A Resolução de Problemas foi muito boa para mim, porque consegui entender onde posso usar a matemática e, mais ainda, consigo pensar quando recebo um problema pela frente. Essa matemática é mesmo importante. [...] Neste discurso, gravado no último dia de aula, o professor percebeu o efeito da prática da Resolução de Problemas, como fator indispensável em suas aulas de matemática (JUNIOR, L. C. L.; ONUCHIC, L. R., 2015).
[...] O processo de conhecer e aprender como trabalhar com a estratégia de Resolução de Problemas foi considerado pelo grupo participante como parte importante da prática social do professor que ensina matemática (RAMOS, W. R.; MANRIQUE, A. L., 2015).
[...] Os resultados obtidos, resolução e interpretação, confirmaram a eficiência da metodologia empregada, evidenciando uma contínua melhora na postura reflexiva do estudante, para cálculos envolvendo matemática financeira (CUNHA, C. L.; LAUDARES, J. P., 2017).
Mediante estas “considerações”, deixa-se evidente a resposta para a pergunta de pesquisa: Quais as contribuições que a metodologia Resolução de Problemas pode trazer aos alunos, durante o processo de ensino e aprendizagem? Ou seja, verifica-se “nestas considerações” que as interações são importantes para envolver os alunos nas atividades, e que, a pratica da metodologia resolução de problema faz o aluno pensar, torna-o mais reflexivo e faz com que o aluno compreenda melhor o assunto. Além disto, verifica-se nas considerações que os alunos aconselham a prática desta metodologia pelos professores nas aulas de matemática.
Ensinar matemática é uma tarefa desafiadora para quem deseja alcançar o objetivo de inserir conhecimentos na formação do aluno, ou seja, é educar; e educar significa ajudar a desenvolver no aluno à curiosidade, a motivação, o gosto por aprender. Diante disso, se faz necessário práticas pedagógicas que tenham significados para os alunos, sendo o professor apenas o mediador da aprendizagem, ou seja, aquele que instiga o desenvolvimento da aprendizagem utilizando-se de estratégias/ferramentas que contribuam para a construção do conhecimento. Tal estratégia, analisada neste artigo, foi a “Metodologia via Resolução de Problemas”.
Assim, para o desenvolvimento deste trabalho e de acordo com os critérios utilizados para a seleção dos artigos, resultaram 07 artigos, os quais foram analisados. O período de pesquisa oscilou de 2012 a 2017, perfazendo uma média de 1,16 trabalhos por ano neste intervalo (pouco), extraído da base Scientific Electronic Library Online (SiELO) junto a revista BOLEMA.
Os artigos revisados mostram que essa metodologia tem potencial no processo de ensino e aprendizagem, uma vez que buscam engajar os alunos na dinâmica da aprendizagem; participando, colaborando, refletindo e, até mesmo, criando estratégias de pensamento para a resolução dos problemas; características estas, consideradas importantes, tanto na vida acadêmica dos alunos como na futura vida profissional. Os resultados apresentados pelos autores nesta revisão, mostram que essa metodologia traz benefícios no processo de aprendizagem (é satisfatório). Dos sete artigos analisados, apenas um mostrou-se não satisfatório (sem aprendizado), motivo este, pelo fato dos participantes estarem utilizando este método pela primeira vez, sendo o critério de avaliação utilizado pelo professor não usual para esta metodologia (avaliação escrita).
Verificou-se também que, o método pode ser aplicado em ambas as categorias de ensino, seja no fundamental, médio ou superior. Também, buscou-se apresentar os grandes pesquisadores na área (Tabela 4).
Enfim, neste trabalho, fez-se uma breve revisão (ou seja, um recorte) sobre o método resolução de problemas, pesquisando apenas os artigos submetidos na revista Bolema. Outras revistas poderiam ser analisadas como: ZDM Mathematics Education (ISSN 1863 9704), Acta Scientiae (ISSN 2178 7727), Amazônia (ISSN 2317 5125), Educação UFSM (ISSN 1984 6444), Educação, Matemática e Pesquisa (ISSN 1983 3156), etc. Outros trabalhos que mostram a aplicação e a eficiência desta metodologia nas aulas de matemática, também podem ser vistos em: Nunes & Santana (2017), Gomes, Barbosa & Concordino (2017), Palis, Augusto & Pitombeira (2017), Rodrigues, Santos & Souza (2016), Miranda (2015), Onuchic & Allevato (2014), Onuchic & Allevato (2011), Onuchic (1999), entre outras.
Espera-se que este trabalho, desperte a curiosidade nos docentes e futuros docentes, à pesquisarem, aprimorarem e aplicarem o método resolução de problemas nas aulas de matemática, tornando-a mais dinâmica e participativa, incentivando os alunos a ampliarem seus conhecimentos e o gosto por aprender matemática.
ALLEVATO, N. S. G.; ONUCHIC, L. R. Ensinando matemática na sala de aula através da resolução de problemas. 11º Congresso Internacional de Educação matemática. Monterrey - México. Realizado em julho de 2008. Disponível em: http://tsg.icme11.org/document/get/453. Último acesso em 20 set. 2017.
ALLEVATO, N. S. G; ONUCHIC, L. R. Ensino-Aprendizagem-Avaliação de Matemática: por que Através da Resolução de Problemas? In: ONUCHIC, L. R. et al. (Orgs.). Resolução de Problemas: Teoria e Prática. Jundiaí: Paco Editorial, 2014, p. 35-52.
BRASIL. MEC. Parâmetros curriculares nacionais: matemática. 1º, 2º, 3º e 4º ciclos. Ensino médio: matemática. Brasília, 1997, 1998, 1999.
COSTA, M. S.; ALLEVATO, N. S. G. Metodologia de ensino-aprendizagem-avaliação através da resolução de problemas: opiniões e reflexões de (futuros) professores de matemática. Disponível em: http://www.sinprosp.org.br/congresso_matematica/revendo/dados/files/textos/Sessoes/METODOLOGIA%20DE%20ENSINO-APRENDIZAGEM-AVALIA%C3%87%C3%83O%20ATRAV%C3%89S%20DA%20RESO.pdf. Acesso em 10 set. 2017.
CUNHA, C. L.; LAUDARES, J. B. Resolução de problemas na matemática financeira para tratamento de questões da educação financeira no ensino médio. Bolema, Rio Claro (SP), v. 31, n. 58, p. 659-678. 2017.
DANTE, L. R. Didática da resolução de problemas de matemática. São Paulo: Editora Ática, 2003.
DEMO, P. Educação e qualidade. Campinas: Papirus, 1996.
GOMES, D. A.; BARBOSA, A. C. C.; CONCORDINO, C. F. R. Ensino de matemática através da resolução de problemas: análise da disciplina RPM implantada pela SEEDUC-RJ. Revista EPM – Educação Matemática e Pesquisa, São Paulo, v. 19, n. 01, p. 105-120. 2017.
GOV. Governo do Paraná. Diretrizes curriculares da educação básica de matemática. Secretaria de estado da educação do paraná. 2008. Disponível em: <http://www.educadores.diaadia.pr.gov.br/arquivos/File/diretrizes/dce_mat.pdf>. Último acesso em 19 set. 2017.
JACINTO, H.; CARREIRA, S. Diferentes modos de utilização do geogebra na resolução de problemas de matemática para além da sala de aula: evidências de fluência tecno-matemática. Bolema, Rio Claro (SP), v. 31, n. 57, p. 266-288. 2017.
JUNIOR, L. C. L.; ONUCHIC, L. R. Ensino e aprendizagem de matemática através da resolução de problemas como prática sociointeracionista. Bolema, Rio Claro (SP), v. 29, n. 53, p. 955-978. 2015.
MENEGHETTI, R. C. G.; REDLING, J. P. Tarefas alternativas para o ensino e a aprendizagem de funções: análise de uma intervenção no ensino médio. Bolema. Rio Claro (SP), v. 26, n. 42ª, p. 193-229. 2012.
MIRANDA, A. S. M. S. Resolução de problemas como metodologia de ensino: uma análise das repercussões de uma formação continuada. Programa de Pós-Graduação em Educação em Ciências e Matemática. Dissertação de Mestrado. Pontifícia Universidade Católica do Rio Grande do Sul. 2015.
NUNES, C. B.; SANTANA, E. R. S. Resolução de problemas: um caminho para fazer e aprender matemática. Revista Acta Scientiae, Canoas, v. 19, n. 01, p. 2-19. 2017.
ONUCHIC, L. R. Ensino-aprendizagem de Matemática através da resolução de problemas. In: BICUDO, M. A.V. (Org). Pesquisa em Educação Matemática: Concepções & Perspectivas. Editora UNESP, São Paulo (SP), p. 199–218. 1999.
ONUCHIC, L. R.; ALLEVATO, N. S. G. Novas reflexões sobre o ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, M. A. V.; BORBA, M. C. (orgs). Educação matemática: pesquisa em movimento. 2 ed. p. 213-231. São Paulo: Cortez, 2005.
ONUCHIC, L. R., ALLEVATO, N. S. G. Pesquisa em resolução de problemas: caminhos, avanços e novas perspectivas. Bolema, Rio Claro (SP), v. 25, n. 41, p. 73-98. 2011.
PALIS, G. L. R.; AUGUSTO, A.; PITOMBEIRA, J. B. Resolução de Problemas. Projeto Matemática: Comunidade e Universidade. Departamento de Matemática e NEAM (Núcleo de estudo e ação sobre o menor). 2017.
POLYA, G. A arte de resolver problemas. Trad. Heitor Lisboa de Araújo. Rio de Janeiro: Editora Interciência, 1978.
PROENÇA, M. C. O ensino de frações via resolução de problemas na formação de futuras professoras de pedagogia. Bolema, Rio Claro (SP), v. 29, n. 52, p. 729-755. 2015.
RAMOS, W. R.; MANRIQUE, A. L. Comunidade de prática de professores que ensinam matemática como espaço de negociações de significados sobre resolução de problemas. Bolema, Rio Claro (SP), v. 29, n. 53, p. 979-997. 2015.
RODRIGUES, S. O.; SANTOS, S. S.; SOUZA, T. M. G. Metodologia de Resolução de Problemas: Uma prática viável para o ensino de matemática. III CONEDU – Congresso Nacional de Educação. 2016.
SERRAZINA, M. L.; RIBEIRO, D. As interações na atividade de resolução de problemas e o desenvolvimento da capacidade de comunicar no ensino básico. Bolema, Rio Claro (SP), v. 26, n. 44, p. 1367-1393. 2012.
SOARES, M. T. C.; PINTO, N. B. Metodologia da resolução de problemas. In: Anais eletrônicos - 24ª Reunião ANPED: Caxambu, 2001, p. 1-9. Disponível em: http://www.anped.Org.br/reunioes/24/tp1.htm#gt19. Último acesso em: 18 set. 2017.
SMOLE, K. S.; DINIZ, M. I. Ler, escrever e resolver problemas. Porto Alegre: Editora Artmed, 2001.
TORRES, J. P.; COSTA, C. S. L.; LOURENÇO, G. F. Substituição sensorial visuo-tatil e visuo-auditiva em pessoas com deficiência visual: uma revisão sistemática. Revista Brasileira de Educação Especial. Marília, v. 22, n. 4, p. 605-618. 2016.
VIEIRA, G.; PAULO, R. M.; ALLEVATO, N. S. Simetria no ensino fundamental através da resolução de problemas: possibilidades para um trabalho em sala de aula. Bolema, Rio Claro (SP), v. 27, n. 46, p. 613-630. 2013.
1. Doutorando em Ensino de Ciência e Tecnologia pela UTFPR-PG. Docente do Departamento Acadêmico de Física, Estatística e Matemática da UTFPR-FB. Área de atuação – Ensino de Matemática. E-mail renatohallal@utfpr.edu.br
2. Doutora em Educação Científica e Tecnológica pela UFSC. Docente do Programa de Pós-Graduação em Ensino de Ciência e Tecnologia da UTFPR-PG. Área de atuação – Ensino de Matemática e Educação Científica e Tecnológica.
3. Mestre em Engenharia de Produção pela UFSCar. Docente do Departamento de Engenharia de Produção da UNIRP. Área de atuação – Sistemas de Informação
4. Doutora em Estatística e Experimentação Agronômica pela ESALQ/USP. Docente do Departamento Acadêmico de Física, Estatística e Matemática da UTFPR-FB. Área de atuação – Análise Estatística de Dados