ISSN 0798 1015

Vol. 39 (Nº 51) Año 2018. Pág. 11

Aplicación de la simulación Monte Carlo en la proyección del estado de resultados. Un estudio de caso

Application of the Monte Carlo simulation in the projection of statement of profit or loss. A case study

Erika Janeth SALAZAR Jiménez 1; Wilmar Alexander ALZATE Castro 2

Recibido: 10/07/2018 • Aprobado: 25/09/2018 • Publicado 22/12/2018

Contenido

1. Introducción

2. Simulación Monte Carlo: definición, ventajas y limitaciones en su aplicación al mundo de los negocios

3. Condiciones de la información financiera para utilizar SMC en la proyección del estado de resultados

4. Construcción de la SMC

5. Metodología en la construcción del modelo

6. Hallazgos y conclusiones

Referencias bibliográficas

1. Introducción

En el mundo de los negocios, las organizaciones empresariales ejecutan sus actividades en medio de las interacciones con los demás agentes económicos conocidos como stakeholders. La información que se genera producto de estas relaciones organizacionales es sistematizada y resumida en un conjunto de informes que contribuyen a la toma de decisiones, tales como: optimizar recursos, evitar despilfarros, programar producción, definir estrategias de mercado, analizar riesgos, entre otros.

Con base en la información histórica y en el diagnóstico de su situación actual, las organizaciones requieren anticipar sus resultados como una valiosa herramienta para la administración y el uso de sus recursos. Por esta razón, la proyección de estados financieros es una importante labor que requiere de la consideración de diferentes elementos conocidos y desconocidos, pues en condiciones de incertidumbre, la gestión del riesgo es un factor clave en el éxito de las organizaciones.

La simulación Monte Carlo es un método que combina el uso de los sistemas de información organizacional (información histórica principalmente) y la aleatoriedad para estimar la posibilidad de ocurrencia de un evento. Aplicando este método para proyectar los estados financieros, la administración de una organización puede reconocer la probabilidad de ocurrencia de escenarios deseables o no deseables, con el fin de tomar acciones sobre las variables que puede controlar.

Aplicar la simulación Monte Carlo requiere la identificación de las variables claves que afectan el resultado a proyectar, así como la distribución de probabilidad que defina el comportamiento de estas variables.

Esta investigación pretende resaltar el uso de la simulación Monte Carlo como herramienta poderosa de la administración para la gestión estratégica de sus recursos en el corto plazo, en especial, de las variables que afectan el resultado del periodo: ingresos, costos y otros gastos. De esta manera, con base en un análisis de sensibilidad sobre el resultado del periodo, se podrá identificar las probabilidades de ocurrencia de un escenario no favorable, uno optimista y el más probable.

Por lo tanto, el escrito pretende describir el uso de la simulación Monte Carlo en el ámbito de los negocios como un método que contribuye a la gestión de los costos para la toma de decisiones empresariales. También se presentan los requerimientos de información de los sistemas de costos, las ventajas y las limitaciones de la aplicación de dicha simulación en la proyección de la información financiera. Por último, se presentarán los hallazgos y conclusiones derivados de un estudio de caso en la construcción de múltiples escenarios de un estado de resultados en una empresa prestadora de servicios de testing de software.

Las simulaciones tienen el objetivo de duplicar características y comportamientos propios de un sistema real, es decir, imita el comportamiento de un sistema a través de la manipulación de un modelo que representa la realidad. (Rodriguez, 2011) La simulación Monte Carlo (SMC) no es ajena al anterior objetivo, y tiene una característica primordial: permite simular el comportamiento de las variables que inciden en el problema a analizar, cuando se tiene incertidumbre sobre el comportamiento que éstas van a tener y su efecto sobre la variable dependiente, esto a través de una técnica de base científica que brinde mayor soporte a las proyecciones futuras. (Lledó & Rivarola, 2007, pág. 394)

La simulación Monte Carlo es una técnica cuantitativa que permite el desarrollo de un modelo lógico-matemático del que se obtienen la imitación de un proceso del sistema a través del tiempo. Por lo tanto, la simulación involucra la generación de una historia artificial del sistema y la observación de esta historia mediante la manipulación experimental; además, ayuda a inferir las características operacionales de tal sistema. (Azofeifa, 2004). El término SMC proviene por su similitud al muestro aleatorio en los juegos de ruleta en los casinos de Monte Carlo.

La SMC reproduce los valores de una variable a partir de su comportamiento, basado en la selección de números aleatorios para las variables independientes que le afectan, considerando sus distribuciones de probabilidad (Lledó & Rivarola, 2007, pág. 396). Para poder aplicar la SMC, es necesario contar con suficiente información histórica, que permita establecer cómo se comportan las variables y cómo éstas afectan o son afectadas por otras variables. (Chase & Jacobs, 2014)

Los modelos de SMC suelen enfocarse en operaciones detalladas en un sistema, ya sean físicas o financieras. En este sistema se estudia la manera cómo funciona a través del tiempo y se incluyen los efectos de los resultados de un periodo sobre el siguiente. (Azofeifa, 2004) Es así que, la SMC al generar una historia artificial o una reproducción del comportamiento de una variable, puede brindar información sobre situaciones de incertidumbre como: ¿cuántas unidades posiblemente se venderán el próximo mes? ¿cuál es la probabilidad de obtener utilidad en el próximo período? ó ¿cuál es la variable que tiene mayor impacto sobre la utilidad del período? (Vergara Schmalbach, 2005)

La SMC proporciona soluciones aproximadas a una gran variedad de problemas matemáticos posibilitando la realización de experimentos con muestreos de números pseudoaleatorios en una computadora. El método es aplicable a cualquier tipo de problema, ya sea estocástico o determinista. (Velásquez & Velásquez, 2012)

Esta herramienta se ha aplicado en diferentes ámbitos, tales como la ingeniería, la biología, las telecomunicaciones, la investigación y desarrollo, entre otros. Según Vannelle, Lucato, Viera y Sato (2012), Cruz (2012) y Mancilla (1999), en las finanzas, la economía y los negocios, las aplicaciones más significativas se han dado en términos de la gestión de proyectos financieros, el cálculo del valor de la empresa, la construcción de escenarios financieros, la evaluación de decisiones de inversión de la empresa o de los derivados financieros, incluso para identificar dificultades y proponer acciones correctivas en una línea de producción en marcha, determinar políticas de ordenamiento en un sistema de inventario y otros sistemas de producción. Asimismo, la evaluación de la introducción de un nuevo producto al mercado y el cálculo del tiempo de espera en la prestación de un servicio, son decisiones que se pueden basar en los resultados de la SMC. Autores como Wiedemann, Hager y Roehrl (2003) citados por Flórez y Moscoso (2009) indican que el uso de procesos estocásticos como la SMC pueden simular los desempeños a través del tiempo de tasas de interés, tasas de cambio, precios de materias primas y precios de activos financieros, así como el desempeño de variables operacionales como ingresos y volúmenes de ventas, ganancias corporativas y flujos de caja, entre otros.

El proceso de simulación permite construir las distribuciones de probabilidad para todo tipo de indicador financiero, lo que hace posible realizar un análisis bajo riesgo de cualquier aspecto de la empresa, esto es, que sería posible trasladar el análisis financiero tradicional realizado en términos determinísticos a un ambiente de incertidumbre. (Medina & Restrepo, 2013). Por lo anterior, muchos teóricos indican que la SMC es un gran apoyo para la gestión de los riesgos en las organizaciones, ya que no solo brinda el valor más probable sino también, la ventana de todos los resultados posibles que pueden ser analizados a través de su distribución de probabilidad. (Lledó & Rivarola, 2007, pág. 401)

Otras ventajas de la SMC son: identificar a través de sus predicciones el grado de sensibilidad de las variables independientes o de entrada con la variable dependiente o de salida. En la medida en que se identifique la variable independiente más sensible a la variable dependiente, la compañía podrá hacer mejor control sobre esas variables sensibles para que los resultados finales sean similares a los esperados o deseables (Mancilla H., 1999).

Es importante reconocer que esta herramienta puede generar una gran cantidad de escenarios en los cuales se puede ajustar el resultado final, por lo tanto, otorga un rango muy amplio de posibilidades que requieren del análisis de información complementaria cuantitativa y cualitativa que permita delimitar más el escenario en el que se puede encontrar la empresa en el corto plazo.

En relación a desventajas de la utilización de la SMC, Rodríguez (2011) nos relaciona las siguientes:

• Un gran número de variables hace una buena simulación, pero resulta complicada sino se tiene una herramienta tecnológica.
• La simulación no genera situaciones o soluciones óptimas, como maximizar utilidades o minimizar costos.
• Cada simulación es única por intervenir el azar.

La simulación Monte Carlo no se ha diseñado para encontrar la mejor solución o soluciones óptimas, como en la programación lineal o en análisis de decisiones, sino que evalúan diferentes alternativas y se toma una decisión con base en una comparación de los resultados. Es decir, se evalúa el desempeño de sistemas previamente especificados. (Azofeifa, 2004)

Los resultados de una organización son el efecto de relacionar los ingresos o incrementos patrimoniales menos los costos y los gastos o disminuciones patrimoniales, producto de las operaciones ordinarias o extraordinarias, diferentes a los aportes de los socios y a los rendimientos de estos aportes. Este esquema normalmente se presenta dentro del estado financiero denominado Estado de Resultados. (Duque, Muñoz, & Osorio, 2011)

e acuerdo a los estándares internacionales de información financiera – IFRS, los resultados de la organización provienen no solo de las actividades ordinarias, sino también de otras actividades asociadas con la estructura de inversión y de financiación de la compañía. La NIC 1, establece que el rendimiento de la organización se compone del resultado del periodo y de otros resultados integrales, los cuales pueden presentarse de forma conjunta o separada. El resultado del periodo corresponde a la diferencia entre los ingresos y gastos realizados en el periodo, mientras que los otros resultados integrales (ORI) son partidas de ingresos y gastos no realizados, cuyo efecto en la estructura financiera de la empresa se verá en el futuro ya sea en el resultado del periodo o directamente en la cuenta de ganancias acumuladas en el patrimonio. (IFRS Foundation, 2015)

Para efectos del presente trabajo, se excluye del alcance de la investigación las partidas del ORI, debido a que su naturaleza es incierta en función del comportamiento del valor razonable, la tasa de cambio y otras variables inmersas en los cálculos actuariales, por lo que no dependen de las variables aleatorias que se trabaja en el modelo de la simulación Monte Carlo que son los niveles de producción y ventas de una organización.

El estado de resultado es un informe importante para los empresarios, pues a partir de él evalúan las utilidades que arroja las operaciones de la organización mes a mes y el desempeño de la administración del negocio, sólo por mencionar algunos. Por lo tanto, los tomadores de decisiones en las compañías están a la espera que en el futuro los resultados sean positivos y cumpliendo un nivel de rentabilidad deseado por los inversionistas. Esto genera inquietudes como: ¿cuál es la probabilidad de que en el próximo período se cumplan las utilidades deseadas? ¿cuáles son las variables que más inciden en la generación de los resultados esperados?. Inquietudes cómo estas pueden ser resueltas con la SMC aplicada al estado de resultados, pues estos interrogantes están bajo situaciones futuristas y por ende con un grado de incertidumbre.

Cualquiera de las dos formas básicas para presentar el estado de resultados según los lineamientos de las IFRS, es decir, por naturaleza o por función, son limitadas para la aplicación de la simulación Monte Carlo, pues no refleja para todas las partidas empleadas en el cálculo de la utilidad cuáles en el futuro cercano (corto plazo) tiene un comportamiento bajo incertidumbre y cuáles no. Por lo tanto, es necesario realizar unas clasificaciones adicionales de los rubros usados en el estado financiero aplicando el modelo costo-volumen-utilidad (CVU).

Recuérdese, que a partir de la teoría del modelo costo-volumen-utilidad los ingresos, costos y gastos tienen un comportamiento variable, fijo o semivariable en relación a los niveles de producción y venta. A continuación, se relacionan las definiciones de los conceptos anteriores con la estadística, para identificar en qué aporta a esta teoría en la determinación de las distribuciones de probabilidad para aplicar la SMC.

Un costo variable es un costo que cambia en su total en la proporción de los cambios en el nivel relacionado del volumen de producción o de la actividad total, (Horngren, Datar, & Foster, 2007) y cuyo costo unitario permanece constante dentro un rango relevante y en el corto plazo. (Polimeni, Fabozzi, Adelberg, & Arthur, 1994) En la Figura 1 se muestra que los costos variables tienen una relación lineal con el nivel de operación, pues si no hay producción no hay costo variable, y si hay mucha producción el costo variable es alto.

Figura 1
costos variables totales y unitarios

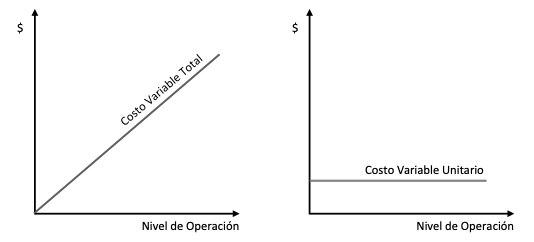
Fuente: Cuervo, et. al. (2013)

Por su parte los costos fijos permanecen constantes durante un período de tiempo determinado o para cierto nivel de capacidad de producción. (Laporta, 2014) Los costos fijos se consideran como tal en su monto global, pero unitariamente varían en forma inversa con la producción (Polimeni, Fabozzi, Adelberg, & Arthur, 1994), es decir, el costo fijo unitario se considera variables como muestra la Figura 2.

Figura 2
costos fijos totales y unitarios

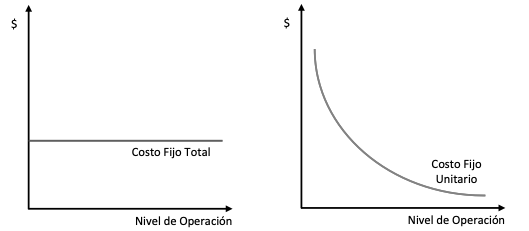
Fuente: Cuervo, et. al. (2013)

También existen los costos semivariables o semifijos, que se componen de una parte fija y otra variable que se modifica de acuerdo al volumen de producción. Hay dos tipos de costos semifijos o semivariables: mixtos y escalonados. Los primeros tienen una porción fija básica y a partir de ésta comienza a incrementar. Los segundos, permanecen fijos de acuerdo con el comportamiento de una variable, es el caso de la supervisión, esta permanece fija de acuerdo con el número de trabajadores. (Cuervo, Osorio, & Duque, 2013) La Figura 3 ilustra el comportamiento gráfico de estos costos.

Figura 3
costos semifijos mixtos y escalonados

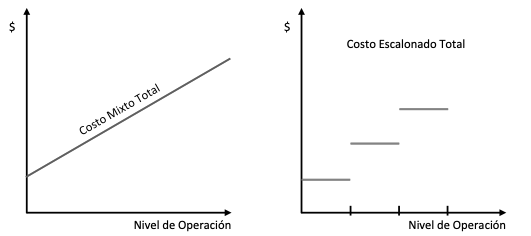
Fuente: Cuervo, et. al. (2013)

Algunas veces es fácil identificar los componentes variables y fijos de un costo semifijo, como cuando a un vendedor se le paga un salario base y unas comisiones por las unidades que venda. Sin embargo, en la mayoría de las ocasiones, la única información disponible es el costo total del recurso y una medida del producto final asociado a ese recurso. (Hansen & Mowen, 2007). Por ejemplo, un sistema contable por lo general registrará el costo total de mantenimiento para un período, porque con frecuencia se registra simplemente el total sin ningún intento de segregar los costos fijos y variables o simplemente el documento soporte del hecho económico no refleja dicha segregación. (Osorio, Alzate, & Agudelo, 2016) Para segregar la parte fija y variable de un costo existen varios métodos: punto alto y punto bajo, gráfico de dispersión y el método de los mínimos cuadrados.

Se ha mencionado que la SMC es un método para análisis bajo incertidumbre porque permite trabajar procesos estocásticos , por lo tanto, contempla variables aleatorias o estocásticas, esto son variables que toman valores numéricos realizados por los resultados contenidos en el espacio muestral generado por un experimento aleatorio, (Newbold, Carlson, & Thorne, 2013) es decir, su valor está determinado por el azar.

Lo anterior se relaciona con los conceptos de costos variables y la parte variable de los semifijos totales, en la medida que estos costos tienen dos componentes que para análisis futuros sólo uno de ellos está bajo incertidumbre. El componente que hace referencia al volumen de producción o actividad (unidades producidas, horas hombre, horas máquina, kilos transformados, unidades vendidas, etc.) es el que le da un comportamiento variable a este tipo de costos, por lo tanto, es una variable no determinística, que conocer su valor en el futuro es incierto, y es a esta variable la que se requiere conocer su distribución de probabilidad para aplicar la SMC. El otro componente es el valor monetario de una unidad del componente físico o del volumen de producción, es decir, el costo variable unitario; que bajo la teoría del CVU este componente se considera fijo y conocido en el corto plazo.

Por su parte, los costos fijos y la parte fija de los costos semivariables de manera total, son costos que sólo tienen un componente: el monetario, el cual no está relacionado con los volúmenes de producción. Por lo tanto, bajo un escenario de corto plazo, el costo fijo es un valor conocido en el futuro cercano y no le aplica distribución de probabilidad, es decir, no es una variable aleatoria.

En conclusión, para la aplicación de la SMC en el estado de resultados, en primera instancia se debe realizar la clasificación del comportamiento de los ingresos, costos y gastos en fijos, variables y semifijos. Para estos últimos se debe proceder aplicar algún método de separación en su componente fijo y variable. Solamente para las partidas de volumen de producción o venta se debe identificar la distribución de probabilidad, si se está bajo escenarios de corto plazo.

De acuerdo a Vélez (2003), Jorion (2006), Molina (2011) y Medina y Restrepo (2013) los pasos a seguir para la aplicación de la simulación Monte Carlo; adaptados para la construcción del modelo de decisión el Estado de Resultados, son los siguientes:

• Identificar para cada una de las variables estocásticas las distribuciones de probabilidad con sus debidos parámetros. Esto son los volúmenes de producción o de venta por tipo de servicio o producto.
• Calcular las correlaciones entre las variables independientes. Incluir posibles dependencias entre las variables.
• Construir el modelo para proyectar el Estado de Resultados, donde se presenten las relaciones matemáticas entre los ingresos, costos, gastos y unidades vendidas para calcular los diferentes tipos de utilidad y la contribución marginal.
• Generar números aleatorios o pseudoaleatorios.
• Alimentar los procesos estocásticos o las distribuciones de probabilidad inversas con los números aleatorios.
• Calcular el número de simulaciones. Entre más grande sea la cantidad de simulaciones es mejor, esto basado en la ley de los grandes números. Cada corrida es un escenario posible y consistente basado en los supuestos establecidos en el modelo. Cada resultado debe ser guardado.
• Realizar el análisis de estadística descriptiva, esto es: calcular la media, la varianza, la probabilidad de que el resultado asuma ciertos valores, histograma, entre otros.
• Hacer un análisis de sensibilidad, Puede ayudarse con el gráfico de tornados para identificar cual variable independiente del modelo al tener un cambio es la que más afecta la variable dependiente.

Entre los análisis más importantes a la hora de construir modelos de simulación figuran los análisis de sensibilidad, que permiten medir el efecto de los factores de riesgo sobre las utilidades. (Medina & Restrepo, 2013) Debido a su importancia para la creación de escenarios con base en la probabilidad de ocurrencia de los resultados, se espera que la simulación Monte Carlo sea una poderosa herramienta para la proyección de los resultados financieros de las organizaciones en tres condiciones básicas de los análisis de sensibilidad: primero el escenario de normalidad o el más probable, segundo el escenario de adversidad o el más negativo, y por último el escenario óptimo, próspero o el más positivo.

Dado las herramientas computacionales que se tienen hoy disponibles en el medio, ejecutar los pasos anteriores es sencillo. La SMC se puede realizar solamente con Excel siempre que las distribuciones de probabilidad de las variables independientes están parametrizadas como funciones en dicha aplicación, tal como ocurre en el estudio de caso a presentar, de lo contrario, se recomienda utilizar complementos de Excel como es el caso del @risk, el Cristal Ball o el Sens It, o softwares estadísticos como el Statgraphics, Minitab, Stata, entre otros.

Cómo se mencionó en la introducción, el estudio de caso es aplicado a una empresa que presta el servicio de testing de software, particularmente cinco tipos de pruebas con las siguientes convenciones: de alta automatización (S1), de automatización clásica (S2), contables (S3), funcionales (S4) y de performance (S5). La empresa cuenta con un sistema de costos que realiza la clasificación de sus recursos en variables, fijos y semivariables, donde a estos últimos les aplica el método de los mínimos cuadrados para separar el costo en sus componentes fijo y variable. Igualmente clasifica los costos y gastos fijos en identificables por servicio y no identificables. Los primeros son asignados a cada servicio, los segundos se asigna a nivel corporativo y no se distribuyen por servicio.

A continuación, se describe los pasos para la configuración del modelo y hallazgos de la aplicación de la SMC:

Paso 1 variables independientes y sus distribuciones de probabilidad. La empresa tiene creada 177 cuentas contables de costos y gastos, de las cuales sólo 33 se consideran en el análisis, pues se utilizó un Pareto para determinar cuáles cuentas contables representan el 94% de los costos. De las 33 cuentas, 22 cuentas presentan un comportamiento variable o semivariable. La empresa objeto de estudio suministró el costo variable unitario de estas cuentas y un historial de 30 meses del tiempo de prestación del servicio por cada uno de los tipos de servicios mencionados. Siguiendo los supuestos del modelo CVU, sólo al componente volumen de producción se le realizaron las pruebas de bondad de ajuste con el criterio Anderson-Darling, en la Tabla 1 se presenta la distribución de probabilidad y los parámetros para cada variable y se utilizó la aplicación @risk para realizar las pruebas de bondad de ajuste.

Para las cuentas que tienen un comportamiento fijo, se utilizó como valor determinístico el valor monetario definido por la compañía en su sistema de costos por mes (CTF costo total fijo o GTF gasto total fijo) al igual que el costo variable unitario en función de una hora de prestación de servicio (CUV costo unitario variable o GUV gasto unitario variable). En las tablas 2 y 3, se presenta el resumen de los anteriores datos.

Tabla 1
D istribuciones de probabilidad y sus
parámetros de las variables estocásticas

Fuente: elaboración propia a partir de @risk

-----

Tabla 2
Variables determinísticas identificables por servicio

Fuente: elaboración propia a partir de los datos del estudio de caso

------

Tabla 3
Variables determinísticas generales no identificables por servicio

Fuente: elaboración propia a partir de los datos del estudio de caso

Paso 2 calcular las correlaciones entre las variables independientes. La definición de un costo variable es que cambia si hay cambios en la producción, es decir, que debe existir una correlación entre las 22 cuentas contables y las variables tiempo del personal en la prestación del servicio. El coeficiente de correlación en modelos lineales es una forma de medir la existencia de correlación entre las variables mencionadas, pues mide la intensidad de la relación lineal entre las variables del costo total (cuenta contable) y el nivel de operación (tiempo del personal en la prestación del servicio). (Gutiérrez & de la Vara, 2008). Se verificó que las 21 cuentas presentan correlación positiva con el tiempo del personal en la prestación del servicio, aunque el valor en muchos casos no alcanza el valor mínimo de 0,6 para el coeficiente.

Paso 3 construir el modelo a proyectar. El modelo de proyección construido fue un Estado de Resultados bajo el método marginal, pues como se indicó en incisos anteriores, es necesario clasificar los costos en fijos y variables para la aplicación de la SMC. El Estado de Resultados por el método marginal es aquel que detalla los costos fijos y variables de un período. En la Tabla 4 se presenta un escenario como ejemplo.

Paso 4 generar números aleatorios. Dado que las variables aleatorias son el tiempo de prestación del servicio por tipo de servicio, se requería la generación de seis números aleatorios por corrida o escenario. Los números aleatorios se generaron con la función de Excel ALEATORIO.

Paso 5 alimentar los procesos estocásticos. El número aleatorio se emplea como la probabilidad de ocurrencia de un evento, por lo tanto, al ingresar dicha probabilidad en la distribución correspondiente ésta arroja el valor de la variable que cumpla esa distribución. En la Tabla 5, se presenta la función de Excel que permite hallar cada variable aleatoria que se utilizó como unidad de medida las horas o la fórmula de cálculo, en el caso de la distribución triangular, no existe la respectiva función en Excel. La denotación  es para el número aleatorio y  para las horas de prestación del servicio en un mes.

Paso 6 calcular el número de simulaciones. La cantidad de simulaciones a realizar puede ser un dato escogido por el analista, que, apoyado en la teoría de los grandes números, entre más simulaciones contemple mejor estimación se tendrá de los valores muestrales. Para el estudio de caso se realizaron 2.730 simulaciones. El analista también puede aplicar alguna de las técnicas que se tienen en estadística para determinar el número de la muestra.  

Tabla 4
Ejemplo de modelo de proyección del Estado de Resultados por el Método Marginal

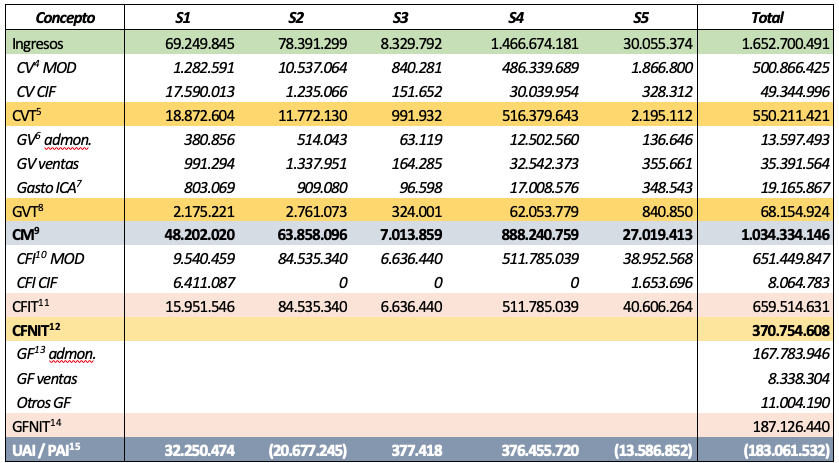
Fuente: elaboración propia

-----

Tabla 5
Funciones de Excel empleadas en los procesos estocásticos.

Fuente: elaboración propia

Paso 7 realizar el análisis de estadística descriptiva. En la Tabla 6 y en la Figura 4 se presentan algunas mediciones clásicas de estadística descriptiva y el histograma resultado de la simulación. Se puede observar que el promedio de las 2.730 corridas es negativo e igual a una pérdida $74.149.290 (COP), aunque tiene una desviación estándar con un valor cercano a la media, indicando que los datos tienden alejarse del promedio en $74.117.768 (COP).

Tabla 6
Mediciones de estadística descriptiva para la variable de salida

Fuente: elaboración propia

-----

Figura 4
Histograma de la variable de salida UAI / PAI

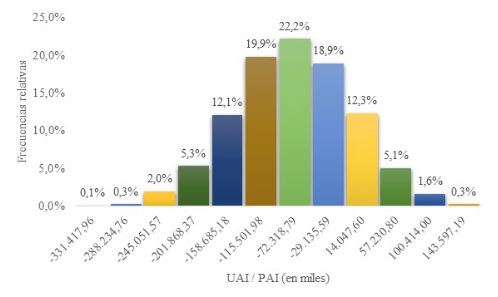
Fuente: elaboración propia

Paso 8 hacer análisis de sensibilidad. En la Figura 5 se presenta el gráfico de tornado, el cual despliega una jerarquía relativa de una variable independiente versus otras, al comparar los efectos de todas estas variables en el comportamiento de la variable dependiente. La longitud de la barra indica la cantidad de cambio que la variable independiente causa sobre los resultados o la variable dependiente, sin cambiar las demás variables de entrada. En este caso, las variables importantes de analizar son las aleatorias, que son las que presentan incertidumbre en el corto plazo, es decir, las horas de prestación del servicio por tipo de servicio.

Figura 5
Gráfico de tornados de la variable de salida

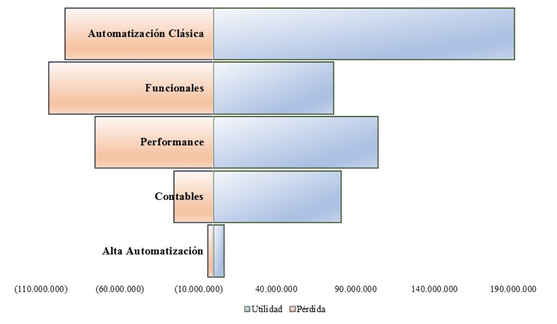
Fuente: elaboración propia

Una vez ejecutada la simulación Monte Carlo, la creación de escenarios y el análisis de la información permite gestionar el comportamiento de los gastos, costos e ingresos, para prever el de la utilidad antes de impuesto a la renta. Por ejemplo, se puede responder a preguntas cómo las siguientes:

¿Cuál es la probabilidad de que en el próximo período exista utilidad antes de impuesto? De las 2.730 corridas, 458 veces se obtiene utilidad antes de impuesto mayores a cero, por lo tanto, para esta empresa hay un 16,8% de probabilidad de que en el próximo período tenga utilidad antes de impuesto. Esto se explica que para la estructura de costos y gastos fijos que tiene, el volumen de ventas en la mayoría de los casos no es suficiente para cubrir los costos fijos, aunque todos los servicios presentan contribución marginal positiva.

El margen mínimo de utilidad antes de impuestos deseada por los inversionistas de la empresa es de un 35% ¿cuál es la probabilidad de que en el próximo período se cumplan las utilidades deseadas? Según las 2.730 corridas no hay ningún escenario que iguale o supere dicho margen de utilidad, el margen máximo fue 8,1%.

¿Cuáles son las variables que más inciden en la generación de los resultados esperados? Según el gráfico de tornados (Figura 5) de las 5 variables de entrada aleatorias, la variable del tiempo de prestación del servicio automatización clásica es la más sensible a la utilidad antes de impuesto, es decir, un cambio en el número de horas vendidas de este servicio afecta más a la utilidad que el cambio en otro tipo de servicio. En su orden, las variables más sensibles que siguen son los servicios de testing funcionales y performance.

De acuerdo a los resultados de la simulación, ¿cuál es el VaR al 95% de confianza calculadas sobre las utilidades netas en un mes? El VaR es una medida de riesgo para estimar la máxima pérdida que en un periodo de tiempo determinado la empresa puede esperar que ocurra. La información sobre la cual se ha basado el modelo tiene una periodicidad mensual, por lo tanto, este sería el horizonte de tiempo al cual se analiza el VaR. En el contexto de los resultados de la organización, el VaR se conoce como EaR -Utilidad en Riesgo, (Medina & Restrepo, 2013), en este caso, los resultados de la simulación arrojan un EaR de 119.799.248, esto quiere decir, que en un mes la empresa puede perder máximo 119 millones de pesos, con un 95% de confianza en la estimación.

Para tratar de disminuir el riesgo, con la SMC la empresa objeto de estudio también puede realizar análisis de escenarios cómo el tema clásico del escenario pesimista, el probable y el optimista. En la siguiente tabla se presenta un ejemplo del anterior esquema de escenarios:

Tabla 7
Análisis de escenarios

Fuente: elaboración propia

En la tabla anterior, se plantean el resultado mínimo de la UAI que sería el mínimo valor cercano a la cola izquierda de la distribución normal. El más probable, se ubica en el valor promedio y el máximo, es el valor más cercano a la cola derecha de la distribución de los datos. El planteamiento de estos escenarios presenta diferentes expectativas acerca de los resultados de la compañía, respecto al valor de la UAI en el próximo mes.

En conclusión, la simulación Monte Carlo es una herramienta ampliamente utilizada en diferentes ámbitos de estudio. En los negocios es útil para la proyección y estimación del valor de diferentes clases de activos, los resultados financieros en condiciones de riesgo e incertidumbre y otras decisiones de asignación de recursos. En futuras investigaciones, la simulación Monte Carlo podría aplicarse a las partidas del ORI que dependen del comportamiento futuro del valor razonable, la tasa de cambio y otras variables macroeconómicas, por lo tanto, la proyección del estado de resultados integrales bajo el contexto de las IFRS no sólo tendrá en cuenta los niveles de producción y venta para la determinación de las variables estocásticas.

En cuanto a la estimación de los resultados empresariales para la proyección del estado de resultados, es necesario definir las variables que afectan el resultado neto junto con la distribución de probabilidad y sus parámetros, una vez se identifican estos aspectos, se realiza la simulación mediante aplicaciones computacionales. El simulador crea una cantidad de números aleatorios, tantos como se le indique. Estos números aleatorios se ubican entre 0 y 1. Cada uno de ellos plantea una probabilidad y un resultado vinculado a dicha probabilidad. En la medida en que se establezcan rangos en las variaciones estimadas del resultado neto, se plantean tres escenarios entre los que se puede encontrar el resultado proyectado.

De esta manera, la SMC permite ubicar el resultado normal, la mayor pérdida o ganancia esperada acorde con cada uno de los escenarios propuestos. Para la elección de una de ellos, es necesario complementar su análisis con el diagnóstico de la situación interna y externa prevista para el futuro cercano, de esta manera los resultados de la proyección Monte Carlo adquieren mayor lógica y sentido en el contexto empresarial.

Azofeifa, C. (2004). Aplicación de la simulación Monte Carlo en el cálculo del riesgo usando Excel. Tecnología en Marcha, 17(1), 97-109.

Chase, R., & Jacobs, R. (2014). Administración de operaciones: producción y cadena de suministros. México: McGraw-Hill.

Cruz, F. (Abril - Junio de 2012). Procesos estocásticos en la valuación de proyectos de inversión, opciones reales, árboles binomiales, simulación bootstrap y simulación Monte Carlo: flexibilidad en la toma de decisiones. Contaduría y Administración, 57(2), 83-112.

Cuervo, J., Osorio, J., & Duque, M. (2013). Costeo basado en actividades ABC gestión basada en actividades ABM (Segunda ed.). Bogotá: Ecoe Ediciones.

Duque, M., Muñoz, L., & Osorio, J. (2011). El estado del costo de producción y venta y el estado de resultados en las normas internacionales de información financiera NIIF/IFRS. Contaduría Universidad de Antioquia(58-59), 13-28.

Flórez, L., & Moscoso, J. (2009). Metodología para la medición del valor en riesgo corporativo en las empresas colombianas. Contaduría Universidad de Antioquia(55), 203-221.

Gutiérrez, H., & de la Vara, R. (2008). Análisis y diseño de experimentos. México: McGraw-Hill Interamericana.

Hansen, D., & Mowen, M. (2007). Administración de costos: contabilidad y control (Quinta ed.). México, D.F.: Cengage Learning Editores S.A.

Horngren, C., Datar, S., & Foster, G. (2007). Contabilidad de costos un enfoque gerencial. México: Pearson Education.

IFRS Foundation. (2015). NIIF parte A, el marco conceptual y los requerimientos. Londres: IFRS Foundation.

Jorion, P. (2006). Value at risk: the new benchmark for managing financial risk (Tercera ed.). New York: McGraw-Hill.

Laporta, R. (2014). Manual de costos y gestión. Montevideo: Grupo Magro.

Lledó, P., & Rivarola, G. (2007). Gestión de proyectos (Primera ed.). Buenos Aires: Prentice Hall - Pearson Educación.

Mancilla H., A. (1999). Simulación: Herramienta para el estudio de sistemas reales. Ingeniería & Desarrollo, 6, 104-112.

Medina, S., & Restrepo, J. (Enero - junio de 2013). Estimación de la utilidad en riesgo de una empresa de transmisión de energía eléctrica considerando variables económicas. Cuadernos de Economía, 32(59), 103-137.

Molina, P. (Octubre de 2011). Repositorio Institucional de la Universidad de las Fuerzas Armadas ESPE. Recuperado el 23 de Enero de 2017, de Valoración financiera utilizando opciones reales y el método de simulación Montecarlo: una metodología indispensable para escenarios de incertidumbre.: http://repositorio.espe.edu.ec/bitstream/21000/4717/1/T-ESPE-032842%20-MED.pdf

Newbold, P., Carlson, W., & Thorne, B. (2013). Estadística para administración y economía (Octava ed.). Madrid: Pearson Educación.

Osorio, J., Alzate, W., & Agudelo, D. (27 de Junio de 2016). Análisis de tendencia gráfica: complemento para separar los costos semivariables en sus componentes fijo y variable. Ponencia del X Congreso Iberoamericano de Contabilidad de Gestión. Valencia, España.

Polimeni, R., Fabozzi, F., Adelberg, & Arthur. (1994). Contabilidad de costos conceptos y aplicaciones para la toma de decisiones gerenciales (Tercera ed.). Bogotá: McGraw-Hill Interamericana.

Rodriguez, L. (Marzo de 2011). Métodos Cuantitativos de Organización Industrial. Obtenido de Simulación, Método Monte Carlo: https://www.uclm.es/profesorado/licesio/Docencia/mcoi/Tema4_guion.pdf

Vanalle, R., Lucato, W., Vieira, M., & Sato, I. (2012). Uso de la Simulación Monte Carlo para la toma de decisiones en una línea de montaje de una fábrica. Información Tecnológica, 23(4), 33-44. doi:10.4067/S0718-07642012000400005

Velásquez, S., & Velásquez, R. (Septiembre de 2012). Modelado con variables aleatorias en simulink utilizando simulación montercarlo. Universidad, Ciencia y Tecnología, 16(64), 203-211.

Vélez, I. (2003). Research Gate. Recuperado el 30 de Abril de 2016, de Análisis de inversiones bajo riesgo: simulación: https://www.researchgate.net/publication/228145854_Analisis_De_Inversiones_Bajo_Riesgo_Simulacion_Including_the_Risk_in_the_Analysis_Montecarlo_Simulation

Vergara Schmalbach, J. C. (2005). Aplicación de la simulación montecarlo en la planeación financiera. Revista Panorama Económico, 13, 124-130.

Wiedeman, A., Hager, P., & Roehrl, A. (2003). Risk Net. Recuperado el 15 de Abril de 2016, de Integrated Risk Management with Cash-Flow-at Risk: https://www.risknet.de/fileadmin/eLibrary/Wiedemann-Cash-Flow-at-Risk.pdf

1. Artículo de reflexión derivado de los trabajos del Grupo de Investigación y Consultoría en Ciencias Contables – GICCO de la Universidad de Antioquia. La primera versión de este trabajo fue sustentada en el XV Congreso Internacional de Costos, Lyon – Francia

2. Docente del Departamento de Ciencias Contables. Universidad de Antioquia. Contadora Pública y Magíster en Finanzas de la Universidad de Antioquia. janeth.salazar@udea.edu.co

3. Docente del Departamento de Ciencias Contables. Universidad de Antioquia. Contador Público de la Universidad de Antioquia y Magíster en Ingeniería Administrativa de la Universidad Nacional de Colombia. wilmar.alzate@udea.edu.co