

Vol. 39 (Number 24) Year 2018 • Page 16
Irina N. POPOVA 1; Andrey I. VLASOV 2; Natalya I. NIKITINA 3
Received: 30/01/2018 • Approved: 15/02/2018
ABSTRACT: The paper studies the methods for solving the problem of optimizing logistics for the distribution of reserves in industrial enterprises. The analysis of the known basic models led to the conclusion on their limited prognostic potential, which does not allow considering the business cycles and different types of stocks by the shelf life. This paper investigates the reasons for low efficiency of the basic models of warehouse logistics. In solving this problem, the authors propose a modified approach with the calculation of the order size for the formation of reserves at the optimum level of compliance with the production needs. The terms have been identified for application of the model with the cost of order, depending on the batch size. The approach was approbated via simulation modeling for different groups of reserves by functional criteria among enterprises of one industry. The model of the fair value of production reserves was chosen as the resultant model. The results of approbation testify to the adequacy of the model with a high reliability of evaluation. |
RESUMEN: El documento estudia los métodos para resolver el problema de optimizar la logística para la distribución de reservas en empresas industriales. El análisis de los modelos básicos conocidos llevó a la conclusión sobre su potencial pronóstico limitado, lo que no permite considerar los ciclos económicos y los diferentes tipos de existencias por la vida útil. Este documento investiga las razones de la baja eficiencia de los modelos básicos de logística de almacén. Para resolver este problema, los autores proponen un enfoque modificado con el cálculo del tamaño del pedido para la formación de reservas en el nivel óptimo de cumplimiento de las necesidades de producción. Los términos han sido identificados para la aplicación del modelo con el costo de pedido, dependiendo del tamaño del lote. El enfoque fue aprobado a través de modelos de simulación para diferentes grupos de reservas por criterios funcionales entre las empresas de una industria. El modelo del valor razonable de las reservas de producción se eligió como el modelo resultante. Los resultados de la aprobación atestiguan la idoneidad del modelo con una alta fiabilidad de la evaluación. |
Companies, taking into account their resource potential, rely on the possibility of planning sustainable development. One of the most effective tools for managing the movement of material, financial, information and other resources in production and turnover is logistics (Katotkov, 2005). Logistics is a costly part of an enterprise’s business processes. In general, logistics costs are caused by the movement of material flows. Logistic processes of an enterprise have a comprehensive structure, a non-linear relationship and are influenced by many factors. For their description, a large number of parameters and a large array of information are required.
The basis of successful operation of any enterprise is the solution of the problem of minimizing costs in inventory management and at the same time maintaining the rhythm of production without stopping. Finding a balance between these two contradictions is the main goal of optimal inventory management.
Among industrial enterprises, only a few have a well-developed logistics strategy that provides for integrated management of material flows, taking into account modern life-cycle concepts (Kuzmin, 2017). In the modeling of logistics strategies, such criteria as the reduction of total costs (Ivanov et al., 2017; Nechaeva et al., 2016), differentiation of logistics services (Burinskas, & Burinskiene, 2016; Scarsi, & Spinelli, 2017; Ivanova, 2017), innovation (Klapalová, 2013) and others are used. The literature review points to a wide variety of forms and conditions regarding the level of logistic management, which does not allow one to unambiguously interpret the types of logistic strategies.
As a result, a whole complex of mathematical problems arises, the solution of which allows creating a stable logistic system (Lubentsova, 2008). Consequently, the construction of mathematical models of inventory management with a high degree of adequacy is an actual problem when creating an effective logistics system. Nevertheless, some theoretical and practical aspects are still poorly studied.
A common stock management approach is the Wilson model (Wilson, 1934) (it is also called a deterministic model for a system with a fixed order size). This model describes the process of inventory management and is characterized by the following assumptions: the intensity of the use of reserves is a priori known and constant; the delivery time is constant and known; costs do not depend on the size of the order; the absence of stocks is unacceptable. The peculiarity of this model is that the change in the level of stocks is cyclical and all the cycles of change in stocks are the same, and the maximum number of products in stock coincides with the size of the order Q. However, in practice, the demand size can almost never be specified accurately; most often, it is described in probabilistic quantities over a range interval. According to Sterligova, "it can be stated that the instrumentation in question (including all modifications of the Wilson formula) has a negative reputation among specialists. It is considered purely theoretical, unacceptable for practice; and the result of the calculation has a significant deviation from the accepted batches of orders" (Sterligova, 2005).
Based on the Wilson model, a set of inventory management models was created for various options of the functioning of logistical processes. For example, the model taking into account the change in supply costs, the model taking into account the uneven execution time of the order and the demand for the material (Solyanik, 2006), the model with VAT (Sterligova, & Semenova, 2005), etc. It seems that a deeper study of the problem is possible only if the models are classified by the complexity of their application and qualitatively new conditions in designing for different periods (Tektov, 2003).
To solve this problem, a number of researchers propose modified models. These complexities of operational inventory management are solved in the model <Q, r> – a model taking into account the requirements unmet, characterized by the following assumptions: the cost of a unit of inventory does not depend on the batch size; in the system there is not more than one uncompleted order; costs do not depend on Qi of the order level r. Unlike deterministic models, in this model, during each cycle, the system may not retain the accuracy of the order time and the cycle itself is now random (with the fictitious reserve level varying from r to r + Q).
Figure 2
Model <Q, r> of operational inventory management
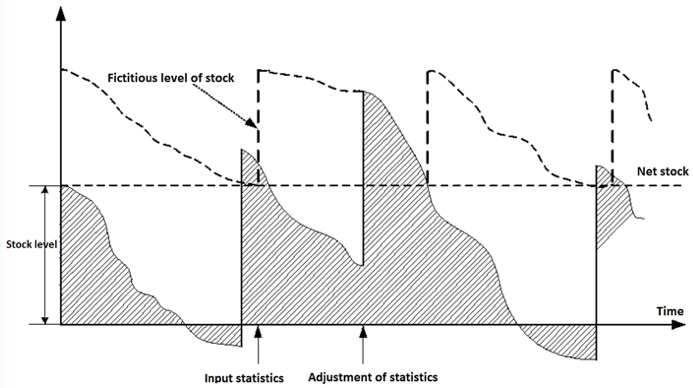
The main problem arising when applying this model is that the state of the system at any time is unknown. The moments when requirements arise (or the size of the requirements) are random. Therefore, in order to monitor the system at any time, all operations and transactions (requirements, filing orders, receipt of goods) must be immediately registered, which is often impossible in practice.
Taking into account the mentioned shortcomings, the models considered above have a low prognostic potential. They cannot be applied to manufacturing using products that have a limited shelf life, or when it is not possible to determine the exact value of demand for raw materials and to fix the state of the system at any given time. To solve this, it is necessary to identify and eliminate the reasons for the weak adequacy of mathematical models of inventory management.
Increasing the efficiency of optimal inventory management occurs due to the use of a dynamic model that takes into account the costs on organizing and servicing stocks. Let us construct a mathematical model for the next task of optimizing the inventory management scheme.

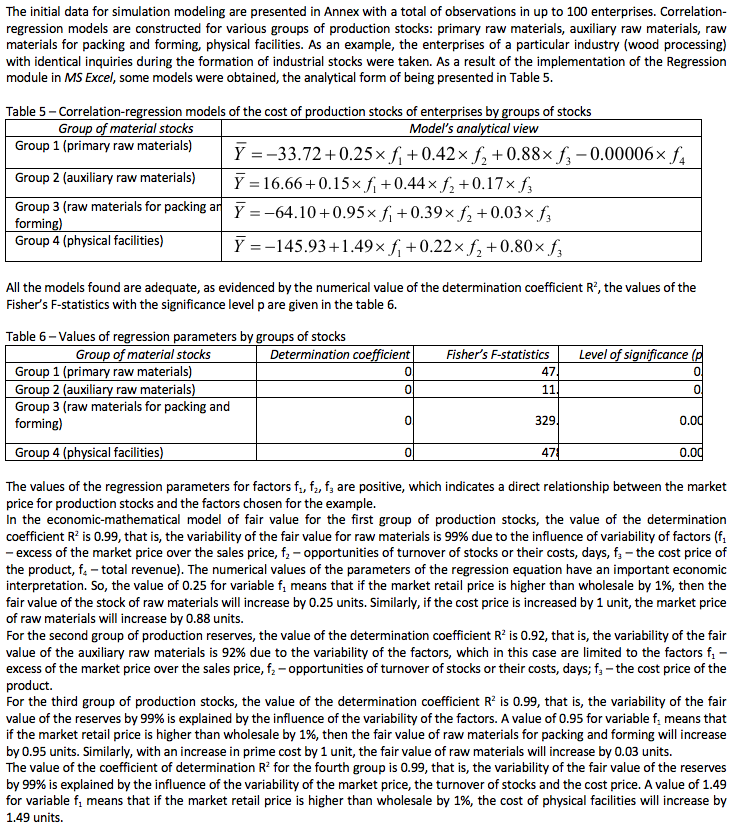
The urgency and insufficient knowledge of the problems of accounting for the interaction of the main flowing processes in industrial enterprises determined the need for scientific developments in optimizing the logistics function. In this paper, some problems of low adequacy of models are considered. The result of the study was the modified model, in which the optimal size of demand was determined during the formation of stocks. To solve the problem of managing production reserves, a methodical approach was suggested that makes it possible to determine in a timely manner the normative level of industrial reserves via: Model 1 (M1) – realizing the principle of calculating the initial (historical) cost of production reserves; Model 2 (M2) – providing an estimate of production stocks as of the reporting date; Model 3 (M3) – designed to establish the fair value of inventories. The comparative analysis of the results in simulation showed the similarity of the correlation-regression function with a high level of reliability with respect to various types of reserves.
Burinskas, A., & Burinskiene, A. (2016). A Model of Logistics Services with Heterogeneous Firms. In 13th International Conference on Industrial Logistics, ICIL 2016 – Conference Proceedings (pp. 381-388). University of Zagreb.
Groysberg, L.B., & Nesteruk, A.K. (1995). An Accelerated Probabilistic Simulation Algorithm for Estimating the Reliability of Complex Systems. Automation and Remote Control, 56(4), 602-610.
Ingber, L. (1993). Simulated Annealing: Practice versus theory. Mathematical and Computer Modelling, 18(11), 29-57.
Ivanov, D., Pavlov, A., Pavlov, D., & Sokolov, B. (2017). Minimization of Disruption-Related Return Flows in the Supply Chain. International Journal of Production Economics, 183, 503-513.
Ivanova, A.V. (2017). Logistics Service in Inventory Management. Logistics and Supply Chain Management, 2(79). 65-81.
Katotkov, V.M. (2005). Issues of Methodology of Logistics of Interacting Stream Processes. Proceedings of the Chelyabinsk Scientific Center of the Ural Branch of the Russian Academy of Sciences, 3, 105-110.
Kirkpatrick, S., Gelatt Jr., C.D., & Vecchi, M.P. (1983). Optimization by Simulated Annealing. Science, 220, 671-680.
Klapalová, A. (2013). Reverse Logistics Policy – Differences between Conservative and Innovative Reverse Logistics Management. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis, 61(7), 2285-2294.
Kuzmin, E.A. (2017). Risk and Uncertainty in Concept of Corporate Lifecycle. Problems and Perspectives in Management, 15(1), 107-114.
Lubentsova, V.S. (2008). Mathematical Models and Methods in Logistics. Samara: Samara State Technical University.
Nechaeva, P.A., Andrianova, N.V., & Sadriev, D.S. (2016). Transaction Costs in the Interaction of Logistics and Marketing in the Procurement. Academy of Strategic Management Journal, 15(1), 59-66.
Scarsi, R., & Spinelli, R. (2017). An Analysis of Strategic Groups in the Third-Party Logistics Industry. International Journal of Logistics Systems and Management, 27(4), 466-486.
Sergienko, I.V., Lebedeva, T.T., & Roshchin, V.A. (1980). Approximate Methods for Solving Discrete Optimization Problems. Kiev: Naukova Dumka. (p. 276).
Solyanik, L.G. (2006). Optimization of Inventory Management Parameters in an Industrial Enterprise. The Economic Messenger of the NMU, 1, 16-24.
Sterligova, A.N. (2005). On the Detrimental Practicality of the Wilson Formula. Logistics & System, 4, 5, 42-52, 56-61.
Sterligova, A.N., & Semenova, I. (2005). Optimal Order Size or Wilson's Mysterious Formula. Logistics & System, 2, 64-69.
Tektov, D.A. (2003). Dynamic and Statistical Models of Inventory Management in Retail Trade (Ph.D. Thesis). St. Petersburg: St. Petersburg State Polytechnic University. (p. 159).
Wilson, R.H. (1934). A Scientific Routine for Stock Control. Harvard Business Review, 13, 116-128.
Table 1
Data for the simulation model of regression by stocks of Group 1 (primary raw materials)
Observations |
Market price, units |
Influence factors |
|||
f1 |
f2 |
f3 |
f4 |
||
Enterprise 1 |
10 |
103.3 |
24.0 |
8.5 |
27,174 |
Enterprise 2 |
8 |
100.6 |
18.0 |
9.5 |
76,432 |
Enterprise 3 |
9.5 |
102.9 |
22.0 |
9 |
14,231 |
Enterprise 4 |
10 |
103.0 |
23.0 |
8.5 |
71,843 |
<…> |
<…> |
<…> |
<…> |
<…> |
<…> |
Enterprise 98 |
8 |
100.8 |
19.0 |
9 |
42,312 |
Enterprise 99 |
9.5 |
102.4 |
21.0 |
9.5 |
12,920 |
Enterprise 100 |
8.5 |
102.2 |
20.0 |
9 |
16,976 |
Table 2
Data for the simulation model of regression by stocks of Group 2 (auxiliary raw materials)
Observations |
Market price, units |
Influence factors |
||
f1 |
f2 |
f3 |
||
Enterprise 1 |
52 |
103.3 |
24 |
51 |
Enterprise 2 |
48 |
100.6 |
18 |
49 |
Enterprise 3 |
50 |
102.9 |
22 |
49 |
Enterprise 4 |
51 |
103 |
23 |
50 |
<…> |
<…> |
<…> |
<…> |
<…> |
Enterprise 98 |
49 |
100.8 |
19 |
48 |
Enterprise 99 |
50 |
102.4 |
21 |
49 |
Enterprise 100 |
50 |
102.2 |
20 |
49 |
-----
Table 3
Data for the simulation model of regression by stocks of Group 3 (raw materials for packing and forming)
Observations |
Market price, units |
Influence factors |
||
f1 |
f2 |
f3 |
||
Enterprise 1 |
45 |
103.3 |
24 |
44 |
Enterprise 2 |
40 |
100.6 |
18 |
40 |
Enterprise 3 |
44 |
102.9 |
22 |
42 |
Enterprise 4 |
44.5 |
103 |
23 |
41 |
<…> |
<…> |
<…> |
<…> |
<…> |
Enterprise 98 |
41 |
100.8 |
19 |
50 |
Enterprise 99 |
43 |
102.4 |
21 |
44 |
Enterprise 100 |
42.5 |
102.2 |
20 |
45 |
-----
Table 4
Data for the simulation model of regression by stocks of Group 4 (physical facilities)
Observations |
Market price, units |
Influence factors |
||
f1 |
f2 |
f3 |
||
Enterprise 1 |
60 |
103.3 |
24 |
59 |
Enterprise 2 |
38 |
100.6 |
18 |
38 |
Enterprise 3 |
52 |
102.9 |
22 |
50 |
Enterprise 4 |
58 |
103 |
23 |
56 |
<…> |
<…> |
<…> |
<…> |
<…> |
Enterprise 98 |
40 |
100.8 |
19 |
39 |
Enterprise 99 |
50 |
102.4 |
21 |
48 |
Enterprise 100 |
42 |
102.2 |
20 |
39 |
1. Cand. Sc. in Economics, Assistant professor, Ural State University of Economics (62, 8 Marta Str., Ekaterinburg, 620144, Russian Federation). Contact e-mail: ipopova@k66.ru
2. Cand. Sci. in Engineering, Assistant professor, Bauman Moscow State Technical University, Russian Federation (ul. Baumanskaya 2-ya, 5, Moscow, 105005, Russian Federation). Contact e-mail: vlasov@iu4.ru
3. Dr. Sc. in Education, Professor, Russian State Social University (4/1, Vil'gel'ma Pika Str., Moscow, 129226, Russian Federation). Contact e-mail: nn0803@mail.ru