

Vol. 38 (Nº 53) Año 2017. Pág. 23
Germán HERRERA-VIDAL 1; Heiner MARRUGO-CERMEÑO 2
Recibido: 03/07/2017 • Aprobado: 30/07/2017
RESUMEN: En este trabajo se desarrolla un modelo de programación lineal fundamentado en la optimización binivel aplicado en la planificación en la gestión de las operaciones de la cadena de aprovisionamiento, el cual contempla la maximización de la utilidad de la empresa caso estudio. Dado que en los mercados globales la competencia de las empresas no es entre sus productos sino entre sus cadenas de suministro, quienes tengan mayores eficiencias estarán en mejores condiciones de competir, y para encontrar dicho logro se hace necesario la utilización de técnicas cuantitativas que permitan tomar las mejores decisiones al solucionar un problema. Primeramente se hizo una caracterización de la cadena, luego se estructuró un modelo de referencia conceptual, consiguiente a esto se hizo la formulación matemática y por último la determinación de la solución y validación de los resultados. Los hallazgos encontrados evidencian un ambiente favorable si se toman las decisiones de una forma coordinada entre los agentes, logrando así administrar eficientemente la cadena de suministro del caso de estudio, beneficiar la rentabilidad de los inversionistas y la satisfacción de los clientes. |
ABSTRACT: In this work a linear programming model is developed based on binary optimization applied in the planning of the operations of the supply chain, which contemplates the maximization of the utility of the company case study. Given that in global markets the competition of the companies is not between their products but between their supply chains, those that are greater efficiencies will be in better conditions of competition, and to find that achievement requires the use of quantitative techniques that allow Take The best decisions when solving a problem Firstly a feature of the chain was made, then a conceptual reference model was structured, a single time was made the mathematical formulation and finally the determination of the solution and the validation of the results. The findings show a favorable environment if the decisions are made in a coordinated way among the agents, thus managing efficiently the supply chain of the case study, benefiting the profitability of the investors and the satisfaction of the clients. |
El entorno globalizado en el cual están inmersa las organizaciones actualmente ha traído consigo una mayor competitividad tanto locales, nacionales e internacionales que tratan de captar cada vez más una porción de un mercado cada día más exigente y expectante. Hoy por hoy las empresas trabajan en la organización estratégica de las áreas que la conforman y así mismo en la integración de los procesos, con el fin de mejorar la productividad y calidad en los productos y servicios que ofertan. El uso de nuevas técnicas, filosofías, la implantación de nuevas tecnologías, se traducen en brindarle un mejor producto o servicio al cliente. Estos factores influyen en que las organizaciones integren todas las áreas que la conforman con el fin de hacer un bueno uso de los recursos organizacionales. Hoy en día, los modelos de negocios del mundo moderno están en continuo desarrollo, entrando en nuevas tendencias y economías, nuevas áreas industriales y hasta nuevos modelos en un entorno de alta competitividad (Herrera, 2014).
De acuerdo con Sana, Herrera & Acevedo (2017), la cadena de suministro puede ser entendida como un conjunto de empresas compuestas por proveedores, fabricantes, distribuidores y clientes, conectadas entre sí por una serie de actividades como planificación, coordinación y control y una serie de flujos como el de materiales, información, contratos y dinero. Buscando siempre la integración y la colaboración con el fin de tener una visión completa de lo que ocurre en la cadena. Existen varias formas de planear las decisiones en la cadena de suministro y que están relacionadas con la planeación de la estrategia de operaciones, la administración de la demanda, la planeación y programación de la producción, los esquemas de contratación y mecanismos de distribución. La planificación conjunta es usada para alinear a los miembros y coordinar las decisiones en cuanto al aprovisionamiento, inventarios, colocación y entrega de las ordenes (Cao et al., 2010), y se basa en el hecho de que los socios colaboradores deben trabajar juntos para resolver los problemas de la cadena de suministro (Kumar, 2001; Min et al., 2005).
El concepto de planificación se puede aplicar tanto al proceso de planificación de la distribución de los productos hacia los clientes, como en el proceso de planificación de aprovisionamiento de los proveedores (Beamon, 1998). En este sentido, Stadtler (2005) establece que los procesos de planificación se pueden aplicar a los procesos de planificación que interactúan con los clientes y aquellos que actúan con los proveedores. En este sentido, Berning et al., (2004) consideran que la planificación, ayuda a las empresas inmersas en un contexto de cadena de suministro, a trabajar de forma simultánea apoyando la transparencia de los procesos, la mayor flexibilidad y la reducción de los tiempos de respuesta.
Existen diferentes tipos de modelos de gestión para las cadenas de suministros, dentro de estos se encuentran los modelos conceptuales y los modelos analíticos, los modelos conceptuales consisten en herramientas descriptivas, que subrayan los aspectos principales y las variables relevantes implicadas en un problema de planificación, y los modelos analíticos ayudan a la toma de decisiones desde un entorno cuantitativo basados en diferentes técnicas de la investigación operativa, entre ellas cabe destacar la programación matemática, teoría de inventarios, teoría de la decisión, procesos de Markov y procesos jerárquicos, entre otros (Lario & Pérez, 2005). Es por esto que programación lineal se convierte en una técnica de gran utilidad para el proceso de toma de decisiones. De acuerdo con Alvarado (2011) la importancia de la aplicación de la programación lineal radica en la fortaleza de modelar problemas complejos y la posibilidad que tienen los usuarios para resolver modelos de gran escala mediante programas de cómputo sustentados en el procedimiento de resolución simplex. Sin embargo, lo más importante es el análisis pos óptimo, el cual nos permite realizar cambios en el modelo original con el fin de encontrar un valor óptimo aún mejor o conocer los resultados que se darían si se cambia el plan de producción antes de ejecutar el proyecto representado en el modelo.
La planificación y optimización de la cadena permite competir con éxito en los mercados actuales, gracias al resultado que produce la conjunción de los objetivos de la logística y la implantación de mejores prácticas en la planificación de compras y la proyección de la demanda, producción, transporte, almacenaje, inventarios y servicio al cliente. Es por esto que el éxito de una organización que reduce costos y que satisface las necesidades de sus clientes, depende de una cadena de suministros bien gestionada, integrada y flexible que sea controlada en tiempo real y en la que fluya información eficientemente entre los distintos niveles de la misma. Para este caso se tomó de referencia la cadena de aprovisionamiento de una empresa del sector plástico de la ciudad de Cartagena – Colombia, cuyo objetivo es la producción y comercialización de envases, tapas y piezas plásticas, con tecnologías de inyección, soplado, extrusión-soplado e inyección-soplado. La necesidad de realizar esta investigación surge con el fin de diseñar una adecuada planificación en la cadena de aprovisionamiento, que pueda lograr una mejor adquisición de la materia prima y materiales, con el fin de mantener un normal desarrollo en la fabricación de los productos y por ende lograr tiempos de entrega oportunos.
Un diagnóstico inicial mediante herramientas de evaluación rápida de planta planteado por Goodson (2002) y del modelo referencial en logística propuesto por Feres (2014) logró evidenciar que dentro de la cadena de aprovisionamiento del caso estudio, existe una inadecuada planificación de materiales con respecto a los proveedores, ausencia de indicadores que reflejan la competitividad del sistema logístico, y asimismo, bajos niveles de tecnologías de información que imposibilita que la red esté conectada por intermedio de un sistema de información y de comunicación estándar. Dado lo anterior se brindan instancias habilitadoras para poder llevar a cabo el diseño de un modelo de programación lineal para la planificación en la gestión de las operaciones de la cadena de aprovisionamiento, que permitan poder establecer estrategias a la hora de tomar decisiones, con el fin de maximizar las utilidades e incrementar la competitividad tanto de la empresa como de los agentes proveedores que intervienen en la cadena. Para el desarrollo de este trabajo, se elabora una primera parte relacionada con la metodología, luego, se construye la modelación matemática, a partir de esto se hacen un análisis y discusión de los resultados, y consiguiente las conclusiones.
Los problemas de planificación en la cadena de suministros requieren de la toma de decisiones de los diferentes agentes que la componen, y en la mayoría de los casos cada uno busca su propio beneficio y para conseguirlo pueden llegar a afectar negativamente los intereses de los demás actores a lo largo de los niveles de la cadena de suministro (Sana, Herrera & Acevedo, 2017). Las decisiones multinivel son consideradas como una herramienta importante en todo proceso de planeación en donde hay la presencia de más de un actor. En el marco del modelado matemático, Calvete et al., (2010) plantearon que la programación multinivel generaliza para el tratamiento de los sistemas jerárquicos, la programación matemática estándar. Los sistemas modelados a través de esta herramienta, están caracterizados por la existencia de distintos niveles de decisión con una jerarquía establecida entre ellos, de manera que cada nivel tiene un objetivo, controla sólo algunas de las variables y sus decisiones se ven afectadas por las tomadas en los niveles superiores. Así, el primer decisor elige los valores para las variables que controla para minimizan (maximizar) su función objetivo, estos valores condicionan parcialmente el valor de la función objetivo del segundo decisor y pueden restringir los valores que éste puede elegir para las variables que controla.
Para Greenberg (2015), la programación binivel es un caso particular de la programación multinivel, un enfoque de optimización en el que las variables de decisión pueden separarse en grupos (llamados “niveles”) que representan subsistemas independientes, o casi independientes en el problema original, con el fin de explotar algunos principios de descomposición que faciliten los algoritmos de solución. Por ejemplo, cuando en un programa lineal la matriz de restricciones tiene una forma particularmente dócil de tratar o cuando un subconjunto de variables (niveles) está obligado a ser la solución de un problema de optimización de un subproblema del planteamiento original, las variables que participan en la función objetivo principal son llamadas “del nivel superior” y representan las posibles acciones del líder que toma decisiones, mientras que el resto de las variables de decisión están en “el nivel inferior” y equivalen a las acciones que pueden tomar los seguidores del líder en las interacciones.
Un problema de programación binivel (BPL) se refiere a problemas de optimización jerárquica conformado por un líder, que se ven limitados por otro problema de optimización conformado por un seguidor. Se utiliza a menudo para describir situaciones en las que varios agentes, interconectados en una estructura jerárquica, con objetivos independientes, buscan la solución a problemas que se encuentran relacionados entre sí como es el caso en donde el líder establece parámetros que influyen en el seguidor o viceversa. (Sana, Herrera & Acevedo, 2017). Cada grupo puede ser un individuo o un organismo que tiene objetivos independientes, quizás mutuamente contradictorios (Bard, 2013). De acuerdo con Guzmán, et al., (2008) se consideran dos niveles de decisión, donde el nivel superior esta conformado por un líder, quien controla un vector de decisión y el nivel inferior, conformado por los seguidores, quienes controlan el otro vector.
El líder y el seguidor juegan “el juego de duopolio”, donde el líder escoge el vector de decisión que maximice su utilidad o que minimice sus costos, y el seguidor teniendo en cuenta la decisión del líder, escoge su vector de decisión que de igual busque le mismo objetivo. Dado lo anterior el problema se formula de la siguiente manera:

Para la solución del problema se asume que el nivel alto primero específica X1 y el nivel bajo especificara X2 teniendo total conocimiento de la decisión del nivel alto (Guzmán et al., 2008). En este caso se plantea una cadena de aprovisionamiento, en la que intervienen la empresa caso de estudio, proveedores y clientes, y se busca maximizar la utilidad de la empresa a la vez que se maximicen las utilidades de los proveedores, que son los que abastecen la materia prima. Donde el nivel superior está conformado por la empresa y el nivel inferior por los proveedores.
Para la construcción del modelo conceptual del problema objeto de estudio, se tuvieron en cuenta dentro de la cadena de suministros los agentes participantes, cada uno asociados a un determinado conjunto, de igual forma todos los elementos que relacionan a cada uno de los agentes, como es el caso de las materias primas y los productos. En la figura 1. Se registra en detalle el modelo conceptual planteado.
Figura 1. Representación gráfica del modelo conceptual
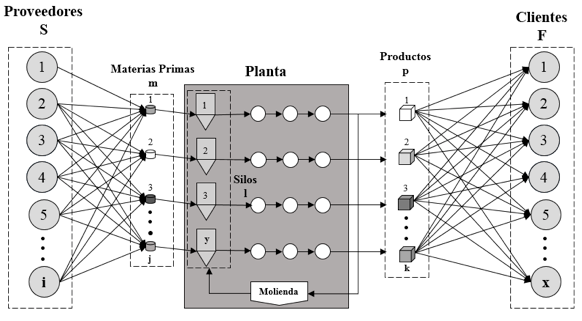
En la cadena de abastecimiento del caso de estudio intervienen “i” proveedores, una planta conformada por “y” silos de almacenamientos, a los cuales llegan “j” materias primas, para poder ser transformadas y producir “k” productos, que van a ser distribuidos a “x” clientes. A partir de esto se declaran cada uno de los conjuntos necesarios para la construcción del modelo, teniendo en cuenta los agentes que intervienen, la configuración del sistema y los flujos de materias primas y productos que se presentan.
s Proveedores (s: 1,2,3….i)
m Materia prima (m: 1,2,3….j)
p Productos (p: 1,2,3….k)
f Clientes (f: 1,2,3….x)
l Silos de Abastecimiento (l: 1,2,3….y)
r Reciclado (r: 1,2,3….w)
Se describen los parámetros del modelo propuesto, los cuales están ligados con los costos de producción, costo de transporte, costo de inventario, costo manipulación, costo de compra, precios de los productos y de las materias primas, limitaciones de capacidad y demanda requerida por los clientes.
PVSP(s,m) Precio de venta del proveedor "s" de la materia prima "m" en Kgs
UMP(m,p) Unidad de materia prima "m" para la elaboración del producto "p" en Kgs
CTSP(s,m) Costo unitario de transporte desde el proveedor "s" hacia la planta de la materia prima "m"
CMI(s,m) Costo unitario de manipulación de inventario desde el proveedor "s" hacia la planta de la materia prima "m" en Kgs
CAPS(s,m) Capacidad del proveedor "s" de la materia prima "m"
PVPC(p) Precio de venta del producto "p" desde la planta hacia el cliente
CUCOM(s,m) Precio unitario de compra desde el proveedor "s" de materia prima "m"
CUPROD(p) Costo unitario de producción del producto "p"
CUALMP(p) Costo unitario de producción del producto "p"
CUTPC (p,f) Costo unitario de transporte del producto "p" hacia el cliente "f"
DEM(p,f) Demanda del producto "p" del cliente "f"
CAPP(p) Capacidad de la planta para el producto "p"
CAPL(l) Capacidad de los silos de abastecimiento "l" para la materia prima "m"
CAPALM(p) Capacidad de almacenamiento de productos "p"
PRPT(p) Porcentaje equivalente de reproceso de producto terminado de cada del producto "p"
UPT(p) Unidades en peso del producto terminado de cada producto "p"
CAPMOL(r) Capacidad de producción en molienda de reciclado "r"
INVR(r) Inventario inicial de producto reciclado "r";
CUPRM(r) Costo unitario de producción de producto reciclado "r"
CALMR(r) Costo unitario de inventario del reciclaje "r" por Kgs
UMR(m,r) Unidad de materia prima "m" con reciclado "r"en Kgs
Las variables del modelo propuesto están ligadas a las cantidades que se deben producir en la planta, los niveles de inventarios que se deben tener de cada uno de los productos, las cantidades que se deben producir por parte del proveedor, y los objetivos asociado la optimización por parte de cada uno de los agentes, proveedor y fabrica que corresponde a la maximización de las utilidades brutas. A continuación, se declaran las variables del modelo:
QPPC(p) Cantidad producida en la planta del producto "p" en unds
QPSA(s,m) Cantidad producidas por el proveedor "s" de la materia prima "m" en Kgs
QURT(r) Cantidad de unidades totales recicladas "r" en Kgs
QRALM(r) Cantidad de unidades almacenadas de "r" en Kgs
QRMP(m) Cantidad reciclada de materia prima "m" en Kgs
QURC(p) Cantidad de unidades recicladas por producto "p" en unds
QURT(r) Cantidad de unidades totales a reciclar de "r" en Kgs
DEMUP(m) Cantidad de unidades a pedir de materia prima "m" en Kgs
PROMOL(r) Cantidad Producida por la molienda de "r" en Kgs
QEPC(p,f) Cantidad entregada desde la planta hacia el cliente "f"
QALMP(p) Cantidad de unidades almacenadas del producto "p" en unds
Zp Utilidad bruta total de la planta (Nivel alto)
Zs Utilidad bruta total del proveedor (Nivel bajo)
La función objetivo de la empresa caso estudio (Nivel alto) consiste en maximizar sus utilidades brutas. La ecuación [1], muestra la formulación matemática que representa la forma de calcular las utilidades totales producto de las ventas y los costos asociados a la producción, compra, transporte, inventarios y reciclado.
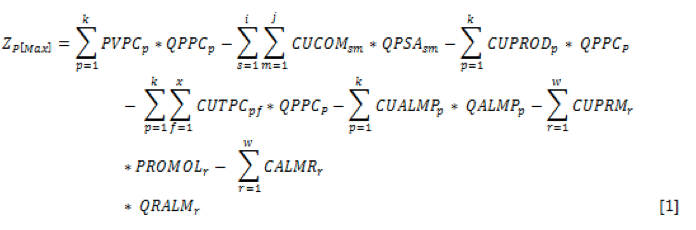
La función objetivo para los proveedores (Nivel bajo), está definida como la maximización de sus utilidades brutas. La ecuación [2], muestra la formulación matemática que representa la forma de calcular las utilidades totales producto de las ventas y los costos asociados al transporte y manipulación.
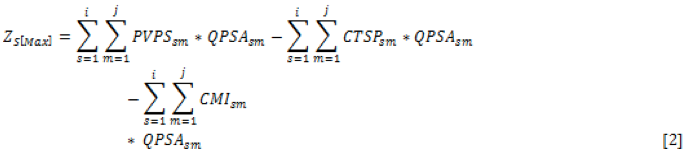
Se establecen cada una de las limitaciones del modelo, asociadas al control de cantidades, satisfacción de la demanda, capacidad, inventarios y no negatividad.

Para el desarrollo del diseño del modelo de programación binivel, se hace necesario definir el juego de duopolio de Stackelberg, declarando en esta etapa los niveles y los diferentes conjuntos que se forman en la cadena (Stackelberg, 2007), aquí también se define el actor de la cadena que hará las veces del nivel alto como es el caso de la empresa caso de estudio y quien y el actor del nivel bajo a quien se le denominará proveedores. En la tabla 1 se definen las restricciones de acuerdo variables de decisiones a considerar para ambos niveles.
Tabla 1. Restricciones para cada uno de los niveles
Agente Caso de Estudio (Nivel Alto) |
Agente Proveedores (Nivel Bajo) |
||
Restricción de Demanda |
[3] |
Restricción de Demanda |
[3] |
Restricción Equilibrio de Producción |
[4] |
Restricción Equilibrio de Producción |
[4] |
Restricción de Capacidad Planta |
[5] |
Restricción de Capacidad Planta |
[5] |
Restricción de Equilibrio de Almacenamiento |
[6] |
Restricción de Equilibrio de Almacenamiento |
[6] |
Restricción de Control de Cantidades Recibidas en Kgs desde el Proveedor |
[7] |
Restricción de Control de Cantidades Recibidas en Kgs desde el Proveedor |
[7] |
Restricción de Capacidad de Silos |
[8] |
Restricción de Capacidad de Silos |
[8] |
Restricción de Capacidad de Silos |
[9] |
Restricción de Capacidad de Silos |
[9] |
Restricción Demanda del Proveedor |
[10] |
Restricción Demanda del Proveedor |
[10] |
Restricción Capacidad Proveedor |
[11] |
Restricción Capacidad Proveedor |
[11] |
Restricción de Control de Cantidades Recicladas en Kgs por Producto |
[12] |
Restricción de Control de Cantidades Recicladas en Kgs por Producto |
[12] |
Restricción de Equilibrio de Unidades Recicladas |
[13] |
Restricción de Equilibrio de Unidades Recicladas |
[13] |
Restricción Capacidad Molienda |
[14] |
Restricciones de no negatividad |
[18-22] |
Restricción de equilibrio de inventario en el área de reciclado |
[15] |
|
|
Restricción de Cantidades Recicladas de materia prima en Kgs |
[16] |
||
Restricción de Capacidad de Almacenamiento |
[17] |
||
Restricciones de no negatividad |
[18-22] |
||
En forma general el modelo genera un total de 108 variables de decisión, de las cuales 4 corresponden a la variable QPPCp, 56 a la variable QPSAsm, 28 a la variable QEPCpf , 4 a la variable QURCp y 4 para la variable QMRPm; además presenta un total de 103 restricciones en toda la construcción del modelo involucrando ambos agentes.
El modelo se corrió en un equipo con características de 4.00 GB de memoria RAM y un sistema operativo de 32 bits con Windows 7. Para poder determinar las utilidades de cada uno de los agentes, y el resultado óptimo de las variables, se utilizó la ayuda del software GAMS (General Algebraic Modeling System), como su nombre lo indica es un lenguaje de modelización, más que un programa para resolver problemas de optimización. En este caso como el tipo de problema es no lineal se utilizó el optimizador Conopt , el cual maneja como fundamento algorítmico al gradiente reducido generalizado (GRG), la programación lineal secuencial y la programación cuadrática secuencial para determinar el valor mínimo o máximo de la función objetivo.
Para poder resolver un problema con GAMS, es necesario generar un fichero de órdenes (denominado fichero GMS) que debe contener todas las instrucciones básicas y planteamiento del modelo que se desea resolver. Una vez generado el fichero, se ejecuta GAMS y el resultado se genera de forma automática en un fichero distinto (fichero LST), (Casasus, et al., 2008). El fichero se divide en varios bloques y cada bloque representa una parte del problema. A continuación se detalla la estructura del modelo programado:
F1max.. Zp =E= SUM((p),PVPC(p)*QPPC(p)) - SUM((s,m),CUCOM(s,m)*QPSA(s,m))
- SUM((p),CUPROD(p)*QPPC(p)) - SUM((p,f),CUTPC(p,f)*QPPC(p))
- SUM((p),CUALMP(p)*QALMP(p)) - SUM((r),CUPRM(r)*PROMOL(r))
- SUM((r),CALMR(r)*QRALM(r));
F2max.. Zs =E= SUM((s,m),PVSP(s,m)*QPSA(s,m)) - SUM((s,m),CTSP(s,m)*QPSA(s,m))
- SUM((s,m),CMI(s,m)*QPSA(s,m));
R1(p,f).. QEPC(p,f) =L= DEM(p,f);
R2(p).. QPPC(p) =E= SUM((f),QEPC(p,f));
R3(p).. QPPC(p) =L= CAPP(p);
R4(p).. QALMP(p) =E= QPPC(p)-SUM((f),QEPC(p,f));
R5(m).. DEMUP(m) =E= SUM((p),UMP(m,p)*QPPC(p));
R6(m,l)$(ord(l) ne 5)..DEMUP(m) =L= CAPL(l);
R7(m,l)$(ord(l) eq 5)..QRMP(m) =L= CAPL(l);
R8(m).. SUM((s),QPSA(s,m)) =L= DEMUP(m);
R9(s,m).. QPSA(s,m) =L= CAPS(s,m);
R10(p).. QURC(p) =E= QPPC(p)*PRPT(p)*UPT(p);
R11(r).. QURT(r) =E= SUM((p),QURC(p));
R12(r).. PROMOL(r) =E= CAPMOL(r);
R13(r).. QRALM(r) =E= INVR(r)+QURT(r)-PROMOL(r);
R14(m,r).. PROMOL(r)*UMR(m,r) =E= QRMP(m);
R15(p).. QALMP(p) =L= CAPALM(p);
MODEL modeloA/F1max,R1,R2,R3,R4,R5,R6,R7,R8,R9,R10,R11,R12,R13,R14,R15/;
MODEL modeloB/F2max,R1,R2,R3,R4,R5,R6,R7,R8,R9,R10,R11/;
OPTION NLP = CONOPT;
OPTION ITERLIM=300000;
OPTION RESLIM=100000;
OPTION subsystems;
option optca=0;
option optcr=0.01;
solve modeloA using RMINLP maximizing Zp;
solve modeloB using RMINLP maximizing Zs;
Analíticamente se pudieron determinar los resultados obtenidos, donde la función objetivo cuando se lleva a cabo sin optimización binivel, la planta adquiere una utilidad bruta de 40.925,20 USD dólares y cuando se programa bajo los principios del juego de duopolio las utilidades equivalen a 58.652,44 USD dólares, representando un incremento sustancial del 43,31%. Para el caso de los proveedores las utilidades brutas en un ambiente sin optimización binivel son de 11.141,80 USD dólares y con optimización binivel de 11.464,31 USD dólares, para un incremento del 2,89%. Estos resultados fueron validados mediantes visitas a la empresa y talleres de socialización con los proveedores, donde evidentemente se reflejan beneficios en las utilidades de ambos agentes al compararlos con las utilidades normales de un periodo de tiempo determinado. Para esto se debe tener muy en cuenta las decisiones que debe tomar los agentes correspondientes, lo cual garantice una eficiente gestión en planificación de la cadena de aprovisionamiento (Ver tabla 2).
Tabla 2. Valores de las funciones objetivos de los agentes
Agentes |
Optimización sin binivel |
Optimización binivel |
Incremento |
Planta |
40.925,20 USD |
58.652,44 USD |
43,31% |
Proveedor |
11.141,80 USD |
11.464,31 USD |
2,89% |
En la tabla 3 se resume la solución óptima de la variable cantidad de productos que deben ser entregados a los diferentes clientes QEPCpf, teniendo en cuenta que es una variable de decisión fundamental para el modelo por lo que representa incidencia directa con el cliente y la meta buscada.
Tabla 3. Resultados de la variable cantidad entregada desde la planta hacia el cliente
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
|
P1 |
10.000 |
20.000 |
- |
- |
- |
- |
70.000 |
P2 |
5.000 |
15.000 |
25.000 |
35.000 |
20.000 |
- |
- |
P3 |
50.000 |
20.000 |
30.000 |
- |
- |
- |
- |
P4 |
45.000 |
15.000 |
25.000 |
- |
- |
15.000 |
- |
A su vez en la tabla 4 se detalla la solución de la variable cantidad producidas por el proveedor "s" de la materia prima "m" QPSAsm, Siendo una variable indispensable al momento de tomar las decisiones respecto al aprovisionamiento de materias primas.
Tabla 4. Cantidad producidas por el proveedor "s" de la materia prima "m"
M1 |
M2 |
M3 |
M4 |
|
S1 |
100.000 |
- |
- |
- |
S5 |
- |
100.000 |
- |
|
S6 |
- |
- |
100.000 |
- |
S11 |
- |
- |
- |
100.000 |
Con respecto a las soluciones anteriores, cabe destacar que gran parte de los problemas de planificación en la cadena de suministros requieren de la toma de decisiones de los diferentes agentes que la componen, es por esto que las decisiones que toma el agente planta del caso de estudio influye de manera directa en los resultados esperados por el agente proveedor de la cadena. Es aquí donde toma importancia el modelo propuesto de modelo de programación lineal para la planificación, dado que permite una sincronización y coordinación en la gestión de las operaciones de la cadena de abastecimiento, obteniendo así una solución al problema abordado. La validación del modelo inicialmente consistió en reflejar los resultados encontrados a través de visitas in situ, de igual forma se llevó a cabo un taller de socialización de los resultados obtenidos con los entes encargados de la parte logística y de producción de la empresa del sector plástico. Este permitió poder comparar la calidad de la respuesta del modelo, así como también proponer ideas de mejora en el proceso de gestión de operaciones, de tal forma que se minimicen los problemas logísticos que actualmente existen.
La necesidad que tienen las empresas pertenecientes a una cadena de suministro, en búsqueda de la mejor planificación de sus operaciones, es una de las principales preocupaciones en el entorno de mercado actual. Esto se debe a que existen múltiples agentes en la cadena, variedad en los niveles y amplias estructuras. Trayendo consigo inconvenientes asociados con la coordinación de los diferentes procesos que interrelacionan a los distintos actores de la cadena, principalmente la relación proveedor y fabricante.
En esta investigación se presentó una propuesta estructural de modelo conceptual, el cual permitió describir las principales característica, parámetros y variables de la cadena de aprovisionamiento del caso de estudio, logrando facilitar un mejor entendimiento a la hora de construir el modelo matemático de programación binivel con el fin de determinar las utilidades de los participantes. Para el diseño del modelo de planificación en la gestión de las operaciones de la cadena de aprovisionamiento, se hizo necesario de herramientas cuantificas y de informáticas como es el caso del software GAMS, y a partir de la metodología planteada se pudo determinar en forma óptima los valores de la función objetivo tanto del nivel alto como es el caso de empresa del sector plástico, como del nivel bajo como es el caso de los agentes proveedores, así como también de las variables de decisión del modelo, como las cantidades producidas por el proveedor y las cantidades de productos a entregar hacia los clientes.
En síntesis la optimización bi-nivel es una herramienta de aplicación muy importante para la toma de decisiones por lo que las decisiones son de tipo secuencial, jerárquicamente del nivel más alto al nivel más bajo. El nivel de decisión más bajo ejecuta sus acciones después que el nivel más alto ha tomado las suyas. Y es en esta relación directa donde la optimización bi-nivel encuentra la mejor solución para todos los participantes. Para futuras investigaciones, se deja el campo abierto para incorporar un ambiente de tipo colaborativo entre los agentes planta y proveedor, teniendo en cuenta los volúmenes de productos reciclados en todas las líneas de producción, dado la baja capacidad de la molienda. Procurando así generar mayor eficiencia en las materias primas y garantizar mejores utilidades para todos los participantes.
ALVARADO, Jorge. El Análisis Post-Optimal en Programación Lineal Aplicada a la Agricultura. Revista Reflexiones. 2011. Facultad de Ciencias Sociales. Universidad de Costa Rica, p. 161-173.
BARD, Jonathan. Practical bilevel optimization. Algorithms and applications. Springer Science & Business Media. 2013. ISBN 1475728360, 9781475728361.
BEAMON, Benita. Supply chain design and analysis: models and methods. International Journal of Production Economics. 1998. Vol. 55. No. 3. p. 281-294.
BERNING, Guido., BRANDENBURG, Marcus., GÜRSOY, Korhan., and KUSSI, Jürgen. Integrating collaborative planning and supply chain optimization for the chemical process industry methodology. Computers and Chemical Engineering. 2004. Vol. 28. No. 6. p. 913–927.
CALVETE, Herminia., and GALÉ, Carmen. A Multiobjective Bilevel Program for Production-Distribution Planning in a Supply Chain. Multiple Criteria Decision Making for Sustainable Energy and Transportation Systems. 2010. p. 155-165.
CAO, Mei., VONDEREMBSE, Mark., ZHANG, Qingyu., and RAGU-NATHAN, Ts. Supply chain Collaboration: conceptualization and instrument development. International Journal of Production Research. 2010. Vol. 48, No. 22. p. 6613-6635.
CASASUS, Trinidad., MOCHOLI, Manuel. Optimización económica con GAMS. Valencia, Departamento de Economía y Matemática. Universidad de Valencia. 2008.
FERES, Sahid. Estudio de la Caracterización de la Logística en Colombia. Servicio Nacional de Aprendizaje- SENA. 2014. Colombia.
GREENBERG, Harvey. Mathematical Programming Glossary. [En línea] 2015. [Consultado en Marzo ,2017]. https://glossary.informs.org/ver2/mpgwiki/index.php?title=Main_Page
GOODSON, Eugene. Read a plant fast. Harvard business review. 2002. p. 3-25
GUZMAN, Luceny., RAMÍREZ, Diana., YIE, Rubén., ACERO, Karen. UCRÓS, Martha., and PATERNINA, Carlos. Modelos de planificación cooperativa de recursos energéticos. Universidad del Norte. 2008. ISBN: 978-958-8252-84-1
HERRERA, Germán. Análisis de Modelos de Planificación Colaborativa en la Cadena de Suministros: Una Revisión de la Literatura. Latin American and Caribbean Conference for Engineering and Technology. [En línea]. 2014. [Consultado en Febrero, 2017]. Disponible en: http://www.laccei.org/LACCEI2014-Guayaquil/RefereedPapers/RP022.pdf.
KUMAR, Kuldeep. Technologies for supporting supply chain management. Communications of the ACM. 2001. Vol. 44, No. 6. p. 58-61.
LARIO, Francisco., and PÉREZ, David. Gestión de Redes de Suministro (GRdS): sus Tipologías y Clasificaciones. Modelos de Referencia Conceptuales y Analíticos. IX Congreso de ingeniería de organización. Gijon. 2005. ISBN 84-96476-40-5. p. 163
MIN, Soonhong., ROATH, Anthony., DAUGHERTY, Patricia., GENCHEV, Stefan., CHEN, Haozhe., and ARNDT, Aaron. Supply chain collaboration: what’s happening?. International Journal of Logistics Management. 2005. Vol. 16. No. 2. p. 237–256.
SANA, Shib., HERRERA, Germán, and ACEVEDO, Jaime. Collaborative Model on the Agro-Industrial Supply Chain of Cocoa. Cybernetics and Systems an International Journal. 2017. Vol. 48. No. 4. p. 325 – 347.
STACKELBERG, Heinrich. The Theory of the market Economy. Springer-Verlag, Berlin, Oxford University Press. 2007.
STADTLER, Hartmut. Supply chain management and advanced planning –basics, overview and challenges. European Journal of Operational Research. 2005. Vol. 163. No. 3. p. 575-588.
1. PhD(c) Ingeniería Mención en Industrial. M.Sc. en Ingeniería con Énfasis en Industrial. Docente investigador de la Fundación Universitaria Tecnológico Comfenalco. Grupo de Investigación CIPTEC. Cartagena-Colombia. herreravg@tecnocomfenalco.edu.co
2. Magister en Gestión Logística. Escuela Naval de Cadetes Almirante Padilla. Cartagena–Colombia. heinermarrugocermeno@gmail.com
3. Desarrollado por ARKI Consulting and Development