

 Vol. 38 (Nº 50) Año 2017. Pág. 27
Vol. 38 (Nº 50) Año 2017. Pág. 27
Ernesto VARELA Arregocés 1; Emiro DE-LA-HOZ-FRANCO 2; Eduardo DE-LA-HOZ-CORREA 3; Carlos FAJARDO Toro 4
Recibido: 12/06/2017 • Aprobado: 22/07/2017
2. Fundamentals and related work
7. Recommendations and future works
ABSTRACT: The query algorithms in search engines use indexing, contextual analysis and ontologies, among other techniques, for text search. However, they do not use equations due to their writing complexity. NOMAT is a prototype of mathematical expression search engine that seeks information both in thesaurus and internet, using ontological tool for filtering and contextualizing information and LaTeX editor for the symbols in these expressions. This search engine was created to support mathematical research. Compared to other Internet search engines, NOMAT does not require prior knowledge of LaTeX, because has an editing tool which enables writing directly the symbols that make up the mathematical expression of interest. The results obtained were accurate and contextualized, compared to other commercial and no-commercial search engines. |
RESUMEN: Los algoritmos de consulta de los motores de búsqueda utilizan indexación, análisis contextual y ontologías, entre otras técnicas, para la búsqueda de texto. Sin embargo, no utilizan ecuaciones debido a su complejidad de escritura. Nomat es un prototipo de motor de búsqueda de expresión matemática que busca información tanto en tesauro como en Internet, utilizando la Herramienta ontológica para filtrar y contextualizar información y editor de látex para los símbolos de estas expresiones. Este buscador fue creado para apoyar la investigación matemática. En comparación con otros motores de búsqueda de Internet, Nomat no requiere conocimientos previos de látex, ya que cuenta con una herramienta de edición que permite escribir directamente los símbolos que componen la expresión matemática de interés. Los resultados obtenidos fueron precisos y contextualizados, en comparación con otros motores de búsqueda comerciales y no comerciales.
|
According to (Berners-Lee,Hendler & Lassila, 2001), when the World Wide Web was officially presented to the world in the early 90's, it was evident the absence of contexts in the searches, and although currently there are some progress in this regard, valuable time is still being lost in the process, since the web was based since its inception in processing documents that will be read by humans and not necessarily understood by computers.
The need to extract specific information from texts is a common action that is related to natural language processing, which involves the application of lexicography and computational semantics, text mining and implementation of machine learning techniques based on linguistic patterns, all in the context of the semantic web.
On the web there are investigations containing a varied repertoire of mathematical expressions; retrieving such information can become a really wasteful task, due to the limitations of existing browsers, which mostly only allow the search for textual information. However, there are some proposals such as: query language for the search Math formulas - MQL (Guo, Su, Li, An & Cui, 2013) and FDS maintenance algorithm of FDS based mathematical expressions index (Yang & Tian, 2014). In addition (Nghiem, Kristianto, Topic & Aizawa, 2014) make an interesting comparative analysis of categories such as (i) mathematical search that is presentation based and (ii) mathematical research that is content based by describing a number of mathematical expressions search tools for each category.
Some of these search tools use a repository of publications of mathematical formula (where the equations are encoded in MathML, OpenMath or LaTeX format), others perform the query supplying text strings (representing mathematical expressions) or images (containing equations) to a search engine on the web. Although these three alternatives mean a headway in processes of publication searches with mathematical expressions both in repositories (thesaurus) and the web, their query strategies are not efficient in terms of identification of the semantic context of the expressions; deficiency which was corroborated by searching for mathematical expressions of some complexity (with special symbols, for example: summations, derivatives and integrals).
The work described here in the first instance required an exploration of the conceptual foundations that supports this research and the projects pertaining to this proposal. This document also comprises a detailed description of the methodology used, the proposal at the heart of this research and its validation in various testing scenarios, in which the results obtained by NOMAT are compared to other search engines. The paper ends with conclusions and projection of future work.
This section describes the fundamentals of the proposed study (the Semantic Web, Ontologies and the defining context that determines the relevance of internet searches) reviewing research references, which have cemented the theoretical basis openly accepted by the scientific community, in relation to the contextual Internet search.
The semantic web according to (Berners-Lee et al 2001), is a data network that can be processed directly or indirectly by machines. (Sheth, 2013), defined as an online semantic knowledge management for product design based on product engineering ontologies, a theory of social agentivity and its integration into the descriptive Ontology for linguistics and cognitive engineering. World Wide Web Consortium defines the architecture of the semantic web, (see Figure 1) through a model of seven (7) levels (resources, documents auto syntactical description, resource description, vocabulary ontologies, logical rules, tests and confidence), which are described in (Berners-Lee et al 2001). Complementarily levels contain a number of basic elements that constitute the semantic web (XML, RDF, PICS, Ontologies and Agents), Table 1, also define by World Wide Web Consortium, describes each one of them. It is important to point out that this research focuses on the level of ontology vocabulary.
Ontology depict knowledge domains through these components: classes, instances, relations, functions, axioms, annotations, inheritances and derivations, according to (Guzmán Luna, López Bonilla & Torres, 2012) and (Contreras & Martínez, 2007). This is consistent with the indicated by (Neches et al 1991), (Gruber, 1992) and the World Wide Web Consortium W3C. Regarding the use of ontology for the representation of a domain, design decisions must be made concerning the clarity, consistency and extensibility. The most relevant ontology repositories according to (Chen et al, 2005) are: SOUPA (Standard Ontology for Ubiquitous and Pervasive Applications), whose aim is to guide developers, who do not have experience in knowledge representation, to quickly build applications based on ontologies. Another repository models are CONON (Ontology based context modelling and reasoning using OWL), which provides an ontology-oriented context-sensitive applications (Wang, Gu, Zhang y Pung, 2004); FIPA (Foundation for Intelligent Physical Agents) is used for expressing the capabilities of different devices in ubiquitous computing systems (IEEE Computer Society – FIPA, 2015); GUMO (The General User Model Ontology) ontology for the modelling of general concepts (Heckmann, Schwartz, Brandherm & Kröner, 2005).
Figure No 1, Architecture of the Semantic Web,
according to World Wide Web Consortium
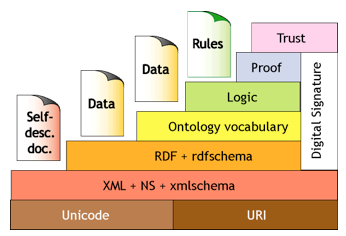
Source: http://www.w3.org/2001/09/21-orf/hagino-sw/swlevels.gif
-----
Table No 1. Elements of the Semantic Web
XML |
Extensible Markup Language is a coding language that facilitates the distribution of complex documents by Internet, generating a more semantic structure on the Web. It allows web designers to use their own markup- tags. XML is a subset of SGML (Standard Generalized Markup Language) that defines a text format designed for the transmission of structured data. As a subset of SGML, it retains the validation characteristics, structure and extensibility, because it is a meta-markup language that describes both the definition of labels as well as the structural relationship between them. |
RDF |
Resource Description Framework, describes the network resources (pages, people, devices, objects, images, et al), by adjusting the necessary conditions for the consultation to become part of the characteristics defined in the system, so that does not generate ambiguities, by the use of URI, which allows encoding, exchange and processing of metadata that have been standardized. This model transforms statements of resources in terms of the form subject-predicate-object (or triplets), according to (W3C, 2015). The most popular implementation of RDF are the pages RSS (Really Simply Syndication) that are grounded in XML format for sharing content on the Web. |
PICS |
The Platform for the Internet Content Selection, allow view specific characteristics of files, depending of the community user is located. These are infrastructures that associate labels with Internet content, in terms of privacy, license, restricted access and others. This mechanism according to (Universidad Politécnica de Valencia, 2015), consists of: (1) tags (metadata that indicates the value of a document), (2) valuation services (organizations, groups or persons performing an assessment), and (3) profiles (rules that are established by the user to define the filter and avoid receiving unwanted documents). |
Ontologies |
Ontologies are collections of statements written in a language such as RDF, which defines the relationships between concepts and specify logical rules for reasoning with them. Computers interpret the meaning of semantic data from a web site by following links with specified ontologies. (Fenoll & Luque, 2006). |
Agents |
They are considered tools of increasing use, due to the evolution of Telematics (Uribe Tirado, 2015). In the semantic web agents fulfil the function of searching for services, communicating each other the exact function they perform, and what data they need to receive. |
There are multiple applications of ontologies, for example: (Rovetto & Mizoguchi, 2015) developed a medical Ontology RFM and its interaction with two other ontologies of the same type, and it includes causality as additional element to ontology giving strength to the consultation and classification of diseases and biological processes in natural language. (Cristani & Ferrario, 2014a) shown the use of Ontology in the field of Artificial Vision and progress in this respect. It is mentioned the development of a methodology for object recognition, from its characteristics and how they are feeding the used ontology. On the other hand, (Cristani & Ferrario, 2014b), creates an ontology that would handle the information obtained from devices with artificial vision and intelligent agents. This ontology helps to the creation of a complex socio-technical system, used as support for decision-making is outlined. (Setti, Porello, Ferrario, Abduljalil & Cristani, 2015) use tools of lexicography and computational semantics as remarkable fact, as well as a qualifying ontology of images from the Internet image repository. However, as most of the images are uploaded for different purposes, indexing becomes a complex procedure, with which nevertheless, important improvements were obtained compared to other standard methods of information search. Another ontology application has been developed by (Park & Musen, 1998), where in their work it is outlined the reuse of an ontology designed in Protegé to revive the knowledge base of a virtual machine.
One way to highlight the richness of relationships that can maintain a definition regarding a term, is to consider that both are configured in a structure called the Defining Context (DC), understood as a textual fragment where a term and its definition is introduced (Alarcón & Sierra, 2003). The automatic extraction of textual terms has been extensively investigated (Cabré, Estopá & Vivaldi, 2001) and currently poses no problem, however the concept extraction involves a fairly complex activity because they handle different approaches according to the limits and characteristics of their feasible definitions.
A Defining Context (DC) presents various structures, but essentially it has elements such as: term, definition, defining verbal predicate, defining reformulation markers, defining typographical markers, pragmatic patterns, co-reference and anaphora relationships that are established between the defined term and these listed units. The identification of these components allows the distinction of syntactic and semantic patterns of behavior that facilitate obtaining data for search and classification of definitions. Figure 2, taken from (Alarcón & Sierra, 2003), identifies the components of a DC.
Figure No 2. Example of a Defining Context (DC)
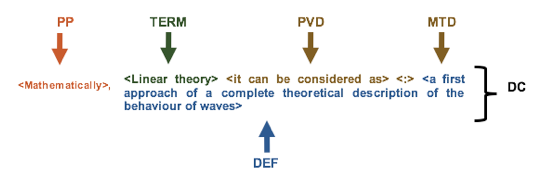
The most common problems presented by web queries, according to (Baeza-Yates & J. Pino, 2006) are: the volume of information, spam in content and links, languages in which pages were designed, retrieval of multimedia information, the poor quality of the user interface and the poverty in displaying query results. As for the context in search engines, according to (Melucci, 2005) this is not caught in indexing time, and not used in recovery time; this makes the result of the query inaccurate and as a result of this, the user ends up getting mixed information provoking that spends more time doing the reading the retrieved pages, leading to abandonment of the search without obtaining the desired result.
In (Valencia, 2007), some related approaches have been raised: the calculation of the relevance of users, analysis of documents viewed or edited by the user, improvements in technology used in the search, implicit and explicit feedback user’s categorization and consultations, among others.
The contextual analysis of an equation or a mathematical expression is a rather complex issue to address because it alone does not make any sense, if it is not accompanied by an explanation that contextualizes those symbols (Garcés & Cobos, 2011). The same happens in a web query, when writing an equation in a browser it indicates the result of a list of addresses that do not guide much to the consultation process. In (Yokoi & Aizawa, 2009) it is pointed out that when consulting the mathematical expression on the web, it is obviated, and it is sought using the accompanying text, the name of the author(s) or otherwise, is treated as an image, using techniques such as machine-learning and pattern recognition.
If a browser addresses the interpretation of an equation without aspects to guide the search context, not only would it be facing a Touring-machine in its purest state, but the results would be extremely ambiguous, mixed and meaningless. In fact, usually an equation cannot be written in the space of consultation of the usual search engines, because the keyboard of the computer equipment, fixed or mobile does not have all the symbolism for it.
In this line of work there are search tools and more oriented towards the field of mathematics and physics, including "MathSciNet" of the American Mathematical Society which seeks scientific material with enough precision; this tool has components that help making the request specifically, but it does not do a search from equations and clear text.
Although the search for answers "Wolfram Alpha" (Wolfram Research Inc, 2015), seems to provide solutions to problems, what it really makes is a query in its own repository of information, fed by a large team of mathematicians that solve a big number of exercises; and although in this case, the equations are allowed to be written (not precisely but with their own commands), this tool does not query the web directly.
The search strategies of mathematical expressions defined by (Nghiem et al, 2014) are focused on content and presentation based on mathematical search. The first strategy uses a system of mathematical search based on documentation contained in the state of the art in the field of mathematics, while the second one uses the semantic enrichment of mathematical expressions to convert those expressions in their content forms and thus perform the search using them.
As regards presentation-based search systems in Springer LaTeXSearch (Springer, 2015), it provides a free service to search LaTeX code within the scientific literature of a repository, allowing users to locate and visualize scientific articles that contain equations in specific LaTeX code or equations that contain LaTeX code similar to Latex chain originally introduced. On this category it is also included the search engine of mathematical expressions MathDeX or MathFind (Munavalli & Miner, 2006), developed by Design Science. It breaks the mathematical expression to be searched in a sequence of mathematical fragments in text encoded in MathML, and then it performs the consultation with the text strings as a normal text search.
The National Institute of Standards and Technology - NIST developed the Digital Library of Mathematical Functions - DLMF (NIST, 2015) and (Miller & Yousse, 2005), which is a mathematical data base available on the Web, and uses two approaches to finding mathematical formulae in DLMF. For the first approach, it is used a serialization and standardization textual language called TexSN (Youssef, 2005), whereby the consultations are modified before processing, then the search is performed to find the mathematical expressions that match the query exactly, and finally mathematical formulas similar to those initially raised are recovered.
The second is a search system that treats each mathematical expression as a document that contains a set of mathematical terms (Youssef, 2007). The document uses new classification metrics for relevance and generation techniques of description far superior to conventional metrics. Other search systems representative of mathematical expressions that fit this category are Math Indexer and Searcher (Sojka & Liska, 2011), EgoMath (Misutka & Galambos, 2011), and ActiveMath (Siekmann, 2015).
Moreover, regarding the search content-based, the Wolfram Functions site (Wolfram Research Inc, 2015) is highlighted. This site is a collection of accessible mathematical formulae on the Web, enabling the search for mathematical expressions in a data repository, where similarity search methods based on MathML are used; however, the content-based search is only available for a number of predefined constants, operations and function names.
The MathWebSearch system from (Kohlhase & Sucan, 2006) and (Kohlhase & Prodescu, 2011) is a content-based mathematical formula search engine that first converts all formula to content tags encoded in MathML and then uses substitution trees to build the search index. The authors claim that the search times are fast and do not vary significantly despite the increased size of the index.
On the other hand, MathGO! Search (Adeel, Cheung & Khival, 2008) is a system that uses regular expressions to generate indexing of keywords, improving data recovery through the clustering of the contents of mathematics formulas using K-SOM, K-means and AHC. Experiments realized with a collection of 500 mathematical documents were made, reaching 70 percent accuracy. (Yokoi & Aizawa, 2009), use a mathematical expressions similarity search method that is specifically adapted to the tree structures used in MathML; the experimental results showed that the proposed scheme provides a flexible system for the search of mathematical expressions on the Web, however, the calculation of similarity is the bottleneck of the search when the size of the database increases, plus the system only recognizes symbols and does not see the actual values or strings assigned to it.
The search engine of mathematical expressions called SYSTEM (Nguyen, Chang & Hui, 2012) can handle both text typed by keyboard as well as mathematical expressions. That is possible using a machine model of finite states for feature extraction, and a framework of representation which captures the semantics of mathematical expressions. For classification, the developers used a passive-aggressive on line learning binary classifier. The experimental results were obtained using the dataset (MathOverflow, 2015).
Regarding the references related to the research approach proposed here, some allow writing simple mathematical expressions for their subsequent search, but none of them allowed writing complex mathematical expressions. Additionally, the results obtained by the searches, in the vast majority of consulted tools are not contextualized, reflecting that information in some cases is not consistent with the objective of the searches of interest.
Based on the above, concluded that the problem of contextual interpretation of mathematical equations in a browser lies in the following aspects: i) Reading of the equation: browsers have not been developed to work with the grammar of the equations. ii) The interpretation of context: equations are meaningless by themselves, they need a complementary text that provides sense and usually browsers are not designed for it. iii) Make the web query: the results of Web queries are not the best, due to the high volume of information on the Internet; if the query is not contextualized, the results are deficient.
The proposed study is documentary, experimental and applied. This is because the research is based on a review of various documentary sources about the framework on which this work is based. On the other hand, given the characteristics of the object of study, it can be considered controlled experimental-inductive - because it uses a dynamic analysis in where the behavior of the software prototype is observed. This prototype allows the design of queries using mathematical expressions from differential and integral calculus as well as differential equations, with contextual elements, measuring the effectiveness of consultations made on the Internet and contrasting these results with searches made in nine (9) of the most popular Internet search engines.
Mathematical Ontological Browser – NOMAT, for its acronym in Spanish “Navegador Ontológico Matemático”, is presented for problems of searching mathematical expressions, both in equations inside a specific data repository and internet repositories. In this document, an architecture is presented. The visual design of the prototype and your implementation, is shown in section 5. Additionally, the validation of its functional effectiveness is presented, through different simulated scenarios.
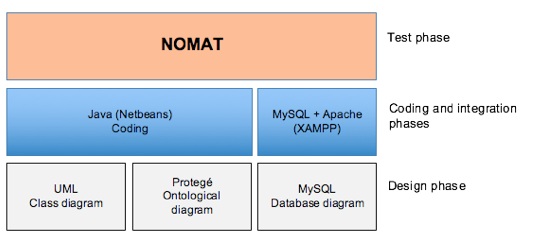
The tool proposed has been developed in 4 phases, following an iterative model. The phases were shown in Figure 3, are: i) analysis and design, ii) Implementation, iii) integration and vi) testing. The design was made in Unified Model Language - UML (see Figure 4).
Initially the class diagram of the Ontology and the database are made with UML. The Ontology was designed using the framework of the tool Protegé (Stanford University, 2015) and the database was designed to store the information managed in the repository (thesaurus). Subsequently, the implementation of the methods of each class was made, doing an integration between the ontological model designed in Protegé and the databases implemented in MySQL.
For this integration was necessary the installation MySQL and APACHE server using XAMPP tool. The coding was made in Java using Netbeans as development environment. Finally, different white and black box tests to validate has been realized, to test internal and external functional requirements of the application developed.
Figure No 3. Phases and tools used in the development of the proposal NOMAT
------
Figure No 4. UML class diagram of the proposal NOMAT
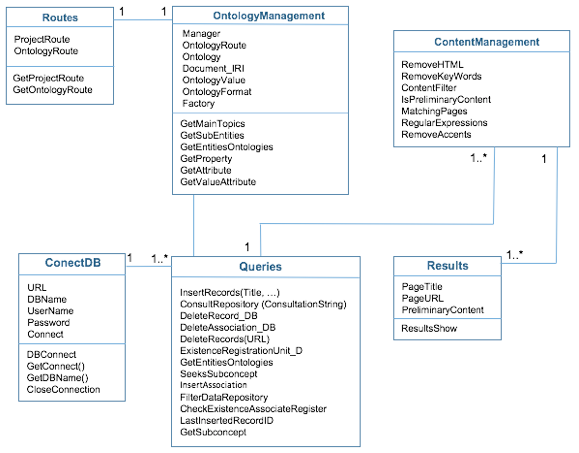
Tables 2, 3 and 4, show details of UML diagram NOMAT, describing each of the attributes and methods that conform the classes.
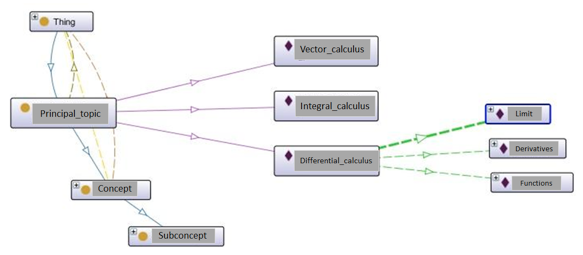
The ontology was constructed in a hierarchy of three levels (see Figure 5). The first level is the main class, called main_topic, which consists of three mathematical topics referred: diferential_calculus, integral_calculus and vectorial_calculus. The second level is a subclass called concept, which represents diferential_calculus topic (precedes it in the hierarchy), consists of three topics (1) Limit, (2) Derivative and (3) Functions. The third level of the hierarchy is a class derived from the concept class, called subconcept, so that the functions topic (precedes it in the hierarchy), consists of the topics (1) graphic_function, (2) exponential_function, (3) logarithmic_function, (4) linear_function, (5) inverse_function and (6) quadratic_function.
Table No 2. Attributes and methods OntologyManagement class
OntologyManagement Class |
|||
Attributes |
Type |
||
Manager: |
OWLOntologyManager |
||
OntologyRoute: |
Routes |
||
Ontology: |
OWLOntology |
||
DocumentIRI: |
IRI |
||
OntologyValue: |
IRI |
||
OntologyFormat: |
PrefixOWLOntologyFormat |
||
Factory: |
OWLDataFactory |
||
This class runs through the Ontology NOMAT in order to extract topics and subtopics of the mathematics area that the software will consider to search, find and store web content related to these concepts. |
|||
GetMainTopics method |
GetSubEntities method |
||
Input parameters: |
None (String) |
Input parameters: |
Individual_Name (String) Relation (String) Attribute (String) |
Type Method: |
Function |
Type Method: |
Function |
Return Value: |
Hashmap |
Return Value: |
Hashmap |
Returns all topics contained in the ontology NOMAT. |
Return all subtopics of each topic included in NOMAT Ontology. |
||
-----
Table No 3. Attributes and methods of ContentManagement class
ContentManagement Class |
|||
Attributes |
None |
||
This class filters the contents of the pages found by NOMAT; in this class comparisons and filtering the contents of each page found with the search string provided in LATEX by the user in the search menu are made. |
|||
RemoveHTML method |
RemoveKewWords method |
||
Input parameters: |
String (String) |
Input parameters: |
String (String) |
Type Method: |
Function |
Type Method: |
Function |
Return Value: |
Hashmap |
Return Value: |
Hashmap |
This method removes HTML text words within the captured information that are irrelevant to the content comparison. Here the HTML tags that each website page has (in the contents previously found) are filtered. |
This method removes the text strings within the captured information that are irrelevant to the content comparison. Here are filtered commands color font styles and visual appearance of the contents found before looking for similarities to our text string in LATEX provided. |
||
ContentFilter method |
IsPreliminaryContent method |
||
Input parameters: |
PreliminaryResults (Hashmap) Entered string (String) |
Input parameters: |
PreliminaryResults (String) Contents (Arraylist <String>) |
Type: |
Procedure |
Type: |
Function |
Return Value: |
Hashmap |
Return Value: |
Boolean |
This method performs the logical comparison to determine string matches with a high degree of similarity to obtain the Web page where the content search is performed. This feature relies on others to do content filtering. |
This method iterates through the contents found on a given page in order to find the string in LATEX supplied by the user and to determine if the page containing that string allows the capture of that result. |
||
-----
Table 4. Attributes and methods of the Consultations class
| Consultation Class | |||
Attributes |
None |
||
This class provides access to topics and subtopics in the repository of information, performs queries to the database in order to check contents and page views, also performs insertions and associations in the database NOMAT. |
|||
InsertRecords method |
ConsultRepository method |
||
Input parameters: |
Title (String) PreliminaryContent (String) BasicURL (String) ComposedURL (String) |
Input parameters: |
ConsultationString |
Type: |
Function |
Type: |
Function |
Return Value: |
None |
Return Value: |
LinkedHashMap <Integer, String> |
This function allows to store an obtained result of a query, performed by the string in LATEX supplied by the user. |
This function allows to consult directly the database that contains web pages related to a previous query without the need to consult on the web new pages with the captured.information. |
||
-----
Figure No 5. Ontological diagram of NOMAT
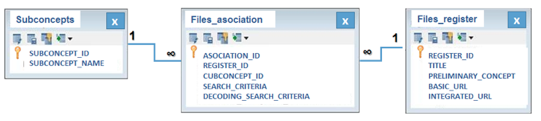
The NOMAT database can store successful search results. This database will later allow the retrieval of previously stored queries. Its structure is constituted by three tables: (1) Subconcepts, (2) Association_Records and (3) Records (see Figure 6). The Subconcepts table stores the name and code of each one of the topics previously indicated in the ontology, in this case are: (1) Graphic_Function, (2) Exponential_Function, (3) Logarithmic_Function, (4) Linear_Function, (5) Inverse_Function and (6) Quadratic_Function.
The Records table stores information of pages returned by the query; the data stored for each found page are: (1) the registration code, (2) page title, (3) preliminary content, (4) root URL of page and (5) composed URL of page.
The Association_Records table stores the relationship between the subconcept looking for records and pages retrieved by the search, their fields are: (1) code of association, (2) registration code, to connect it with the Records table, (3) code of subconcept, to connect it with the Subconcepts table (4) search criteria or sought equation and (5) the search criterion decoded or the interpretation that the search in LATEX format makes.
Figure No 6. Diagram of the NOMAT database
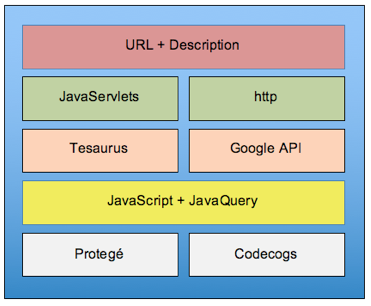
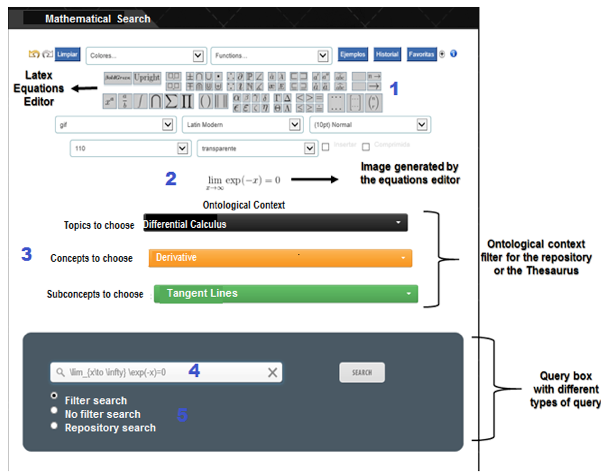
It has five layers (see Figure 7), on layer 1 the application receives the query issued by the user using the interface NOMAT, from which sought equations are captured as input parameters, it’s possible indicate the categorical context of the mathematical expression. This is introduced by an equation editor LATEX integrated to NOMAT called Codecogs (Codecogs, 2015). Indicating the ontological filter, it's possible to select if the search will be made (1) with or (2) without filter, or (3) in the repository.
When the search is done in the repository, the Protegé tool is used to access the predesigned ontology and thus perform the indicated filtering in the categorical context of the search. In both cases (web or repository) integration between JavaQuery and JavaScript (layer 2) allows send the search to the Google kernel by an API or Thesaurus (layer 3). Then consultation response is sent, displaying information through JavaServlets (if it was from the Thesaurus) or http (if it was from the Web), which corresponds to layer 4. NOMAT displays the pages found, showing their URLs and a brief description of each (layer 5), for the user to consult them according to their interests.
Figure No 7. NOMAT Architecture
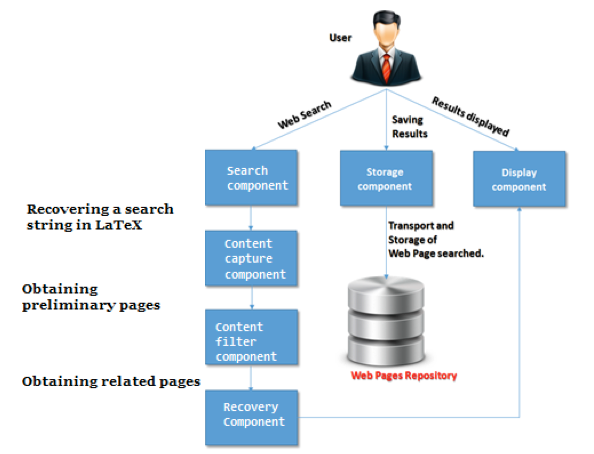
The Ontological Mathematical Browser, has three basic features: (1) query in repository and web, (2) storing the results of searches in own repository (thesaurus) for future references and (3) results display (see Figure 8).
Figure No 8. NOMAT functional model
The NOMAT graphical interface (see Figure 9) consists of: (1) integrated mathematical editor Codecogs, that allows write the construction of mathematical expressions (converting text to Latex Format), (2) categorical context of equation, which is captured from a series of dropdown lists that are part of interface, where is selected topic, concept and subconcepts that define the ontological filtering and (3) a menu of search options for selecting the type of search to do (with filter, without filter or in a repository). Once the search parameters are indicated a submit button named “search” is used.
Figure No 9. Graphical user interface of NOMAT browser.
Component search in the repository or in the internet
Once search results have returned, relevant pages can be stored in a thesaurus repository, by clicking the button that looks like a floppy disk (see Figure 10).
Figure No 10. NOMAT output visualization component

The search criteria are stored in the association records table and the URLs of pages obtained after the search are stored in the records table. The pages stored in thesaurus can be retrieved accessing from NOMAT main interface, selecting option to repository search in the search options menu (see Figure 9).
The display result component takes the array of the results and runs in each of their positions in order to obtain the values and enter them in a results pager (see Figure 11). Pager shows the different pages related to the search one on one, in an organized sequence with the concerning information of the source where it was found the original web page, the title of the web page and preliminary content.
Figure No 11. Interface where the results of the searches performed are displayed
The functionality of NOMAT was validated, applying an experimental scenario in which the expression 2x + 3y = 1 is sought on Google®, as a result 5.47 million URLs in 0.29 seconds were showed. Although the results were essentially mathematical type, the verified pages showed the expression with a negative sign. The same search was made in Yahoo! ®, showing slightly more accurate results, as to the form of the expression consulted. In search engines AOL ®, Excite ® and Bing ® the results were very similar to Google.
In a second stage of experimentation, attempts were made to search for expressions involving symbols of integrals and differential equations, see 1 and 2.
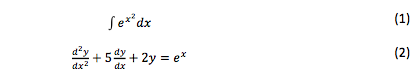
Nevertheless interfaces used in search engines do not allow writing of such expressions unless the user writes directly in LATEX. Thus the search was not possible. Evidently, the vast majority of search engine users do not have the technical knowledge to express an equation directly in LATEX format. In the NOMAT proposal it’s not necessary to write the expression in LATEX, since it has been integrated to the interface, a component that allows to construct in an intuitive way and in a graphical environment, the equations to look for, see figure 9.
The review of the state of the art showed that there are web browsers for the search of mathematical expressions, some allow for consultation on specific repositories but not on the web. Additionally, the writing query is performed in a mathematical expressions code language as LaTeX, MathML, TexSN, typed by keyboard or by attaching a document with the expressions, but it was not found evidence of intuitive friendly-user graphical interface in web browsers, that help to write expressions, for users can search without knowledge of a mathematical text editor (see Table 5).
Table No 5. Contrasting functionality of web browsers of mathematical expressions
Web Browser |
Repository |
Web |
Input Method |
Observations |
LaTeXSearch (Springer, 2015) |
Yes (Springer) |
No |
LaTeX Código |
Just search scientific articles |
MathDex or MathFind (Munavalli & Miner, 2006) |
Not provided |
Not provided |
MathML Código |
|
DLMF-NIST (NIST, 2015) & (Miller & Youssef, 2003) |
Yes (DLMF) |
No |
(1) TexSN Code (2) Document Attached |
|
Wolfram Web site Functions (Wolfram Research Inc, 2015) |
Yes (Own Wolfram Functions) |
No |
MathML Code |
|
MathWebSearch (Kohlhase & Sucan, A search engine for mathematical formulae, 2006) & (Kohlhase & Prodescu, Mathwebsearch at NTCIR-10, 2013) |
Not provided |
Yes |
MathML Code |
|
MathGO! Search (Adeel, Cheung, & Khival, 2008) |
yes |
No |
Not provided |
|
MathDA (Yokoi & Aizawa, 2009) |
yes |
Yes |
MathML Code |
Problems when it increases the size of the dataset |
System Nguyen (Nguyen, Chang, & Hui, 2012) |
Yes (MathOverFlow) |
Not provided |
(1) input for Keyboard (2) mathematical expressions in finite state machines |
|
NOMAT |
Yes (Own Thesaurus) |
Yes |
(1) Graphical Interface (2) LaTeX Code |
|
After a theoretical review of issues related to Semantic Web and the Defining Context, including the mathematical context regarding the search for mathematical expressions, it can be asserted that a single expression is meaningless if there is not clear text to contextualize. In addition, the mathematical context is a broad topic which implies certain difficulties to be implemented in conventional computer systems.
In the other hand, for the correct functioning of NOMAT, it’s necessary to use other applications granting it a hybrid character and add several features that in future versions will allow the integration of additional utilities, such as the use of intelligent agents to refine query techniques. The inclusion of other web search strategies through diverse language codes for editing mathematical texts and the implementation of new ontologies to strengthen the Defining Context and a more user-friendly interface.
Finally, regarding experimentation, the results were summarized in the Table 5. the results obtained are similar, to the extent that the expressions simple can be typed with keyword. However, when trying to search differential equations or expressions with integral or other symbols, none of the commercial web browsers allowed the transcription of the mathematical symbols, aspect that was accomplished by NOMAT using an interface (API Codecogs) as a LaTeX code transcriber and producing as a result web pages edited with this tool. This fact demonstrates that LaTeX can be used as a scientific text editor and as a language editor for browsing. Hence the NOMAT Browser proposal is presented as a functional tool (For using Google API and LATEX Codecogs) with improvements in the effectivity of Web search regarding conventional Web Browsers.
In the majority of mathematical expressions web search solutions that exist, the query is focused on an exact match or in the use of metadata to extract the semantical context that gives contextual meaning to the mathematical expression of interest, classifying the information found through basic statistical methods, such as counting matches between raised mathematical expressions and the occurrences of mathematical expressions substructures not paying enough attention to the coincidence of the notation, that is, the structural similarity and mathematical semantics, between the expression to be searched and the expression found. To solve this situation, (Zhang & Youssef, 2014) developed an approach that aims at evaluating the similarity in the mathematical expressions searches should be used. This is an interesting research tendency that will improve the web search of mathematical expressions.
After designing the prototype, checking different web search scenarios and as a result of experimentation and contrasting the obtained results, the following recommendations emerged and need to be considered:
Develop a solution that does not require Google API, allowing more control in defining the filtering context for this search and a web browser that implements search algorithms specially designed for working with LaTeX, analysing its effectiveness in the web and information repositories (thesaurus).
Implement search algorithms using intelligent agent technology to analyse network behavior. These algorithms could use hierarchical self-organizing maps and multiobjective optimization techniques, such as those proposed in (De-La-Hoz-Franco, De-La-Hoz-Correa, Ortiz, Ortega, & Martinez, 2014).
Promote to the W3C the standardization of mathematical documents on the web through the implementation of LaTeX, which would contribute to the design of much more complex web searches.
Design specialized tools to perform the web search of expressions in the field of chemistry and physics.
Improve the accuracy of the results obtained by implementing similarity criteria between the searched mathematical expressions and the information found.
Adeel, M., Cheung, H., & Khival, S. (2008). Math go! prototype of a content based mathematical formula search engine. Journal of Theorical and Applied Information Technology , 1002-1012.
Alarcón, R., & Sierra, G. (2003). El rol de las predicaciones verbales en la extracción automática de conceptos. Estudios de lingüistica aplicada, 129-144.
Baeza-Yates, R., & Pino, J. (2006). Towards formal evaluation of collaborative work. Information Research.
Berners-Lee, T., Hendler, J., & Lassila, O. (2001). The Semantic Web: A new form of Web content that is meaningful to computers will unleash a revolution of new possibilities. Scientific American, 1-4.
Cabré, T., Estopá, R., & Vivaldi, J. (2001). Automatic term detection. A review of current systems. . Recent Advances in Computational Terminology, 53-87.
Chen, H., Finin, T., & Joshi, A. (2005). SOUPA: Standard Ontology for Ubiquitous and Pervasive Applications. Ontologies for agents: Theory and experiences, 233-258.
Codecogs. (7 de December de 2015). Codecogs LaTeX. Obtenido de https://www.codecogs.com/latex/eqneditor.php
Contreras, J., & Martínez, J. (2007). Tutorial de ontologías. SEDIC - Asociación Española de Documentación e Información.
Cristani, M., & Ferrario, R. (2014). Multiagent socio-technical systems. An Ontological approach. En T. Balke, F. Dignum, M. Van Riemsdijk, & A. Chopra, Coordination, Organizations, Institutions, and Norms in Agent Systems IX (págs. 42-62). Switzerland: Lecture Notes in Computer Science - Springer International Publishing.
De-La-Hoz-Franco, E., De-La-Hoz-Correa, E., Ortiz, A., Ortega, J., & Martinez, A. (2014). Feature selection by multi-objective optimisation: Application to network anomaly detection by hierarchical self-organising maps. KBS - Knowledge-Based Systems. Knowledge-Based Systems, 71, 322-338.
Garcés, S., & Cobos, C. (2011). Metabuscador web basado en la información del contexto y el filtrado colaborativo. Revista UIS Ingenierías.
Guo, W., Su, W., Li, L., An, N., & Cui, L. (2013). MQL: A mathematical formula query language for mathematical search. 2013 IEEE 16th Internacional Conference on Computacional Science and Engineering (págs. 245-250). IEEE Computer Society.
Gruber, T. (1992). Toward Principles for the Design of Ontologies used for Knowledge Sharing. International Journal of Human and Computer Studies, 907-928.
Guzmán Luna, J., López Bonilla, M., & Torres, I. (2012). Methodologies and methods for building ontologies. Scientia et Technica, 133-140.
Heckmann, D., Schwartz, T., Brandherm, B., & Kröner, A. (2005). GUMO the General User Model Ontology. Lecture Notes in Computer Science - Springer , 428-432.
IEEE Computer Society - FIPA. (3 de December de 2015). http://www.fipa.org/. Obtenido de The Foundation for Intelligent Physical Agents.
Kohlhase, M., & Sucan, I. (2006). A search engine for mathematical formulae. En J. Calmet, T. Ida, & D. Wang, AISC 2006 - LNCS (LNAI) (págs. 241-253). Springer Heidelberg.
Kohlhase, M., & Prodescu, C. (2013). Mathwebsearch at NTCIR-10. National Institute of Informatics Testbeds and Community for Information access Research 10 (NTCIR-10), 675-679.
MathOverflow. (7 de December de 2015). MathOverflow. Obtenido de http://mathoverflow.net/
Melucci, M. (2005). Context modeling and discovery using vector space bases. Proceedings of the AAAI Spring Symposium on Quantum Interaccion, 808-815.
Miller, B., & Youssef, A. (2003). Technical aspects of the digital library of mathematical functions. Annals of Mathematics and Artificial Intelligence, 121-136.
Misutka, J., & Galambos, L. (2011). System description: EgoMath2 as a tool for mathematical searching on wikipedia.org. En J. Davenport, W. Farmer, J. Urban, & F. Rabe, MKM/Calculemus - LNCS (págs. 307-309). Springer - Heidelberg.
Munavalli, R., & Miner, R. (2006). Mathfind: a math-aware search engine. Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (pág. 735). ACM.
Neches, R., Fikes, R., Finin, T., Gruber, T., Patil, R., Senator, T., & Swartout, W. (1991). Enabling Technology for Knowledge Sharing. AI Magazine, 36-56.
Nghiem, M.-Q., Kristianto, G., Topic, G., & Aizawa, A. (2014). Which one is better: Presentation-based or content-based math search? En S. Watt, J. Davenport, A. Sexton, P. Sojka, & J. Urban, Intelligent Computer Mathematics (págs. 200-212). Coimbra - Portugal: Springer Link.
Nguyen, T., Chang, K., & Hui, S. (2012). Amath-aware search engine formath question answering system. Proceedings of the 21st ACM International Conference on Information and Knowledge Management (CIKM 2012), 724-733.
NIST. (7 de December de 2015). National Institute of Standards and Technology: Digital library of mathematical functions. Obtenido de http://dlmf.nist.gov
Park, J., & Musen, M. (1998). Virtual Machine in Protégé: A Study of Software Reuse . Studies in Health Tecnology and Informatics, 644-648.
Rovetto, R., & Mizoguchi, R. (2015). Causality and the Ontology desease. Applied Ontology, 81-86.
Setti, F., Porello, D., Ferrario, R., Abduljalil, S., & Cristani, M. (2 de December de 2015). "Tell me more": how semantic technologies can help refining internet image search. Obtenido de Laboratory for Applied Ontology: http://www.loa.istc.cnr.it/sites/default/files/vigta13_ontoclass.pdf
Sheth, A. (2013). Semantic web: Ontology and knowledge base enabled tools, services and applications. IGI Global.
Siekmann, J. (7 de December de 2015). Activemath. Obtenido de http://www.activemath.org/eu/
Sojka, P., & Liska, M. (2011). The Art of Mathematics Retrieval. Proceedings of the ACM Conference on Document Engineering (págs. 57-60). Mountain View - CA: Association of Computing Machinery.
Springer. (1 de December de 2015). Springer LaTeX. Obtenido de http://www.latexsearch.com/
Stanford University. (s.f.). Protégé. Recuperado el 7 de December de 2015, de http://protege.stanford.edu/
Universidad Politécnica de Valencia. (3 de December de 2015). Web Semántica: Agentes Inteligentes. Obtenido de http://personales.upv.es/ccarrasc/doc/2003-2004/websemag/agentes.htm
Uribe Tirado, A. (3 de December de 2015). Acceso, conocimiento y uso de las herramientas especializadas de internet entre la comunidad académica, científica, profesional y cultural de la Universidad de Antioquía. Obtenido de e-LiS repository: http://eprints.rclis.org/6206/1/presentacion.pdf
Valencia, M. (2007). Categorización de consultas enviadas a un motor de búsqueda web. Tesis Doctoral. Valencia, España: Universidad Politécnica de Madrid.
Wang, X., Gu, T., Zhang, D., & Pung, H. (2004). Ontology based context modeling and reasoning using OWL. Second IEEE workshop on context modeling and reasoning, 18-22.
Wolfram Research Inc. (7 de December de 2015). Wolfram Alpha. Obtenido de http://functions.wolfram.com/
W3C. (3 de December de 2015). World Wide Web Consortium. Obtenido de www.w3c.es/Divulgacion/GuiasBreves/HojasEstilo
Yang, S.-Q., & Tian, X.-D. (2014). A maintenance algorithm of FDS based mathematical expression index. Proceedings of the 2014 International Conference on Machine Learning and Cybernetics (págs. 888-892). Lanzhou - China: IEEEXplore.
Yokoi, K., & Aizawa, A. (2009). An approach to similarity search for mathematical expressions using MathML. Czech Digital Mathematics Library, 27-35.
Youssef, A. (2005). Information search and retrieval of mathematical contents: Issues and methods. The ISCA 14th International Conference on Intelligent and Adaptative Sustems and Software Engineering, 100-105.
Youssef, A. (2007). Methods of relevance ranking and hit-content generation in math search. En M. Kauers, M. Kerber, R. Miner, & W. Windsteiger, MKM/Calculemus (págs. 393-406). Springer - Heidelberg.
Zhang, Q., & Youssef, A. (2014). An Approach to Math-Similarity Search. CICM 2014 - LNAI 8543 - Springer International Publishing Switzerland, 404-418.
1. MSc degree in Systems Engineering and Computer Science (2015) at Universidad Simon Bolivar (Barranquilla, Colombia), and the Specialist degree in Teaching and Research with emphasis on Mathematics in 2011 at Universidad Sergio Arboleda (Bogota, Colombia). Currently he is a full time professor at Universidad del Atlántico (Barranquilla, Colombia). His research interests are in the field of ontologies, search engines for mathematical expressions and the semantic web.
2. PhD degree in Technology of the Information and Communication (2016) and MSc degree in Systems Engineering and Networks in 2011 all from Granada University (Spain). Currently he is a full time professor and member of Software Engineering and Networks research group at Universidad de la Costa - CUC (Barranquilla, Colombia). His research interests are in the field of data mining and multiobjective optimization techniques. email: emiro.delahoz.franco@gmail.com
3. PhD degree in Technology of the Information and Communication (2016) and MSc degree in Systems Engineering and Networks in 2011 all from Granada University (Spain). Currently he is a full time professor and member of Software Engineering and Networks research group at Universidad de la Costa - CUC (Barranquilla, Colombia). His research interests are in the field of data mining and anomaly-based Intrusion Detection Systems using Machine Learning techniques.
4. PhD degree from the University of Vigo, Spain. He worked as an associate and full time professor at the Icesi University in Cali, Colombia from 1994 to 2001, and as an associate professor at the Computer Science Department of the University of Vigo from 2001 to 2010. He collaborates as researcher with the SING group (Computer Systems of New Generation) belonging to the University of Vigo and the IREHISA group belonging to the Universidad del Valle in Colombia. He serves currently as a full time professor at the School of Business Administration - EAN (Bogota, Colombia).