

 Vol. 38 (Nº 50) Año 2017. Pág. 13
Vol. 38 (Nº 50) Año 2017. Pág. 13
Sergey Viktorovich SHCHERBATYKH 1; Anna Yuryevna ROGACHEVA 2
Recibido: 04/07/2017 • Aprobado: 25/07/2017
ABSTRACT: The relevance of this study is due to the problem of continuing education in mathematics lessons, need to develop new methods of teaching within one of the lines of the school course of mathematics - a stochastic one, whose potential is able to exert a significant influence on the formation of the student's personality. Purpose of the study is to prove the necessity of realization of continuous stochastic education in school. Research methods: pedagogical experiment (forming and control stages), a method of statistical processing of quantitative results of the study. As a result of the study, the problems of implementing continuous stochastic education in the school educational process were identified, ways of implementing continuous stochastic preparation of schoolchildren were offered, and examples of updating the content, methods, forms and means of learning the probability-statistical line were given. The conducted study has proved the effectiveness of formation of stochastic knowledge of schoolchildren in the system of continuous stochastic education. The materials of the article can be useful to teachers of mathematics, teachers of higher educational institutions, methodologists. |
RESUMEN: La relevancia de este estudio se debe al problema de la educación continua en las lecciones de matemáticas, necesidad de desarrollar nuevos métodos de enseñanza dentro de una de las líneas del curso escolar de las matemáticas-un estocástico, cuyo potencial es capaz de ejercer un significativo influir en la formación de la personalidad del alumno. El propósito del estudio es demostrar la necesidad de la realización de la educación estocástica continua en escuela. Métodos de investigación: experimento pedagógico (etapas de formación y control), un método de procesamiento estadístico de los resultados cuantitativos del estudio. Como resultado del estudio, se identificaron los problemas de la implementación de la educación estocástica continua en el proceso educativo de la escuela, se ofrecieron formas de implementar la preparación estocástica continua de los escolares, y ejemplos de actualización del el contenido, los métodos, las formas y los medios de aprender la línea probabilidad-estadística fueron dados. El estudio realizado ha demostrado la efectividad de la formación de conocimientos estocásticos de escolares en el sistema de educación estocástica continua. Los materiales del artículo pueden ser útiles para profesores de matemáticas, profesores de instituciones de enseñanza superior, metodológicos. |
At present, characterized as a period of post-industrial development in many countries of the world, almost every one of us receives an avalanche of information - through electronic media, publications, CDs, the Internet, and the media.
Qualification of a specialist from now on cannot be mediated only through the good performance of his work. Now it is not enough for a person of the future simply to graduate from a higher education institution - the younger generation needs to cope with the problem of continuing education, which is becoming more serious not only for budding specialist, but also for the schoolchildren themselves.
The problem of the continuous education of students in general academic school entails consideration and analysis of the sequence of different systems and levels of education, which go from purely theoretical to practical understanding. Thus, students have the right, even at school, to have free access to comprehensive education, to receive the necessary skills for their future profession in order to be able to fully realize the potential of a specialist in the future.
Obtaining and using information of all kinds, skillfully owning communication tools, analyzing complex situations, critically evaluating them and finding ways out of them, adequately changing the organization of their own activities, modern schoolchildren thereby demonstrate the ability to adapt to difficult living conditions. Surprisingly, the development of such abilities in school is facilitated by the study of mathematics, and, specifically, the study of one of its lines - stochastic, including elements of statistics, combinatorics and probability theory. In this regard, our task is to follow the continuity of the study of the stochastic line of the mathematics course in the Russian school, because the acuteness of this issue in the present situation is most palpable, since the stochastic component is introduced not only into middle and high school, but also into the junior one.
It is known that many researchers are concerned with the issue of continuing education. Some, for example, A.V. Darinskiy, H. Hummel, G. A. Yagodin and others, believe that the idea of continuing education exists as much as humanity itself. There is another point of view; its adherents (О.V. Kuptsov, V.G. Osipov and others) connect the emergence of the idea with the era of modernity, in which the active development of all spheres of human activity is constantly taking place. Adherents of the third point of view (A.P. Vladislavlev, G.P. Zinchenko, V.G. Onushkin and others) do not deny that the idea of continuing education has long existed in pedagogy, but they emphasize that the type of practice corresponding to this idea arose only in the Enlightenment.
Thanks to the terms used in foreign pedagogical literature, one can trace the genesis of the concept of "continuous education". So, for example, continuous education was designated as "continuous education" - "continuing education", "Lebensfange Bildung" - "lifelong education", "continuing education" - "continuing or extended education", "permanent education", “recurrent education", etc.
In addition, a number of approaches are known to the development of the theory of continuous education. So, in the works of the domestic researchers of the author's collective, edited by V.G. Onushkin continuous education is defined as a way and process. G.P. Zinchenko understands the idea under continuous education, A.P. Vladislavlev - activity. V.N. Turchenko and A.V. Darinskiy believes that continuing education is the principle of transforming and reforming the entire education system of the country, and B.S. Gershunskiy and A.V. Darinskiy believe that continuous education is a kind of system [5].
Also, continuous education in a systemic form represents the Concept of Continuing Education, drawn up on the basis of the results of study above the problem in question in 1989. The document indicated: "... the sense of continuity lies in the constant satisfaction of the developing needs of the individual and society in education, all-embracing in its completeness, individualized in time, pace, direction, in providing each with the opportunity to implement its own system of education" [5].
In their article, L.I. Maisenya & I.Yu. Matskevich [6] states that the rudiments of the idea of continuity in education originate in the 1950s. According to V.A. Klimenko [4], for the first time the formulation of the concept of "continuous education" was given in 1955 by the French scientist and educator P. Arentz, who puts forward the cultural and social aspects in the first place - preparing citizens for the existing conditions for the development of society and the dissemination of culture. At that time, the UNESCO Commission was at the origin of the idea of the continuity of education and defined the continuity of education as a system-forming principle. Over time, the principle of continuity of education was updated, it is necessary to pay tribute to R. Dave - Indian scientist, under whose influence this happened. R. Dave believed that continuous education is a phenomenon that continues throughout a person's life, striving for continuity, characterized by flexibility, a variety of content, means, forms and methods, having a relationship in the vertical dimension, integration - in the horizontal. At the same time, the opportunity, motivation and ability of the individual to receive education are the main prerequisites for continuity.
The methodological and theoretical foundations of the continuity of mathematical education find their place in the works of N.V. Argunova, M.S. Artyukhina, D.E. Davletova, L.N. Zhurbenko, R. Zaynieva, A.R. Latypova, A.G. Podstrigich, A.M. Popov, and Jeff Sanina, R.N. Huziakhmetova, A.E. Upshinskaya, Т.М. Churekova, E. V. Shemyakina and others.
A number of studies by Russian and foreign methodologists, including V.V. Afanasyev, E.A. Bunimovich, G.S. Evdokimova, D.V. Manevich, A. Plocki, T.A. Polyakova, V.D. Selyutin, Yu.N. Tyurin, V.V. Firsov, M.V. Shabanova, K. Bognar, M. Charles, A. Engel, M. Henry, M. Peltier, etc., is devoted to the development of questions of theory and methods of teaching elements of stochastics. For the most part, these scientific works are focused on the issue of staging of teaching statistics, combinatorics and probability theory in the general academic school, while the question of the continuity of the stochastic line of the school mathematics course in the mainstream of the ideas of the system-activity approach is still open.
Having studied the problems of the above question, and also having familiarized ourselves with a set of educational and methodological equipment for the subject study of stochastics, we formulate the definition of the continuity of the stochastic line of the school course of mathematics.
Under the continuity of the stochastic line of the school course of mathematics, we will understand the pedagogical system, which is an integral set of receptions, methods, means and forms for obtaining, deepening and expanding knowledge of students in the field of statistics, combinatorics and probability theory, as well as the process of climbing the educational potential of the schoolchild's personality in this field, which meets public needs and is provided by an educational institution.
Thus, the content of the concept of "continuity of the stochastic line of the school course of mathematics" includes the following important features:
Presence of subjects of the educational process at the lessons of mathematics - teachers and students;
Availability of a general content of textbooks for students of junior, middle and senior classes with a completed statistics line, combinatorics and probability theory, which will indicate the continuity of the presentation of the material;
The presence of a common view of the authors of textbooks on mathematics for schoolchildren of grades 1-11 on interpreting certain stochastic facts, on the relationship between "book" facts and real life;
The use of various methods, forms, receptions and means of instruction by the teacher for the aim of obtaining the maximum amount of knowledge of the stochastic line by the students as a result of the educational process;
Achievement of students with advanced or optimal level of stochastic culture as a result of continuous education.
The scope of the concept of "continuity of the stochastic line of the school course of mathematics" is presented by us in the form of a model-table for the continuous stochastic education of students of the general academic school, combining such component characteristics as: Achievement of students with advanced or optimal level of stochastic culture as a result of continuous education.
Such model is a special case of the model of continuous education, which was proposed by V.N. Turchenko [5]. In addition, the presented model will be universal in the study of most school subjects.
Let's denote the ways of realizing the continuity of the stochastic line of the school course of mathematics. First of all, this is implementation: all-embracing, integrity, continuity and individualization of the educational process in the lessons of mathematics.
Table 1. The Model of Continuous Stochastic Education Students of a General Academic School
|
Component view characteristics |
Component description characteristics |
1. |
Temporary |
The process of teaching schoolchildren the elements of stochastics in the general academic school. |
2. |
Spatial |
Unlimited space that is, learning (including self-study) stochastics can be carried out not only in school in class, but also outside school, at home. |
3. |
External |
Maximum convergence of stochastics with other school subjects, the implementation of intersubjective communications. |
4. |
Interior |
Continuity, closeness Elements of statistics, combinatorics and probability theory at all stages of education - junior, basic and middle. Mutual complement of various forms and types of training. |
5. |
Quantitative |
Stochastic education is received not only by students of the middle and high level, but also by the elementary (students of grades 1-11). |
6. |
Functional |
Each student, being a subject of self-education, is able to become an opponent to his teacher, in some cases even surpass the teacher. |
7. |
Development |
Continuous stochastic education involves updating the content, methods, forms and means of instruction, as a result of which the educational and cognitive process intensifies. |
The all-embracing educational process points to the unification of the common aim of junior, middle and senior schoolchildren to comprehend the deep knowledge of statistics, combinatorics and probability theory.
Integrity of the educational process in the conditions of continuity systematizes not only the activities of students and teachers in the lesson, but also the acquired knowledge, skills and skills of students, scientific facts and other theoretical knowledge into a single whole.
The continuity of the educational process is inseparable from the integrity, under which A.Kh. Shklyar understands the "gradual transition from one level of education to another," a consistent change in the "level of requirements for the volume and depth of mastering knowledge, skills," the organic "interconnection of content, basic methods and forms of teaching and educational process both at different levels of instruction, both and in different types of educational institutions "[6].
The individualization of the educational process consists in the teacher's individualized education of schoolchildren with skillful variation of the educational material, aims, methods and forms of instruction.
Note that with the realization of the continuity of the stochastic line of the school course of mathematics, a number of problems can arise, among which we distinguish: Social, psychological, organizational, pedagogical problems.
The social problem consists in building friendly relations between the teacher and schoolchildren of all age groups during the course and off-hour activities.
The psychological problem consists, first of all, in formation at schoolchildren of motivation to training stochastics, in development at them of cognitive requirements and interests to the given discipline. Important for the teacher is the identification of the peculiarities of the process of teaching the elements of statistics, combinatorics and probability theory in the general academic school.
The organizational problem is a problem, the solution of which provides for the trainees to follow a sequence of interrelated stages, among which: motivational-adaptive, theoretical-practical, reflexive-creative. Each stage is endowed with certain functions, depending on its aim and content. Thus, we classify the functions of the motivational-adaptive stage as axiological (it provides the formation of a value relationship and the organization of the process, taking into account the basic values of the schoolchild) and the adapting (ensures the student's adaptation to the stochastic material being studied). The functions of the theoretical and practical stage are the function of forming a stochastic culture (it determines the involvement of schoolchildren in the assimilation of the values of stochastic knowledge; by stochastic culture we mean the integral quality of the personality, the precondition and the condition of effective thinking activity in the field of stochastics, the generalized indicator of stochastic competence) and compensatory (replenishes the missing knowledge by using cognitive strategies). The leading functions of the reflexive creative stage are the creative (develops the creative potential of students in joint activity) and the regulatory (traces and corrects the process of forming a stochastic culture) function [9].
Pedagogical problems, from our point of view, are: The teacher determines the optimal content of the course of stochastics, aims, forms, methods, receptions and tools necessary to realize the continuity of the stochastic line. We add a number of requirements to the organization of the relationship and continuity of the elements of statistics, combinatorics and probability theory in the transition of students from junior to basic and from basic to middle education.
Subsequently, let us say that the teacher plays the leading role in the realization of continuous education. "It is difficult to overestimate the role of the teacher's personality, his spiritual appearance in the awakening and development of the aptitudes, inclinations, talents of the student..." [5]. Indeed, the schoolchild's knowledge system is determined by the teacher's knowledge system, and the ways of cognitive activity of the student are formed in accordance with similar ways of cognitive activity of the teacher.
To be more precise, in the 70-80s of the last century a number of dissertational studies on the possibilities of including statistics, combinatorics and probability theory in the school course of mathematics were substantiated. Scientists considered such aspects as: selection in the school course of mathematics through the content-methodological line, the joint study of combinatorics and statistics, the comprehension of combinatorics with the use of graphs, the development of various teaching methods for solving stochastic problems. Despite the fact that the above mentioned studies have focused on students of basic and middle schools, these scientific works have noted the feasibility of solving the problems of stochastics in primary classes. Thanks to this, according to many authors (L.S. Vygotsky, B.G. Heydman, V.V. Davydova, O.S. Medvedeva, A.G. Rubina, and A.P. Tonkikh); the foundations of conscious application of probability-statistical rules and formulas for students of middle school will be laid.
Relatively recently (in the 90s of the XX century), a new stage of studies have begun, connected with the entry of the statistics line, combinatorics and probability theory into the school course of mathematics. The stage is marked by the strengthening of the developing function of mathematical education and the emergence of scientific papers that reveal the role of probabilistic tasks in the development of schoolchildren's thinking. In connection with the creation of a system of continuous education, it becomes urgent to formulate and solve the problem of organizing continuity in the lessons of mathematics while studying the stochastic line between the junior and middle, middle and senior levels of the general academic school.
Table 2. Features of the presentation of the stochastic line in junior school
Subject lines of textbooks by a stochastic line |
M.I. Moro, S.V. Stepanova |
V.N. Rudnitskaya and others. |
T. E. Demidova, S.A. Kozlova, A.P. Tonkikh. |
L.G. Peterson |
G. V. Dorofeev T.N. Mirakova |
The main types of combinatorial problems |
|||||
1. Propaedeutics of the notion of graph |
|
1, 2, 4 classes |
2–4 classes |
|
2nd class |
2. Finding the number of permutations no more than from three elements |
|
2–4 classes |
2–4 classes |
2–4 classes |
|
3. The simplest tasks for the rule of the product (brute force solution) |
|
1–4 classes |
2–4 classes |
1–4 classes |
2, 4 classes |
4. Finding the number of combinations of 2 from three-five elements |
|
2–4 classes |
2–4 classes |
2–3 classes |
2nd class |
5. Problems on the propaedeutic of the concept "tree options» |
|
4th class |
4th class |
2-4 classes |
|
6. Placements without repetitions |
4th class |
|
|
|
2, 4 classes |
7. Stochastic Games |
4th class |
|
4th class |
|
|
Basic types of probability problems |
|||||
1. Finding the set of all outcomes of the experiment |
|
|
4th class |
|
|
2. Problems on the Dirichlet principle |
|
2–4 classes |
|
|
2nd class |
3. Introduction of the concepts of reliable, impossible and random events |
|
3–4 classes |
3d class |
|
|
4. Introduction of the concept of probability of an event with using the classical scheme |
|
|
4th class |
|
|
5. Calculation of probabilities of reliable, impossible, random events |
|
|
4th class |
|
|
Basic types of statistical tasks |
|
||||
1. Reading, interpreting, filling in tables |
1–4 classes |
|
2–4 classes |
1–4 classes |
1–4 classes |
2. Problems for the arithmetic middling |
4th class |
|
4th class |
|
|
3. Statistical studies |
1–4 classes |
|
3d class |
|
|
4. Reading the schedule, scheduling tasks |
|
4th class |
|
4th class |
|
5. Reading of linear and bar diagrams |
|
4th class |
4th class |
4th class |
|
6. Construction of simple linear and column diagrams according to the table |
|
|
4th class |
4th class |
|
7. Reading pie diagrams |
|
|
3 - 4 classes |
4th class |
|
8. Construction of pie diagrams |
|
|
|
4th class |
|
9. Introduction of the concept of random experiment, frequency of a random event |
|
|
3 - 4 classes |
|
|
10. Calculation of the frequency of an event in a series of identical random experiments |
|
|
4th class |
|
|
We carry out comparative-relative analysis of textbooks and manuals on stochastics, consistently analyzing book editions for junior, middle and senior level.
I.O. Kovpak [3] in his work analyzes the meaningful filling of the stochastic line of mathematics in junior school (see Table 2) and says that the proposed textbooks on mathematics in sufficient volume represent the statistical component of the stochastic line. Despite this fact, notes that only two authors of the collective "School 2100" and "Junior School of the 21st Century" fully implement uniform, consistent and continuous training.
Indeed, this table shows completely different approaches to the study of stochastics, most of them are inconsistent and uneven. From our point of view, when teaching statistics, combinatorics and probability theory to middle school schoolchildren, the teacher may have some difficulties, the reasons for which will be the lack of proper continuity or the fragmented content of the textbooks. This will happen due to different starting levels of training for students who have completed junior school.
Let's now turn to the textbooks for middle and senior students. Let's follow the structure of each of them.
Textbook |
Structure |
|
1. |
Textbook A.G. Mordkovich and P.V. Semenov (7-9 classes), [8]. |
The simplest combinatorial problems. The rule of multiplication and the tree of options. Permutations. Selection of several options. Combinations. Random events and their probabilities. Statistics - design information. Independent repeat tests with two outcomes. |
2. |
Textbook Yu.N. Makarychev and N.G. Mindyuk edited by S.A. Telyakovskogo (7-9 classes) [7]. |
Statistical characteristics. Statistical studies Elements of combinatorics. Initial information from the theory of probability. |
3. |
Textbook M.V. Tkachyova and N.E. Fedorova (7-9 classes) [11]. |
Introduction to combinatorics. Random events. Random variables. |
4. |
Textbook Yu.N. Tyurin, A.A. Makarov, I.R. Vysotsky, I.V. Yaschenko (7-9 classes) includes thirteen chapters [12].
|
Tables. Diagrams. Descriptive statistics. Random variability. Random events and probability. Mathematical description of random phenomena. Probabilities of random events. Addition and multiplication of probabilities. Elements of combinatorics. Geometric probability. Tests of Bernoulli. Random variables. Numerical characteristics of random variables. Random variables in statistics. |
5. |
A Handbook for general academic institutions Е.А. Bunimovich and V.A. Bulychev (5-11 classes) [2]. |
Random events. Probabilistic scale. Tables and diagrams. Random experiments and the frequency of events. Statistical definition of probability. The classical definition of probability. Once again about the outcomes and events. Random sampling and its representation. Statistical characteristics of the middle. Statistical characteristics of the scatter. Probability and combinatorics. Random numbers and computer. Geometrical definition of probability. Statistical estimation and forecast. Statistical studies Axiomatic definition of probability. |
6. |
Textbook Yu.N. Tyurin, A.A. Makarov, I.R. Vysotsky, I.V. Yaschenko (10-11 classes) contains fourteen chapters [12].
|
Random events and probability (repetition of basic concepts). Mathematical description of events. Conditional probability. Random variables and distributions. Several random variables. Independent random variables. Geometric distribution. Combinatorics. Bernoulli tests and binomial distribution. Law of large numbers. Continuous random variables. Normal distribution. Exponential distribution. Linear regression and selective correlation coefficient. |
The structure of the teaching aids indicates the need to re-pass the material already studied. So, for example, a textbook developed by the author's collective Yu.N. Tyurin (10-11 classes) begins with the chapter "Random events and probability (repetition of basic concepts). The title of the same title is the fifth chapter of the manual on stochastics for 7-9 classes of the same author's line. In this illustrative example, it is easy to convince oneself of the question of duplicating theoretical material, which gradually grows into a global methodological problem. From our point of view, a re-study of what has already been mastered hinders the personal development of schoolchildren, and the educational motivation falls.
In addition, the authors of each manual dispose of the training material in such a way that it turns out to be subordinate to the repetition of what was studied earlier in the junior or basic school, in some cases the presentation of the stochastic line begins with "zero". There is a violation of such ways of realizing the continuity of the stochastic line, as integrity and continuity in the system "junior general - basic general - middle general education".
In the textbooks E.A. Bunimovich & V.A. Bulychev [2], Yu.N. Makarychev & N.G. Mindyuk [7], A.G. Mordkovich & P.V. Semenov [8], M.V. Tkachevoi & N.E. Fedorova [11], Yu.N. Tyurin, et.al. [13], Yu.N. Tyurin, et.al [12] there is no unified view on the presentation of theoretical material, there is no general content, and the presented information is divorced from real life. At the same time, they trace the incompleteness of the stochastic line, indicating the lack of continuity in the presentation of the material.
The methodical study of the stochastic line of the school course of mathematics with the aim of adapting it to the age-specific features of the students' thinking should adhere to a consistent and systematic study of the theoretical foundations of the subject. The entire period of studying stochastics should be accompanied by the expansion, deepening and consolidation of the knowledge, skills and abilities that were obtained by schoolchildren at the previous stage of educational activity. The effectiveness of training students in the formation of stochastic representations will be achieved in the case of general theoretical grounds of this discipline in the system of continuous mathematical education.
It is easy to check whether the educational process was effective at the lessons of mathematics in the system of continuous education.
Achieving the maximum amount of knowledge of the stochastic line at the moment of control under continuous education will be described by a mathematical model of a general form proposed by A.A. Beznosyuk [1].
Let's, for simplicity, knowledge and skills (KAS or compressed-knowledge) from the stochastic line of the school course mathematics be absorbed by the schoolchildren at a constant rate V0. Accumulated KAS are forgotten at a rate that is proportional to their volume (X-volume). In this case, the proportionality coefficient will be assumed constant. As well as the rate of assimilation of KAS, it depends on the individual characteristics of the student and on the specifics of the educational material. Denote it ![]() , here
, here ![]() is the characteristic time of forgetting.
is the characteristic time of forgetting.
The process of changing the volume of heaped-up KAS of a stochastic line is represented as a linear differential equation:
![]() .
.
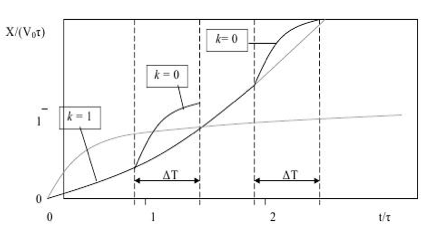
We reflect the features that are inherent in innovative learning technologies.
We introduce the value Y - the volume of "innovative" (acquired in the process of continuous study of the stochastic line) KAS schoolchildren. We will assume that the rate of growth of knowledge from the stochastic line of the school course of mathematics, obtained independently by the student, is proportional to the volume of "innovative" knowledge. For the frequency of mastering "innovative" knowledge, we take the coefficient f, which, like the coefficient ![]() , will be constant.
, will be constant.
Let the total rate of formation of "traditional" and "innovative" knowledge of statistics, combinatorics and probability theory be equal V0. Modern teaching technologies can differ from each other in the ratio of the efforts of the teacher and schoolchild which are also spent on the formation of "traditional" and "innovative" knowledge. For the speed of the formation of "traditional" knowledge we will accept![]() , for the speed of the formation of "innovative" knowledge
, for the speed of the formation of "innovative" knowledge![]() .
.
The intensity of forgetting "innovative" knowledge is not observed because the student constantly uses them as a tool for self-education. As a result, the coefficient of proportionality will be equal to zero.
The above described processes of changing the volumes of piled up "innovative" and "traditional" knowledge of stochastics are united and presented in the form of a system of differential equations:

Thus, the teacher only needs to offer a function that can predict optimal strategies to achieve the maximum amount of knowledge of the stochastic line, and the maximization strategy itself is already known.
Fig. 1 Dependence of the volume of "traditional" knowledge of stochastics on time
for technologies that differ in part of the efforts aimed at the formation
of "innovative" stochastic knowledge
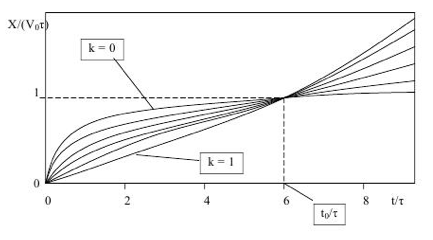
Continuous education has become one of the global problems of our time. Many scientists and even only ascendant scientists are engaged in the formulation and solution of certain issues of this problem. The educational process of general academic institutions - schools, which should be built on each of the lessons within the framework of the continuous system - is not left without attention. The lessons of mathematics are no exception, so in the article we tried to point out the possible ways of realizing the continuous learning of one of the lines of the school course of mathematics - probabilistic-statistical. In the course of the study, the optimal strategies for achieving the maximum amount of knowledge of the stochastic line at the time of monitoring under continuous education were reflected.
During the study, the problem of ensuring the continuity of the stochastic line of the school course of mathematics in the mainstream of the ideas of the system-activity approach was solved. In the course of solving this problem, it was established that the continuity of the stochastic line in textbooks and teaching aids is almost not observed. Therefore, we proposed methodological recommendations for the implementation of the continuity of the course of mathematics (stochastics), as well as the scope and content of the concept of "continuity of the stochastic line of the school course of mathematics".
The study was carried out with the financial support of the Russian Foundation for Fundamental Research (Department of Humanities and Social Sciences). Project 17-36-01004 "Theoretical and methodological foundations for the realization of continuity and continuity in the development of the stochastic line of the school course of mathematics in the mainstream of the ideas of the system-activity approach".
1. Bunin Yelets State University. Institute of Mathematics, Natural Sciences and Technology. Yelets, Russia. email: scherbatych2017@yandex.ru
2. Bunin Yelets State University. Institute of Mathematics, Natural Sciences and Technology. Yelets, Russia