ISSN 0798 1015

Vol. 38 (Nº 26) Año 2017. Pág. 9

Eficiência técnica de pequenos produtores de soja da região de Dourados (MS)

Technical efficiency of small soy farmers in region of Dourados (MS)

Celso Correia de SOUZA 1; Fabio Antonio SILVA 2; Gustavo Anderson Gimenes DEBOLETO 3; Leonardo Marinho de CARVALHO 4; José Francisco dos Reis NETO 5; Daniel Massen FRAINER 6; Luiz Henrique Brito LEMES 7

Recibido: 13/12/16 • Aprobado: 25/01/2017

Conteúdo

1. Introdução

2. Fundamentação teórica

3. Material e métodos

4. Resultados e discussões

5. Conclusões

Referências bibliográficas

1. Introdução

Atualmente, o Brasil ocupa notável posição mundial no agronegócio, com grandes perspectivas para o futuro em face de suas características e diversidades, tanto de clima quanto de solo, possuindo ainda áreas agricultáveis altamente férteis e ainda inexploradas. Com o aumento da população mundial e sua consequente demanda por alimentos, leva a uma previsão de que o Brasil alcançará o patamar de líder mundial no fornecimento de alimentos e commodities ligadas ao agronegócio, solidificando sua economia e implementando o seu crescimento (MDIC, 2015).

O Agronegócio tem uma expressiva participação na economia do Brasil, e representa aproximadamente 22 a 23% do PIB brasileiro, com cerca de R$ 1,178 trilhões de reais em 2014, crescendo em torno de 1,6% em relação a 2013. Em torno de 68% desse crescimento refere-se ao segmento da agricultura, e somente a soja é responsável por mais de 31% deste valor. Tais resultados colocam o Brasil como segundo maior produtor da oleaginosa, atrás apenas dos Estados Unidos, contabilizando a produção de 86,12 milhões de toneladas em uma área de 30,10 milhões de hectares de plantio de soja. A produtividade média da soja no país é de 2.842 kg/ha (MAPA, 2014).

O Estado do Mato Grosso do Sul (MS) é o 5º maior produtor de soja do Brasil, responsável por cerca de 6,14 milhões de toneladas (safra 2013/14) em, aproximadamente, 2,12 milhões de hectares plantados, e tem no agronegócio o principal pilar da sua economia. O estado do MS destaca-se também na produção de carne, milho, cana de açúcar, entre outros (CONAB, 2014).

Estudos e pesquisas sobre o cultivo da soja dá o tom da sua importância no agronegócio brasileiro, com novas variedades, novas formas de plantio, novas tecnologias de cultivo e a avaliação técnica no que se refere à sua eficiência de produção, pois, o antigo produtor de soja é hoje qualificado como empresário rural, que precisa mensurar da melhor forma possível a utilização dos recursos, que são limitados, para obter uma melhor rentabilidade para se manter neste mercado altamente competitivo.

O produtor precisa estar atento ao seu nível de eficiência, que seria a utilização consciente dos seus insumos como: mão de obra, fertilizantes, corretivos, sementes, agrotóxicos e maquinários, entre outros, uma vez que o produto final é uma commodity que tem o preço pré-determinado pelo mercado, não havendo margem de negociação na venda, portanto, só restando ao produtor a redução nos custos de produção como opção na concorrência. O mercado da soja é classificado como oligopsônio, em que existem muitos produtores querendo vender suas safras para um número reduzido de compradores do produto. Por outro lado, existe mais um agravante, que é o número reduzido de fornecedores de insumos, caracterizando, também, um oligopólio. Desse modo, tanto “antes da porteira” quanto “depois da porteira” não se tem muitas opções. 

O produtor rural ainda precisa estar atento às variáveis climáticas, sol, chuva, temperatura, umidade, pois, existem dificuldades de se prever com antecedência essas ocorrências externas, para que se tenha tempo hábil de tomar as medidas necessárias com intuito de minimizar os impactos negativos, assim, o produtor tem controle sobre poucas variáveis, a principal é a melhor utilização dos recursos de produção. Para isso é preciso mensurar o seu desempenho através dos resultados que pode indicar se está no caminho certo ora trilhado, ou o que precisa ser reformulado.

Deste modo, faz-se necessário a mensuração do grau de eficiência do produtor rural, principalmente do pequeno produtor que não dispõe de meios adequados para essa mensuração. Recentemente, com os avanços da tecnologia de informação, criou-se uma ferramenta gerencial denominada de Análise Envoltória de Dados (DEA), que se baseia em programação matemática, sendo um procedimento não paramétrico, com o objetivo de avaliar comparativamente, e relativamente, eficiências de unidades tomadoras de decisão (Decision Making Units - DMU), aqui representadas pelos pequenos produtores rurais envolvidos na pesquisa.

 O objetivo geral deste trabalho foi analisar as eficiências de pequenos produtores de soja da região da Grande Dourados utilizando a técnica de Análise Envoltória de Dados (DEA). Para facilitar a consecução do objetivo geral proposto, propõem-se ainda como objetivos específicos: classificar em unidades produtivas eficientes e ineficientes os produtores de soja e determinar os produtores eficientes que servirão de espelhos (benchmarking) para os produtores ineficientes, a fim de que se tornem eficientes; determinar os excessos ou as limitações no uso de insumos que dificultam as unidades ineficientes a tornarem-se eficientes. 

2. Fundamentação teórica

A Análise Envoltória de Dados (DEA) teve início em 1978, com o objetivo de comparar a eficiência de escolas públicas norte-americanas levando-se em conta: escores aritméticos; medidas da autoestima em testes psicológicos; habilidades psicomotoras de alunos; número de horas-aulas dos professores e; tempo gasto pela mãe em leituras com o filho. Atualmente, esta técnica é empregada em diversos problemas das ciências, inclusive, àqueles de cunho empresarial (LINS & MEZA, 2000).

A DEA é uma técnica não paramétrica de Programação Linear, ligada à Pesquisa Operacional, que permite analisar comparativamente unidades independentes (empresas, departamentos, assentamentos, etc.) no que se refere ao seu desempenho operacional. Ela fornece uma medida para avaliar a eficiência técnica relativa das unidades de tomada de decisão (Decison Making Unit - DMUs). As DMUs podem ser departamentos ou divisões de uma empresa, unidades administrativas ou operacionais, redes de empresas e suas filiais, produtores rurais de determinada cultura, ou seja, essa técnica é adaptável a qualquer problema que tenha como objetivo a análise de eficiência comparada (alocativa) (PEREIRA, 1995).

 Segundo Pereira (1995) e Azambuja (2002), a eficiência se apresenta de duas formas: eficiência técnica e eficiência alocativa. No caso, a eficiência técnica mede a proximidade entre a quantidade de produtos que uma DMU produz e a quantidade máxima de produtos que essa DMU poderia produzir, dado o nível de insumos que pratica. O conceito de Pareto-Kolmman para a eficiência é caracterizado por um vetor input-output, de modo que uma DMU é eficiente se e somente se: nenhum output possa ser aumentado sem que algum input seja aumentado, ou algum outro output seja reduzido; nenhum input possa ser reduzido sem que outro input seja aumentado, ou algum output seja reduzido.

A pressuposição fundamental na técnica DEA é que, se uma dada DMU “A” é capaz de produzir Y (A) unidades de produto, utilizando X(A) unidades de insumos, então outras DMUs poderiam também fazer o mesmo, caso elas estejam operando eficientemente. De forma similar, se uma DMU “B” é capaz e produzir Y(B) unidades de produto, utilizando X(B) de insumos, então outras DMUs seriam capazes de realizar o mesmo esquema de produção.   

Existem em DEA dois modelos básicos para se encontrar a eficiência técnica de uma DMU: modelos CCR (Retornos Constantes de Escala) e BCC (Retornos Variáveis de Escala). O primeiro pressupõe o retorno constante de escala, isto é, uma variação nos inputs implicará uma variação nos outputs, de forma proporcional; o segundo pressupõe que uma variação nos inputs implicará uma variação não proporcional nos outputs (CHARNES et al., 1978; BIONDI NETO, 2001). 

No uso da DEA, deve-se fazer uma opção: usar um modelo orientado a outputs, no qual se obtém o máximo nível de outputs mantendo os inputs fixos, ou um modelo orientado a inputs, que visa a obter um menor uso de inputs dado o nível dos outputs. A decisão de usar um ou outro modelo deve ser previamente selecionada pelo pesquisador. 

O modelo CCR

Nesse modelo define-se a eficiência como a razão entre a soma ponderada dos outputs pela soma ponderada dos inputs. O modelo permite que sejam atribuídos tanto aos inputs quanto aos outputs um conjunto de pesos para cada DMU, no sentido de maximizar a sua eficiência. Neste caso, a função (ou fronteira) de produção corresponde a uma reta que passa pela origem de um sistema cartesiano, em que o eixo horizontal representa os insumos e o vertical, produtos. Se o desempenho da DMU está sobre a fronteira de eficiência, ela é tida como tecnicamente eficiente, caso contrário, se o seu desempenho está abaixo da fronteira, a empresa é tida como tecnicamente ineficiente. A única condição é que todas as DMUs tenham uma eficiência menor ou igual a 1 (AZAMBUJA, 2002).

A formulação matemática dessas condições, denominadas de programação matemática, são apresentadas pelas equações 1 e 2.

Esses dois modelos têm infinitas soluções, e fazem parte de um problema de programação fracionária. Eles podem ser transformados em problemas de programação linear (PPL), cada um com uma única solução, fazendo o denominador da função objetivo igual a uma constante que, por conveniência, normalmente é igual a 1. Com essa simplificação os modelos tomam as formas apresentadas nas equações 3 e 4, denominadas de modelos primais (CASADO, 2007; CASADO & SILUK, 2011).

Os modelos de minimização de inputs buscam a minimização de insumos mantendo, no mínimo, o nível de produção atual, expresso pela maximização do somatório, com a soma ponderada dos insumos no denominador. Os modelos duais buscam os valores de que minimizem , com  a contribuição da DMUk na formação do alvo (objetivo) da DMU0, portanto, os benchmarks da DMU0 (CASADO, 2007; CASADO & SILUK, 2011).

As representações gráficas desses dois modelos estão nas Figuras 1 e 2.

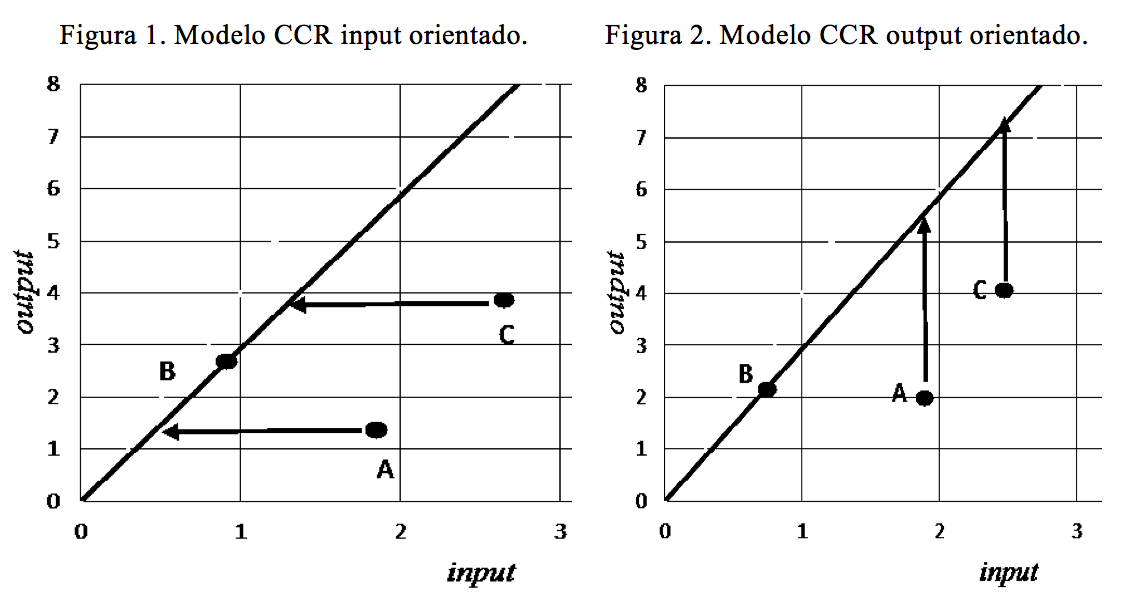
Estudo semelhante poderia ser feito para o modelo BCC, não sendo feito, pois, não foi objeto desse estudo, que se optou pelo método CCR input orientado. Os níveis de eficiência variam de 0 a 1, quanto mais próximo de 1, melhor é o nível de eficiência. Será considerada eficiente aquela DMU com nível de eficiência igual a 1. No Quadro 1 estão discriminados os níveis de eficiência para as DMUs em análises (OLIVEIRa, 2012).

 Quadro 1. Níveis de eficiências.

Fonte: Adaptado de Oliveira et al. (2012).

A determinação de benchmarks é uma das características gerenciais mais importantes dos modelos DEA clássicos. Na Figura 3 é apresentado um modelo DEA com dois inputs e um output, sete DMUs, A, B, C, D, E, F e G.

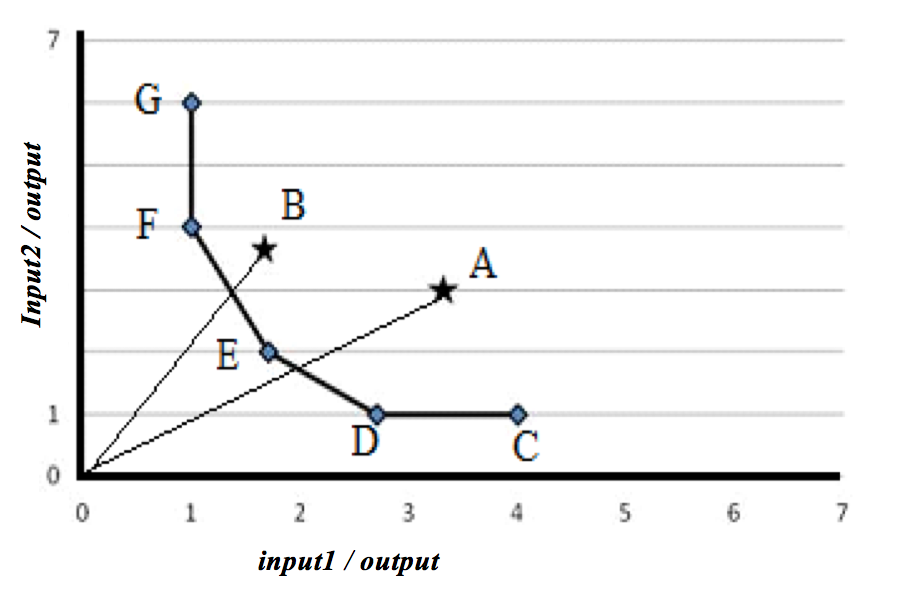
Figura 3. DMUs eficientes e não eficientesde um problema envolvendo a DEA.
Fonte: Ferreira e Gomes (2012).

Das sete DMUs da figura, são eficientes  C, D, E, F e G, pois, estão sobre a fronteira de eficiência e, como ineficientes, as DMUs A e B, que não estão sobre essa fronteira. As retas que ligam as DMUs ineficientes A e B à origem permitem encontrar os alvos dessas DMUs, que são os pontos onde as retas interceptam a fronteira de eficiência. Por exemplo, para a DMU A, o alvo encontra-se no segmento de reta determinado pelas DMUs  E e D, que são os seus benchmarks. Como a interseção está mais próxima da DMU E do que da DMU D, a DMU E é um benchmark mais importante para a DMU A. Análise semelhante pode ser feita para a DMU B.

Essa mesma análise também pode ser feita algebricamente pelo cálculo dos pesos λ’s (equações 6 e 7). Se λ for igual a zero, significa que a DMU correspondente não é benchmark para a DMU em análise. A importância da DMU correspondente aumenta em relação à DMU ineficiente em análise quando aumenta o valor de λ. No exemplo da Figura 3, para a DMU A, os pesos λB, λC, λF e λG são iguais a zero.

As metas são os valores dos alvos a serem atingidos pelas referidas DMUs, de modo a alcançar um nível de eficiência ótimo e as folgas são caracterizadas como sendo a diferença do valor da DMU atual para o valor do alvo dessa DMU. A forma clássica de determinar alvos em DEA considera a possibilidade de orientação a inputs ou a outputs. Essas orientações consideram que a DMU atinge a fronteira eficiente mantendo os inputs constantes e aumentando os outputs, ou congelando os outputs com a diminuição dos inputs.

Para as DMUs C, D e E, só é possível reduzir um input e permanecer na região eficiente de produção aumentando o outro input e vice-versa, ou reduzindo o seu output. Essas três DMUs sãso denominadas de ótimos de Pareto. Já as DMUs F e G, apesar de eficientes, têm comportamentos diferentes das demais, pois, no caso da DMU F, pode-se diminuir o Input 1 mantendo constante o Input 2 que ela permanecerá na região eficiente de produção. Fato semelhante ocorre com a DMU G.

As quantidades (inputs) que ainda são possíveis serem reduzidas são conhecidas como folgas. Observa-se, assim, que apesar de serem 100% eficiente, as DMUs F e G não são tão eficientes quanto as outras unidades eficientes. Assim, diz-se que a DMU F é dominada pela DMU C e que a DMU G é dominada pela DMU F. Para um modelo DEA CCR orientado a inputs, por exemplo, o valor da folga será igual a zero quando as restrições do modelo (5) forem iguais a zero para h0 e λk ótimos.

3. Material e métodos

O objeto da pesquisa foram os pequenos produtores de soja, num total de 48, assistidos pela Agência de Desenvolvimento Agrário e Extensão (AGRAER/MS), da região da Grande Dourados e que possuem até dois módulos fiscais. A região da Grande Dourados é composta por 12 municípios: Caarapó, Deodápolis, Douradina, Dourados, Fátima do Sul, Glória de Dourados, Itaporã, Jateí, Nova Alvorada do Sul, Rio Brilhante, Vicentina e Juti, com uma área total de 21.329,50 km² (MDA, 2013).

O estudo da medida de eficiência técnica usando a DEA foi dividido em três fases principais: seleção das DMUspara a análise; determinação dos insumos (inputs) e produtos (outputs) relevantes para avaliar a eficiência técnica relativa das DMUsselecionadas e; criação e solução do modelo DEA e análises dos resultados (ROLL et al., 1991). Neste trabalho foram utilizadas oito variáveis que impactam diretamente na questão econômica das pequenas propriedades rurais, num total de 48. Portanto, 48 DMUs, atendendo condições impostas para a aplicação da teoria.

Para a coleta de dados das oito variáveis: área de plantio de soja (ha), gastos (em R$) com fertilizantes, sementes, agrotóxicos, aluguel de maquinários e mão de obra, desde o plantio até a colheita e que serviram como inputs e, como outputs, as variáveis produtividade (kg/ha) e lucratividade (receita bruta total/ despesa operacional total).

Algumas condições devem ser impostas para a implementação de um modelo DEA: 1) Seleção rigorosa das DMUs a entrarem na análise, lembrando que uma vez definidas as DMUs, estas devem ser no mínimo o dobro do número de variáveis utilizadas no modelo; 2) Seleção das variáveis (input e output), considerando, a princípio, uma grande lista de possíveis variáveis a entrar no modelo, estas variáveis quantitativas ou qualitativas. A introdução de um grande número de variáveis reduz a capacidade do DEA de distinguir as DMUs eficientes das ineficientes e, portanto, o modelo deve ser o mais compacto possível para maximizar o poder discriminatório do DEA e; 3) A escolha do modelo a ser aplicado e a orientação a input ou output levando-se em conta: o número de inputs e outputs, isto é, em havendo muito mais inputs do que outputs, altos valores dos insumos, escassez dos insumos, etc., o modelo deve ser orientado a input, caso contrário, output (MELLO et al., 2005).     

Neste estudo foi utilizado o modelo DEA- CCR, input orientado, pois, de acordo com a leitura do modelo, o CCR pressupõe um retorno constante de escala, existindo uma relação linear entre inputs e outputs eos insumos têm altos valores agregados. Deste modo, com as escolhas feitas das variáveis de insumos (inputs) e produtos (outputs), um incremento ou uma redução de insumogerava um incremento ou uma redução proporcional de produtos. Ademais, a orientação insumo foi devido à decisão de se diminuir o consumo de insumos sem alterar a produção, conforme objetivo do trabalho, pois, os insumos usados neste trabalho são escassos e onerosos, devendo ser minimizados.

Utilizou-se neste trabalho o software “Sistema de Apoio à Decisão – SIAD V3.0”, para a análise da eficiência dos pequenos produtores de soja da região da Grande Dourados (UFF, 2015).

4. Resultados e discussões

Os dados coletados na pesquisa de campo, Anexo A, foram inseridos no software SIAD e modelo CCR input orientado devido ao maior número de variáveis de entrada (inputs), e o alto custo dos mesmos, podendo ser considerados bens escassos. Na Tabela 1 são apresentados os resultados obtidos através do processamento do SIAD que, de acordo com o Quadro 1, apresenta as escalas de eficiências, destacando-se as DMUs 8 e 14 como sendo eficientes na utilização dos recursos.

Tabela 1. Resultados do processamento SIAD – CCR input orientado e os níveis de eficiências equivalentes de cada DMU na produção de soja.

Além de identificar as DMUs eficientes, o modelo DEA permitiu medir e localizar a ineficiência e fornecer os benchmarks para as DMUs ineficientes. Esses benchmarks são determinados pelas projeções das DMUs ineficientes na fronteira de eficiência (GOMES et al., 2003).

A DEA apontou as DMUs 08 e 14 como eficientes, as restantes são ineficientes, porém, cada uma delas apresenta um grau diferente de ineficiência. Na Tabela 2 estão apresentados os pesos encontrados no modelo pelo software SIAD, que representam os pesos relativos associados a cada unidade eficiente no cálculo da taxa de eficiência para as unidades ineficientes.

Tabela 2. Pesos relativos associados a cada DMU eficiente no cálculo da taxa de eficiência para as DMUs ineficientes.

Na análise dos resultados da Tabela 2 pode-se ter uma visão das DMUs ineficientes, e como elas podem utilizar as DMUs eficientes como referência para se tornarem eficientes. Como, por exemplo, a DMU 1, que é ineficiente, tem como benchmarkings (referências) as DMUS 8 e 14, utilizando de 11,27% da DMU 8 e 88,73% da DMU 14 para se tornar eficiente. Portanto a DMU 14 é um benchmarking mais importante para a DMU1. Análises semelhantes poderiam ser feitas para as outras DMUs ineficientes.

Na Tabela 3 estão apresentados os resultados obtidos pelo software SIAD: valor atual, radial, folga e alvo das variáveis envolvidas no problema que tornam, por exemplo, a DMU 1 (eficiência = 0,421692), tendo como benckmarks as DMUs 8 e 14 eficientes, inclusive, os níveis (folgas) que as variáveis devem atingir para que a DMU 1, ineficiente, alcance a fronteira de eficiência.  

Tabela 3. Valores encontrados pelo SIAD: atual, radial, folga e alvo das variáveis da DMU 1 (eficiência = 0,421692),
que a torna eficiente, utilizando as DMUs 8 e 14 como benchmarks.

Uma análise dos parâmetros da Tabela 3 permite concluir que: na coluna “Atual” estão os níveis de valores iniciais das variáveis da DMU 1; na coluna “Radial = eficiência DMU 1× Atual”, estão os níveis de valores das variáveis que utilizados no processo da cultura da soja; a coluna “Folga = Radial - Alvo”, representa a diferença do valor Radial para o valor do Alvo e; a coluna “Alvo = peso DMU 8×Atual+peso DMU 14×Atual”, estão os níveis de valores das variáveis da DMU 1 que deveriam ser assumidos pela mesma, tendo como referências as DMUs 8 e 14, para chegar à eficiência.

Analisando a primeira linha da Tabela 3 (Área de plantio), tem-se: Atual (inicial), 10ha; Radial = 0,421692×10 = 4,21692; Folga = 4,21692 – 4,21692 = 0 e; Alvo = 0,11281×4,5 + 0,88316×4,2 = 4,21692. Desse modo, o produtor 1 (DMU 1) está trabalhando com folga em cinco insumos, isto é, está utilizando tais insumos em excesso, com desperdícios (fertilizante em R$1,57, sementes em R$1,02, agrotóxicos em R$0,07, mão de obra em R$0,40 e aluguéis maquinários R$1,06. Só não existe folga em área de plantio, com folga zero.

Os valores obtidos da Tabela 3 são pequenos, mas no conjunto de todas as variáveis, o produtor 1 (DMU 1) está deixando de produzir 100 kg/ha.  Em uma lavoura de grande porte o produtor estaria deixando de ganhar uma alta quantia, que deve ser levada em conta. Análises semelhantes poderiam ser feitas para todas as DMUs ineficientes, cujos resultados estão nas saídas do software SIAD V3.0.

5. Conclusões

Com o uso da ferramenta DEA, é possível aos produtores e aos técnicos da AGRAER obterem mensurações mais aprofundadas do desempenho individual de cada produtor, avaliarem os que estão operando em plena eficiência, como também, aqueles que têm altos desempenhos, mas ainda não são eficientes.

O método utilizado possibilita a comparação em um sentido multidimensional, nas mais diversas unidades de medidas, e mostra a capacidade com que cada DMU transforma seus insumos em produtos, e ainda, informa alterações que devem ser realizadas no nível de utilização de insumos e de produtos para tornar as DMU’s ineficientes em eficientes. A correção das ineficiências dos pequenos produtores de soja da região da Grande Dourados aumentará o potencial produtivo dos mesmos, permitindo um melhor desempenho econômico por parte de cada produtor, fazendo que ele alcance a plena sustentabilidade econômica.  

A técnica DEA, para a quantificação da eficiência técnica, é muito útil ao estado de Mato Grosso do Sul e ao Brasil, pois, existe uma carência muito grande de instrumentos deste porte e neste campo, para auxílio à gerência nos processos decisórios.

Apesar de não ser de difícil aplicação, a metodologia da DEA exige alguns cuidados, principalmente, na escolha das variáveis que farão parte do problema, aquelas variáveis que serão os insumos (inputs) e aquelas que serão produtos (outputs), na escolha do modelo apropriado, bem como, ser cuidadoso com a utilização do banco de dados.

Tendo em vista as oportunidades de melhoria através do software DEA-SIAD, sugere-se a AGRAER que o adquira e promova cursos junto aos técnicos para difundir essa metodologia de pesquisa.

Agradecimento: Agradecemos à Fundação Nacional de Desenvolvimento de Ensino Superior Particular - FUNADESP pelo apoio financeiro

Referências bibliográficas

ANGULO MEZA, L.; MELLO, J. C. C. B. S.; GOMES, E. G;  MELLO, M. H. C. S. Uma análise da qualidade e produtividade de programas de pós-graduação em Engenharia, Relatórios de Pesquisa em Engenharia de Produção. Niterói: Universidade Federal Fluminense, 2001.

AZAMBUJA, A. M. V. Análise de Eficiência na Gestão do Transporte Urbano por Ônibus em Municípios Brasileiros. 2002. 385 f. Tese (Doutorado em Engenharia de Produção) – Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis.

BIONDI NETO, L. N. DEA: Nova Metodologia para Determinação da Eficiência Relativa de Unidades Tomadoras de Decisão. Rio de Janeiro, 2001. Tese (Doutorado em Engenharia de Produção) – Engenharia de Produção, Universidade Federal do Rio de Janeiro.

CASADO, F. L. Análise Envoltória de Dados: conceitos, metodologia e estudo da arte na Educação Superior. SOCIAIS E HUMANAS, SANTA MARIA, v. 20, n. 01, jan/jun 2007, 59-71.

CASADO, F. L.; SILUK, J. C. M. Avaliação da Eficiência Técnica de Instituições Públicas Através da Utilização de Indicadores de Governança. XXXI Encontro Nacional de Engenharia de Produção. Belo Horizonte, MG, Brasil, 04 a 07 de outubro de 2011.

 CHARNES, A; COOPER, W. W; RHODES, E. Measuring the efficiency of decision making units. European Journal of Operational Research, Austin, v. 2, p. 429-444, 1978.

CONAB. Levantamento Safra 2013/14. Disponível em http://www.conab.gov.br/OlalaCMS/uploads/arquivos/14_09_10_14_35_09_boletim_graos_setembro_2014.pdf. Acesso em 25/09/2014.

GOMES, E. G.; LINS, M. P. E.; ANGULO MEZA, L.; SERAPIÃO, B. P.; MELLO, J. C. B. S.; ANTUNES, J. S. Análise de envoltória de dados no estudo da eficiência e dos benchmarks para companhias aéreas brasileiras. Pesquisa Operacional, Rio de Janeiro, v. 23, n. 2, p. 325-345, 2003.

LINS, M. P. E.; ANGULO MEZA, L. Análise Envoltória de Dados e perspectivas de integração no ambiente de apoio à decisão. Rio de Janeiro: COPPE/UFRJ, 2000.

LINS, M. P. E.; MOREIRA, M. C. B. Método I: O stepwise para seleção de variáveis em modelos de Análise Envoltória de Dados. Pesquisa Operacional, Rio de Janeiro, v. 19, n. 1, p. 39-50, 1999.

MAPA – Ministério da Agricultura, Pecuária e Abastecimento. Produto Interno Bruto da agropecuária deve ser de R$ 1,1 trilhão. Disponível em http://www.agricultura.gov.br/comunicacao/noticias/2014/12/produto-interno-bruto-da-agropecuaria-deve-ser-de-rs-1-trilhao acesso em 23/01/2015.

MDIC – Ministério da Indústria, Comércio Exterior e Serviços. Balança comercial brasileira. Disponível em <http://www.desenvolvimento.gov.br//sitio/interna/interna.php?area=5&menu=4861&refr=1161>. Acesso em 25/01/2015.

OLIVEIRA, R. D. Análise da sustentabilidade do assentamento Eldorado II no município de Sidrolândia, MS. 2012. 68 f. Dissertações de Mestrado em Meio Ambiente e Desenvolvimento Regional. Universidade Anhanguera – Uniderp.

PEREIRA, M. F.. Mensuramento da eficiência multidimensional utilizando analise de envelopamento de dados: revisão da teoria e aplicações. Dissertação (mestrado) - Universidade Federal de Santa Catarina, Centro Tecnológico. Disponível em https://repositorio.ufsc.br/xmlui/handle/123456789/76210. Acesso em 15/09/2015.

MDA. Territórios da Cidadania - Grande Dourados – MS. Disponível em http://www.territoriosdacidadania.gov.br/dotlrn/clubs/territriosrurais/grandedouradosms/one-community?page_num=0. Acesso em 12/11/2013.  

  ROLL, Y.; COOK, W.; GOLANY, B. Controlling Factor weights in DEA. II EE Transactions, Haifa, v. 23, p. 2-9, 1991.

MELLO, J. C. C. B. S.; GOMES, E. G.; MANGABEIRA, J. A. C. Análise de envoltória de dados para avaliação de eficiência e caracterização de tipologias em agricultura: um estudo de caso. RER, Rio de Janeiro, v. 43, n. 04, p. 607-631, 2005.

UFF – Universidade Federal de Fluminense. Software “Sistema Integrado de Apoio à Decisão – SIAD. Disponível em: http://www.uff.br/decisao. Acesso em: 20/05/2015. 

1. Professor do Mestrado em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp, Campo Grande, MS, (e-mail: csouza939@gmail.com).

2. Mestre em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp;

3. Mestre em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp;

4. Mestre em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp;

5. Professor do Mestrado em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp, Campo Grande, MS, (e-mail: jfreisneto@terra.com.br).

6. Professor do Mestrado em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp, Campo Grande, MS, (e-mail: danielfrainer@gmail.com).

7. Bolsista da Fundação Nacional de Desenvolvimento do Ensino Superior Particular (Funadesp) do Programa de Pós-Graduação em Meio Ambiente e Desenvolvimento Regional da Universidade Anhanguera Uniderp.