

Vol. 38 (Nº 14) Año 2017. Pág. 13
Jaime PADRON-CANO 1; Jairo R. CORONADO-HERNÁNDEZ 2; William CAICEDO-TORRES 3; Nohora MERCADO-CARUSO 4; Fairuz V. OSPINO-VADIRIS 5
Recibido: 26/09/16 • Aprobado: 27/10/2016
3. MRP basado en un algoritmo de nubes de partículas
RESUMEN: En este trabajo se aborda el problema de planificación de requerimiento de materiales (MRP) por medio de un algoritmo basado en enjambre de partículas. Se realizan diferentes experimentos por computadora con diferentes niveles de capacidad de producción donde el algoritmo mostró un buen desempeño. Se pueden observar que las soluciones de la adaptación del algoritmo de optimización por enjambre de partículas son mejor en un 6,31% a la presentada en la literatura estudiada. |
ABSTRACT: This work approaches the Material Requirements Planning (MRP) problem through a Particle Swarm Optimization (PSO) based algorithm. Results from various computer experiments are carried out considering different production capacity levels, where the algorithm shown good performance. It can be observed that the solutions found by the algorithm surpass by 6.31% the solution presented in the reviewed literature. |
La planificación de requerimientos de materiales (MRP) consiste en planear la fabricación o compra de componentes y de productos dando como resultado final la generación de órdenes de producción y compras considerando los tiempos, uso de recursos y operaciones asociadas. En un sistema MRP, la determinación de los tamaños de lote consiste en un conjunto de métodos o algoritmos para calcular en periodos discretos de tiempo las unidades a producir y en guardar para inventario de manera que se pueda satisfacer la demanda prevista (HERZER, MENEZES, POSSEBON, & NUNES, 2015; Orlicky, 1975). En (MOREIRA, PACAGNELLA, PACÍFICO, & SALGADO, 2014) se muestra que las empresas con métodos eficientes de planeación de la producción tienen ventajas competitivas frente a su competencia, dado que permite responder rápidamente a los requerimientos de los clientes. En esa dinámica, el concepto de tiempo, volumen y capacidad se vuelven variables cruciales de un sistema de fabricación, por lo que los clientes son sensibles a los plazos de entrega y la a calidad del servicio (SANA, ACEVEDO, & SALAS, 2014).
El sistema MRP fue propuesto por ORLICKY en 1975, basándose en un sistema de planeación multinivel con la finalidad de entregar el producto en el tiempo y cantidades requeridas donde el producto tiene una única lista de materiales. Con el tiempo este tipo de estructura de producto se llamó grafo Gozinto. En (BILLINGTON, MCMCLAIN, & THOMAS, 1983) se propone un modelo de optimización para resolver el problema MRP, equivalente a un modelo de planificación de materiales con restricciones de capacidad, conocido actualmente como MRP II. Todos los problemas postulados a partir de BILLINGTON, se basan en la misma lista de materiales tipo Gozinto. Este problema hace parte de una familia de problemas conocida como modelos CLSP (Capacitated Lot Sizing Problem) los cuales son de complejidad Np-Hard (FLORIAN, M.M LENSTRA, J. & RINOOY, 1980). A partir de ellos, diversos autores han planteado diversas heurísticas y meta heurísticas para abordar este problema. En (HAN, TANG, KAKU, & MU, 2009; WAJANAWICHAKON & PITAKASO, 2013) se presentan una implementación del algoritmo de enjambre de partículas para el problema de planificación de producción sin restricciones de capacidad en sistemas multinivel. En este trabajo se presenta una meta-heurística basada en el algoritmo de enjambre de partículas para resolver el problema de planificación de requerimiento de materiales (MRP) el cual es equivalente a un problema de planificación de la producción en sistemas multinivel con restricciones de capacidad.
Este artículo se estructura de la siguiente manera: en la primera sección se presenta la descripción matemática del problema. En la tercera sección se presenta el algoritmo propuesto. En la cuarta sección se presenta los resultados computacionales obtenidos a partir de la aplicación del algoritmo propuesto. Por último se presentan las conclusiones y referencias.
Para dar solución al problema del tamaño de lote multinivel capacitado aplicando optimización por enjambre de partículas se plantea una metodología que consiste en cuatro fases secuénciales: investigación, análisis, diseño y ejecución. Las fases que corresponden al esquema metodológico que se muestran en la Figura 1.
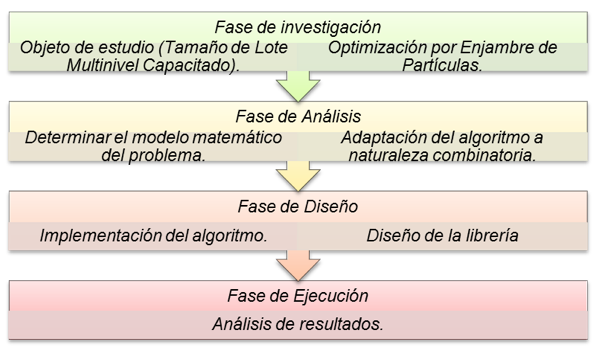
Figura 1 . Fases de la metodología de la investigación
Estas fueron las fases que orientaron el desarrollo de este trabajo. En la fase de investigación se revisó la bibliografía relacionada al problema del tamaño de lote multinivel capacitado con el fin de entender el contexto de este, sumado a la revisión del algoritmo de optimización por enjambre de partículas. En la fase de análisis se determinar el modelo matemático del problema con el fin formular la estructura del algoritmo, analizar las variables y parámetros del modelo, además determinar la relación entre estos. En la fase de diseño crea una arquitectura de software que será la base fundamental para la construcción de la herramienta computacional que permitirá la ejecución del algoritmo a partir de los requerimientos obtenidos en la fase de análisis. Por ultimo en la fase de ejecución, se realizar un análisis de los parámetros iniciales del algoritmo por medio de un caso de estudio.
El problema del tamaño de lote multinivel capacitado corresponde a una situación muy particular dentro de los sistemas de producción en empresas manufactureras, que juegan un papel importante debido a que puede convertirse en una oportunidad de mejora de procesos, esto con el fin de obtener una reducción de costos significativa para la empresa. El problema fue formulado matemáticamente en (Billington et al., 1983).
En el problema se busca la minimización de los costes asociados a manejo de inventario y al alistamiento del sistema de fabricación para la producción como se observa en la ecuación (1). Para ello hay una serie de limitaciones que restringen el espacio de soluciones. En la restricción (2) se presentan la continuidad del inventario, considerando la estructura del producto i representada por la matriz Gozinto aij y teniendo en cuenta para la producción de los componentes un tiempo de entrega LT(i). En la restricción (3) se presenta que hay una disponibilidad de tiempo para la producción y para la preparación de los equipos, la cual es limitada. Con la restricción (4) se asegura que si hay producción, entonces se realiza una preparación de los recursos productivos, los cuales consumen tiempo y un costo asociado. Por último se presentan las restricciones obvias en (5).

Una característica de los problemas de tamaño de lote multinivel es que poseen un amplio espacio de búsqueda es por ello que para encontrar una solución óptima el tiempo de solución aumenta exponencialmente, ya sea por el número de variables o por las restricciones, más aún, se hace mucho más complicado con la introducción de producción multinivel, debido a esto, éste problema es categorizado como NP-Hard, dado que la respuesta no se puede conocer de forma determinística y el cálculo para obtener la solución óptima se lleva a cabo en un tiempo polinomial.
Para determinar los niveles de tamaño de lote de cada componente en un sistema MRP se utilizará como método base la optimización por enjambre de partículas (Particle Swarm Optimization, por sus siglas en inglés). Este algoritmo fue propuesto por (Kennedy & Eberhart, 1995). Por medio este algoritmo, se determinará la matriz binaria de set up apropiada para cada solución. La fundamentación del algoritmo de optimización por enjambre de partículas implementado en este trabajo se basó en la propuesta por (Wajanawichakon & Pitakaso, 2013) agregando una matriz de velocidades para la adaptación a una naturaleza combinatoria. La estrategia utilizada se basa en una representación abstracta a través de la matriz binaria de los set ups que representa una partícula y se expresa como se muestra en (6).

La generación de la población inicial se realiza de forma aleatoria generando partículas binarias con una probabilidad uniforme de los valores de la matriz A de setups como se muestra en (9).
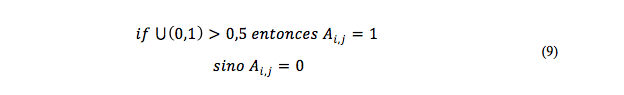
El valor de la velocidad de la partícula i en la dimensión d se establece como se muestra en (10).
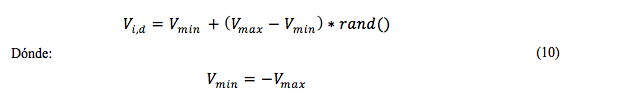
Para la generación de nuevas soluciones se utilizan dos funciones. En primera instancia, una función lineal a nivel de pieza para obligar a los valores de velocidad entre los valores permisibles máximos y mínimos, el intervalo [v_min,v_max ] se utiliza para controlar el valor a niveles mínimos y máximos como se muestra en la ecuación (11).
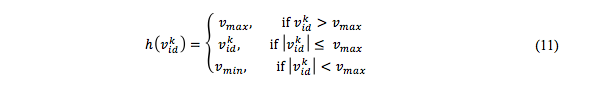
Una función sigmoide se utiliza para forzar los valores entre 0 o 1 después de la aplicación de la función lineal a nivel de pieza, la siguiente función sigmoidea se utiliza para escalar las velocidades entre 0 y 1, que luego se utiliza para convertir en valores binarios como se muestra en (12).

Nuevas partículas se encuentran mediante la actualización de la velocidad y la dimensión respectivamente. Calculamos la velocidad de actualización de vid^k con la siguiente ecuación (13). Luego se actualiza la velocidad vid mediante el uso de la función lineal h como se muestra en (14).

En la Figura 2 se observa el flujograma del algoritmo de nubes de particular que muestra todo el proceso explicado anteriormente para resolver el problema MRP considerando restricciones de capacidad. En misma figura, se observa una subrutina para la generación de partículas.
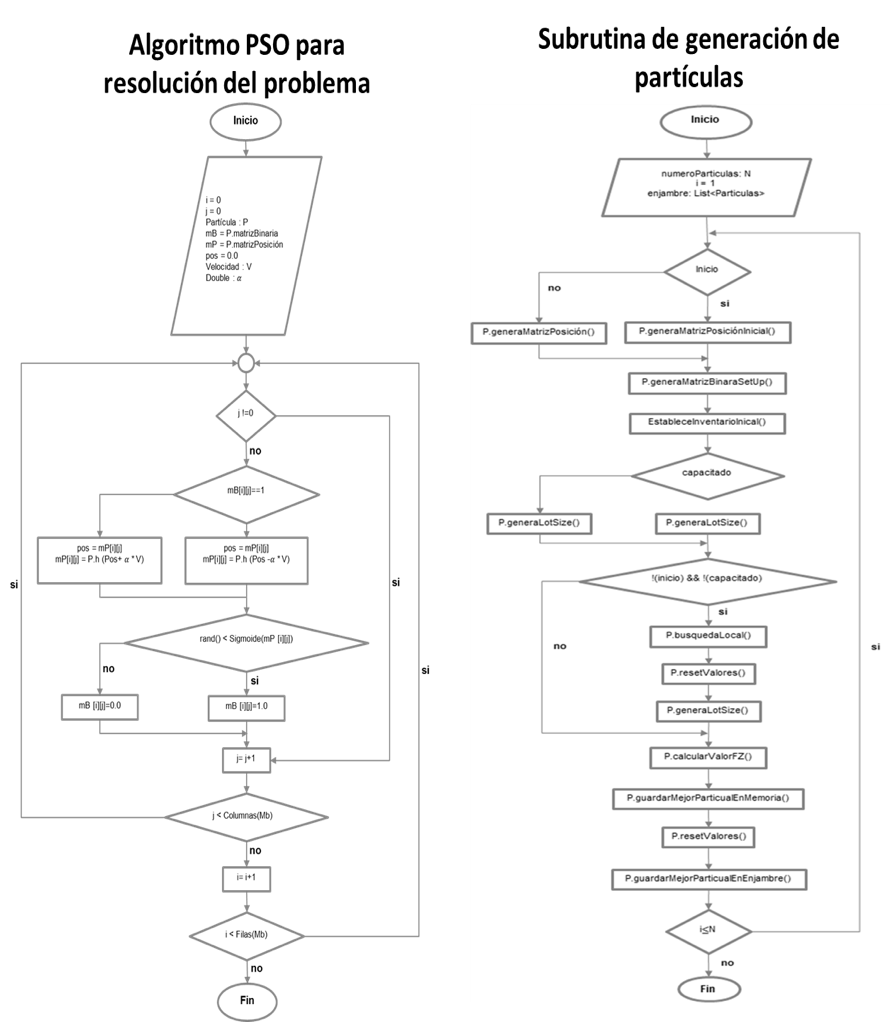
Figura 2. Flujograma de algoritmo PSO propuesto y subrutina de generación de partículas.
Luego, a cada partícula se le aplica un proceso de búsqueda local cuyo algoritmo se puede visualizar en la Figura 3 . Para ello se tienen en cuenta los parámetros del modelo tanto variables críticas como no críticas. En ese sentido, la heurística para resolver este problema se basa en que los tiempos de entregas son despreciables y cumple con la característica que la pendiente de la razón de los costos de almacenamiento y costos de set up es decreciente (Negativa); el propósito es realizar el set up de un producto (componente) de nivel inferior que salga más económico que mantener en inventario ese mismo producto, en consecuencia se puede afirmar que al momento de hacer un pedido de un producto se debe arrastrar la demanda de los componentes, es decir, presionar a los componentes a realizar un set up para tener inventario para satisfacer la demanda del producto de nivel superior.
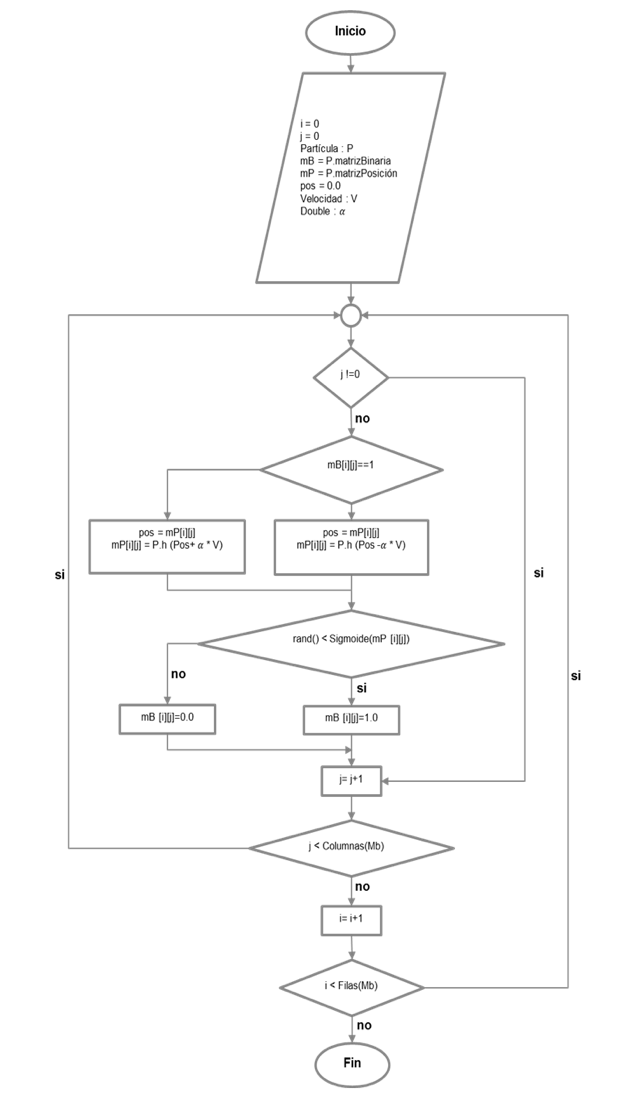
Figura 3. Algoritmo de búsqueda local para cálculo de stocks
Para el desarrollo del algoritmo se utilizó el lenguaje Java, por lo cual fue necesario definir una arquitectura en capas, por lo que se separa la capa de comunicación de los datos para el manejo de transacciones entre el modelo y la presentación. En la Figura 4 se muestra el diagrama de clases de la lógica del modelo, teniendo a la clase ModeloEnjambre y Partícula como la base principal del algoritmo PSO; la clase ModeloEnjambre está compuesta de muchas Partículas y un árbol de N-ario de la clase Producto, ésta y la clase Matriz están en el paquete utilidades que sirven para la representación del problema, cada partícula guarda en memoria múltiples referencias a la clase Matriz (Representación de una partícula).
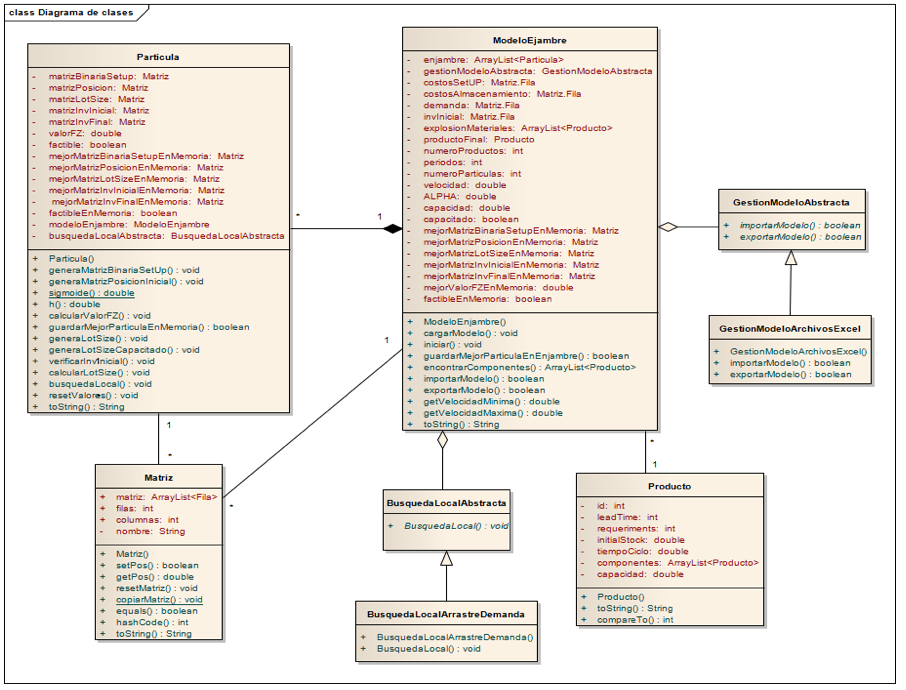
Figura 4 . Diagrama de clases de la lógica del algoritmo PSO propuesto
Existen dos representaciones abstractas para la gestión del modelo y la búsqueda local, diseñadas bajo el patrón de comportamiento “Estrategia”, este patrón de diseño permite mantener un conjunto de algoritmos de entre los cuales el objeto cliente puede elegir aquel que le conviene e intercambiarlo dinámicamente según sus necesidades, además le permite al software obtener la característica de extensible en diferentes contextos, éstas dos estrategias permiten importar y exportar el modelo a un archivo Excel (*.xls) y crear la búsqueda local conforme a la heurística propuesta para resolver el problema.
Para evaluar el desempeño del algoritmo presentado en este trabajo, se adaptaron los datos de (Han et al., 2009). La Tabla 1muestra la información del caso de estudio para probar el funcionamiento del algoritmo con una capacidad al 20%, 40% y 60% de la capacidad total del sistema. Los experimentos se realizaron en un computador con procesador AMD Phenom™ II N640 Dual-Core Processor 2.90 GHz, con 4,00 GB de memoria Ram, Sistema operativo Windows 7 Home Basic, modelo HP Pavilion dv5 Notebook. En la Tabla 1 se presentan los resultados obtenidos luego de haber ejecutado la aplicación 17 veces el algoritmo a partir de un muestreo estadístico con el propósito de realizar la selección de parámetros que mejore el desempeño del algoritmo.
Tabla 1 . Análisis de parámetros iniciales del algoritmo
Número de iteraciones |
||||||||||
100 |
300 |
500 |
||||||||
Velocidad |
Alfa |
20 |
40 |
60 |
20 |
40 |
60 |
20 |
40 |
60 |
4 |
0.2 |
2448,3 |
2303,6 |
2482,6 |
2399,3 |
2196,3 |
2746 |
2318,6 |
2195,6 |
2265,6 |
0.5 |
2249 |
2188 |
2325,3 |
2189,6 |
2386 |
2204,6 |
2368 |
2167,6 |
2202,6 |
|
0.9 |
2166 |
2163 |
1955,6 |
2144 |
2081,3 |
1978,3 |
2062,3 |
2043,3 |
1900,3 |
|
6 |
0.2 |
2218 |
2307,6 |
2193,3 |
2354,3 |
2198,3 |
2074,6 |
2488 |
2152,6 |
2124,6 |
0.5 |
2119 |
2089,3 |
2077,6 |
2182,3 |
1993 |
2016,3 |
2060,3 |
2028,6 |
2057,6 |
|
0.9 |
2257 |
2152,6 |
2123,6 |
2022 |
1974,3 |
2077 |
2038,3 |
2036,3 |
1950,3 |
|
10 |
0.2 |
2561,6 |
3033 |
2698,6 |
2404 |
2414,6 |
2614 |
2424,6 |
2432,3 |
2903,3 |
0.5 |
2186 |
2271 |
2194,6 |
2340 |
2051,3 |
2199,6 |
2277,6 |
2296,6 |
2066,6 |
|
0.9 |
2283,3 |
2201 |
2209,6 |
2410 |
2117,6 |
2232,3 |
2292,6 |
2339 |
2176,6 |
|
Cabe resaltar la importancia del factor alfa el cual no siempre ofrece buenas soluciones cuando se toma el valor de 0.2, además de mencionar que el peor promedio (2903,3) se dio cuando se evaluó el algoritmo con 500 iteraciones, 60 partículas, una velocidad de 10.0 y alfa de 0.2. El mejor promedio (1900,3) se dio cuando se evaluó el algoritmo con 500 iteraciones, 60 partículas, una velocidad de 4.0 y alfa de 0.9; a diferencia del peor caso, se intentó elevar la exploración con una velocidad más baja y explotar la búsqueda local con un alfa más alto.
Del análisis de estos parámetros se utilizó la combinación de 500 iteraciones, 60 partículas, una velocidad de 4,0 y un alfa de 0,9. Al ejecutar los experimentos utilizando los datos de (Han et al., 2009), se obtiene que el algoritmos PSO propuesto de buenos resultados frente al algoritmo PSO, un Algoritmo Genético propuesto y un algoritmo WW que se presentan en el trabajo de (Han et al., 2009), como se puede observar en la Tabla 2 .
Tabla 2 . Comparación de resultaos en modelo con (Han et al., 2009)
Algoritmo |
Mejor |
Peor |
Promedio |
Tiempo de ejecución |
PSO |
1895 |
2199 |
2008,4 |
7,3 |
PSO de (Han et al., 2009) |
1895 |
5565 |
2143, 9 |
5,3 |
AG |
1895 |
6446 |
2526,9 |
8 |
WW |
2123 |
2123 |
2123 |
<0,1 |
Se procede utilizar las misma instancia, pero adaptándola a un problema con capacidad limitada. Para ello, se plantea un recurso productivo que será utilizado para las operaciones de producción de componentes en todos los niveles. Con base a esto se propone analizar el desempeño para proveer soluciones factibles cuando el recurso no está al 100% correspondiente a la máxima ocupación del sistema según la demanda prevista. En la Tabla 3 se presentan los valores de la capacidad y los resultados obtenidos. El experimento se realizó mediante la evaluación del 20, 40 y 60% de la capacidad total del recurso para producir unidades del producto final en un período.
Tabla 3 . Resultados al agregar un recurso con capacidad limitada
|
Porcentaje de capacidad (%) |
||
Prueba |
20 |
40 |
60 |
Capacidad |
112 |
224 |
337 |
Fitness |
2775 |
2152 |
1939 |
Se observa que cuando entre menor sea la capacidad productiva, entonces se tiende a aumentar el coste total de producción. Esto se debe principalmente a que el sistema tiende a mantener más unidades en inventario para que en periodos donde hay picos de demanda, se pueda suplir esta por medio del inventario.
En este artículo, se presentó una meta heurística de enjambre de partículas para dar solución al problema de tamaño de lote multinivel capacitado el cual contempla una matriz de velocidades y un algoritmo de búsqueda local para mejorar el desempeño del algoritmo. Se logró reducir en un 6,31% los costes en un caso presentado en la literatura y disminuir la generación de malas soluciones. Ello llevo a la evaluación el mismo caso de estudio agregando la restricción en la fabricación del producto al 20%, 40 y 60%, en el que fue capaz de proveer soluciones factibles con un buen desempeño con base al modelo no capacitado.
Billington, P., McMclain, J., & Thomas, J. (1983). Mathematical programming approaches to capacity-constrained MRP systems: review, formulation and problem reduction. Management Science, 29(10), 1126 – 1141. Retrieved from http://pubsonline.informs.org/doi/abs/10.1287/mnsc.29.10.1126
Florian, M., Lenstra, J., & Rinooy, K. (1980). Deterministic production planning: algorithms and complexity. Management Science, 26, 669 – 679.
Han, Y., Tang, J., Kaku, I., & Mu, L. (2009). Solving uncapacitated multilevel lot-sizing problems using a particle swarm optimization with flexible inertial weight. Computers and Mathematics with Applications, 57(11-12), 1748–1755. doi:10.1016/j.camwa.2008.10.024
HERZER, M., MENEZES, F. M., POSSEBON, A. P., & NUNES, F. de L. (2015). Avaliação da utilização de metodologias ativas no ensino superior: estudo de caso na disciplina de gestão da produção aplicada. ESPACIOS, 37(2), E–3. Retrieved from http://www.revistaespacios.com/a16v37n02/163702e3.html
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Neural Networks, 1995. Proceedings., IEEE International Conference on, 4, 1942–1948 vol.4. doi:10.1109/ICNN.1995.488968
MOREIRA, E., PACAGNELLA, A. C., PACÍFICO, O., & SALGADO, A. P. (2014). Contribuições do planejamento e controle da produção para a competitividade empresarial: um estudo em uma empresa do setor moveleiro. Espacios, 35(9), 5. Retrieved from http://www.revistaespacios.com/a14v35n09/14350905.html
Orlicky, J. (1975). Material Requirements Planning. United States of America: McGraw –Hill.
Sana, S. S., Acevedo, J., & Salas, K. (2014). A three layer supply chain model with multiple suppliers, manufacturers and retailers for multiple items. Applied Mathematics and Computation, 229, 139–150. doi:10.1016/j.amc.2013.12.006
Wajanawichakon, K., & Pitakaso, R. (2013). Solving large unconstrainted multi level lot-sizing problem by a binary particle swarm optimization. International Journal of Management Science and Engineering Management.
1. Ingeniero Industrial y de Sistemas. Especialista en Ingeniería de Software. Desarrollador de Bases de Datos en ProutLoud Media Networks. Medellín, Colombia. jaimepc199@gmail.com
2. Doctor Ingeniero Industrial. Profesor Titular del Departamento de Ingeniería Industrial. Líder grupo de investigación PRODUCOM. Universidad de la Costa. Barranquilla, Colombia. jcoronad18@cuc.edu.co
3. Máster en Ingeniería de Sistemas. Profesor Asistente. Universidad Tecnológica de Bolívar. Cartagena de Indias, Colombia. wcaicedo@unitecnologica.edu.co
4. Máster en Ingeniería de Sistemas. Profesor Adjunto. Universidad de la Costa. Barranquilla, Colombia. nmercado1@cuc.edu.co
5. Ingeniera Industrial. Decano Facultad de Ingeniería. Universidad de la Costa. Barranquilla, Colombia. fospino@cuc.edu.co