 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 17) Año 2016. Pág. 16
Vinícius Rafael BIANCHI 1; Sandra Cristina de OLIVEIRA 2; Leonardo de Barros PINTO 3; Ana Cláudia ANDREOLI 4; Guilherme Besse GARNICA 5
Recibido: 25/02/16 • Aprobado: 03/04/2016
RESUMO: O agronegócio é uma das atividades mais importantes da economia brasileira e do estado de São Paulo, apresentando diversidades de produção, formas de produção, organização e formação social. O objetivo deste trabalho foi identificar clusters ou agrupamentos de municípios da região do Médio Paranapanema, no estado de São Paulo, Brasil, de acordo com sua produção agropecuária e área plantada registradas pelo Instituto de Economia Agrícola no ano de 2013, buscando avaliar quais produtos, dentre os que mais se destacaram em 2013 na referida região (cana de açúcar, mandioca, milho e soja), têm contribuído para o desenvolvimento socioeconômico de cada cluster formado na região. |
ABSTRACT: Agribusiness is one of the most important activities of the national economy and the state of São Paulo, with production diversity, forms of production and social formation. The objective of this study was to identify clusters or groupings of municipalities in the Middle Paranapanema, in the state of Sao Paulo, Brazil, according to their agricultural production and acreage registered by the Institute of Agricultural Economics in 2013, seeking to evaluate which products, among those who stood out in 2013 in that region (sugar cane, cassava, corn and soybeans), have contributed to the socioeconomic development of each cluster formed in the region. |
O agronegócio é uma das atividades mais importantes da economia brasileira. De acordo com o MAPA (2010), 26,5% do Produto Interno Bruto (PIB) do Brasil é composto pelo setor agrícola, que apresenta diversidade em vários aspectos, nas mais diversas regiões brasileiras. Além disso, o agronegócio tem sido responsável por quase 40% do emprego formal e 36% das exportações brasileiras, sendo o setor que mais tem contribuído para o equilíbrio das contas externas (MENDES; PADILHA JR., 2007).
Pelo relevante papel que desempenham no suprimento de alimentos e na geração de emprego e renda para a população brasileira, especificamente para o estado de São Paulo, quatro das principais culturas que se destacam no agronegócio são: cana de açúcar, mandioca, milho e soja, as quais serão elementos deste estudo.
O Estado de São Paulo é destaque nacional no setor agrícola, com várias culturas e regiões relevantes ao agronegócio, sendo responsável por um terço do PIB agroindustrial do Brasil. Historiadores relatam que o estado nasceu a partir da agricultura; Da incipiente pecuária extensiva, as fazendas foram nascendo e, do café cultivado, as cidades foram se formando (SAMPAIO 2009).
Ainda segundo SAMPAIO (2009):
O estado de São Paulo, visto como a unidade mais industrializada da nação, é também a sua maior plataforma agrícola, respondendo por quase 20% do valor bruto da produção agropecuária brasileira. Em 2008, nas propriedades paulistas foram gerados quase R$ 38 bilhões em valor da produção. Se contar a cadeia do agronegócio, pode-se multiplicar esse montante por dez – o chamado depois da porteira.
Dentre as regiões paulistas com economia baseada no agronegócio encontra-se a região do Médio Paranapanema, a qual tem significativa importância econômica para o estado, principalmente devido à cultura da cana de açúcar (UDAETA, 2004).
A região do Médio Paranapanema possui extensão de 6.237 km2 e está situada entre as bacias dos rios Paranapanema e do Peixe (UDAETA, 2004). É formada pela comarca de Governo de Assis mais alguns municípios associados ao Consórcio Intermunicipal do Vale do Paranapanema. Assim, é composta por 18 municípios, sendo estes: Assis, Campos Novos Paulista, Cândido Mota, Cruzália, Echaporã, Florínia, Ibirarema, Iepê, Lutécia, Maracaí, Nantes, Oscar Bressane, Palmital, Paraguaçu Paulista, Pedrinhas Paulista, Platina, Quatá e Tarumã.
Dada a amplitude e a diversidade agrícola desta região, a identificação de clusters ou grupos de municípios, de acordo com suas respectivas produções agropecuárias, é relevante para promover análises socioeconômicas e ambientais, dentre outras, que possam contribuir para o seu desenvolvimento.
O objetivo principal deste trabalho foi identificar clusters ou agrupamentos de municípios da região do Médio Paranapanema, de acordo com a produção agropecuária e a área plantada registradas pelo Instituto de Economia Agrícola (IEA) no ano de 2013, buscando avaliar quais produtos, dentre os que mais se destacaram em 2013 na referida região (cana de açúcar, mandioca, milho e soja), têm contribuído para o desenvolvimento socioeconômico de cada cluster formado na região. Para tanto, o presente estudo foi desenvolvido em quatro etapas. Na primeira foram buscados na literatura importantes trabalhos ligados ao tema; na segunda etapa foram apresentados os procedimentos de coleta de dados e de análise multivariada (fatorial e de clusters), na terceira foram feitas análise e discussão dos resultados obtidos; e, na última etapa foram apresentadas algumas conclusões pautadas nos referidos resultados.
As técnicas estatísticas de análise fatorial e de análise de clusters ou de agrupamentos têm sido amplamente utilizadas em pesquisas sobre o agronegócio. São técnicas que auxiliam na resolução de problemas a partir de um grande número de variáveis a serem analisadas.
A análise fatorial é uma técnica que busca, por meio da avaliação de um conjunto de variáveis, a identificação de dimensões de variabilidade comuns existentes em um conjunto de fenômenos; o intuito é desvendar estruturas existentes, mas não observáveis diretamente. Cada uma dessas dimensões de variabilidade comum recebe o nome de fator. Resumidamente, a Análise Fatorial tem como um de seus principais objetivos descrever um conjunto de variáveis originais por meio da criação de um número menor de dimensões ou fatores. (Corrar et al., 2009).
A análise de clusters ou de agrupamentos consiste em uma técnica multivariada com o intuito de classificar objetos, de modo que cada objeto seja muito semelhante aos outros no agrupamento, em relação a algum critério de seleção pré-determinado. Os agrupamentos resultantes de objetos devem possuir elevada homogeneidade interna (dentro dos agrupamentos) e elevada heterogeneidade externa (entre agrupamentos) (Hairet al., 2005).
Encontram-se na literatura diversas pesquisas nacionais e internacionais ligadas ao termo agronegócio que utilizaram técnicas estatísticas de análise fatorial e de análise de clusters na resolução de problemas.
Em um estudo utilizando análise fatorial e análise de clusters, Inderhess e Theuvsen (2009) lidaram com a tomada de decisão estratégica por parte dos agricultores alemães, que eram confrontados com novas ameaças e oportunidades. Os resultados empíricos mostraram que os agricultores empregavam uma ampla gama de estratégias corporativas, competitivas, funcionais e cooperativas para reposicionar suas fazendas, em face de mudança de ambientes econômicos e políticos. Esse estudo permitiu aos agricultores identificarem as lacunas estratégicas frente à mercados globalizados.
Popovic et al. (2011) utilizaram análise de clusters para determinar como os municípios da República da Sérvia eram agrupados de acordo com o nível de desenvolvimento das pequenas e médias empresas do agronegócio. Com isso, obtiveram percepções sobre a condição atual do desenvolvimento regional desse setor, bem como a possibilidade de desenvolvimento dos municípios menos desenvolvidos na Sérvia. Sua análise permitiu formar nove grupos homogêneos de municípios, cada grupo com suas próprias características especiais em termos da intensidade de alguns dos indicadores observados.
Mais recentemente, Adhikari et al. (2012) retrataram projetos agrícolas desenvolvidos pelo governo do Nepal, os quais não adotavam uma perspectiva por parte do consumidor. Abordaram essa lacuna por meio do levantamento de consumidores de tomates no Nepal, segmentando-os por meio de análise de clusters e monstrando como a segmentação de consumidores poderia fornecer orientação estratégica para o desenvolvimento da cadeia de valor. A pesquisa identificou quatro segmentos distintos de consumidores de tomate em Kathmandu. Uma análise das cadeias de abastecimento existentes mostrou discrepâncias entre as expectativas do consumidor e a entrega de valor, sugerindo oportunidades de melhoria ao desenvolvimento dessas cadeias.
Peres Jr. et al. (2013) buscaram identificar padrões que caracterizavam a agricultura familiar em sua assimetria e elementos distintivos utilizando os dados do Censo da Agricultura 2006, para avaliar a sua composição e distribuição entre os municípios de Minas Gerais. Objetivaram identificar o seu perfil e sua contribuição para o desenvolvimento econômico e social do referido estado, utilizando as técnicas de análise fatorial e de análise de clusters. Os resultados mostraram que características distintas marcavam a agricultura familiar nas cidades relacionadas do estado de Minas Gerais, principalmente com condições socioeconômicas, o que implicava, portanto, realidades alternativas nos municípios.
Para Callado e Soares (2014), a análise de clusters teve como objetivo identificar a estrutura e padrões de relações entre os indicadores de desempenho utilizados dentro de organizações paraibanas ligadas ao agronegócio. Em sua pesquisa, investigaram 32 indústrias e analisaram dez indicadores de desempenho. Os resultados mostraram evidência empírica da existência de relações entre vários indicadores de desempenho a partir da identificação de dois grupos distintos. O primeiro grupo era composto dos indicadores identificados de rentabilidade, serviço e satisfação dos funcionários pós-venda. O segundo grupo foi composto por indicadores de rentabilidade e satisfação do cliente.
Portanto, pela sua relevante aplicabilidade, as técnicas estatísticas multivariadas, análise fatorial e análise de clusters, mostram-se como ferramentas importantes para a resolução de problemas relacionados ao agronegócio, contribuindo nas tomadas de decisões desse segmento.
Tratou-se de uma pesquisa exploratória com abordagem quantitativa. Assim, foram coletados dados secundários do Instituto de Economia Agrícola (IEA), especificamente, dados de produção agropecuária e de área produzida na safra do ano de 2013 nos 18 municípios que compõem a região do Médio Paranapanema, já citados anteriormente.
Para tanto, foram identificados os produtos agropecuários que mais se destacaram nesta região na referida safra, ou seja, aqueles que se destacaram tanto em área produtiva (em hectares) quanto em quantidade de produção (em toneladas). Assim, de acordo com os dados, os quatro produtos resultantes dessa filtragem foram: a cana de açúcar, a mandioca, o milho e a soja, respectivamente.
A análise dos dados coletados foi feita por meio de uma abordagem estatística multivariada, utilizando análise fatorial e análise de clusters. Devido ao grande número de variáveis em estudo, a análise fatorial e a análise de clusters são ferramentas úteis para o alcance dos objetivos, uma vez que podem ser empregadas quando se deseja reduzir o número de objetos (isto é, o número de linhas numa matriz de observações por variáveis), agrupando-os em clusters (Corrar et al., 2009).
Para a análise foram utilizadas quatorze variáveis relacionadas aos produtos cana-de-açúcar para a indústria (CANA.I.A e CANA.I.P) e cana-de-açúcar para forragem (CANA.F.A e CANA.F.P), mandioca para indústria (MAND.I.A e MAND.I.P) e mandioca para a mesa (MAND.M.A e MAND.M.P), milho (MILHO.A e MILHO.P) e milho safrinha (MILHO.S.A e MILHO.S.P) e soja (SOJA.A e SOJA.P), estando especificado para cada produto a área utilizada para a cultura do mesmo (.A) e a quantidade de produto produzida (.P).
A partir dos dados coletados estimou-se a matriz de correlação amostral R14x14, com a qual se comprovou a aplicabilidade do modelo fatorial, uma vez que as variáveis mostraram-se correlacionadas.

Formando a notação matricial, tem-s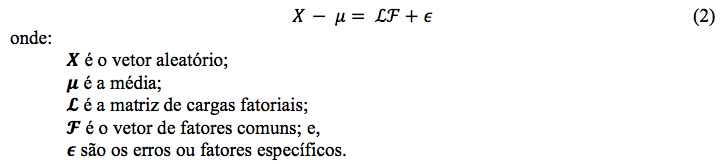
Com tantas quantidades não observáveis, uma verificação direta do modelo fatorial a partir de observações é impraticável. Porém, algumas suposições adicionais sobre os vetores ![]() e ϵ implicam em certas relações de covariância que podem ser verificadas (MINGOTI, 2005).
e ϵ implicam em certas relações de covariância que podem ser verificadas (MINGOTI, 2005).
De acordo com Mingoti (2005), tem-se:
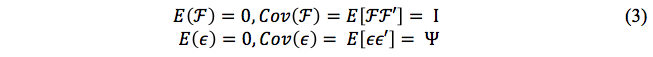
Sabendo que ![]() e ϵ são independentes, tem-se:
e ϵ são independentes, tem-se:
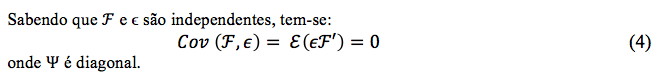
Com as suposições levantadas sobre a matriz de covariância Ʃ e o vetor aleatório X tem-se:
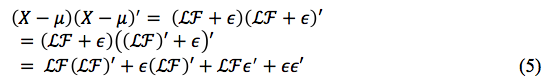
Então:
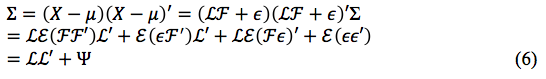
Após a análise de tais suposições, analisou-se a comunalidade, ou seja, a porção da variância da i-ésima variável explicada por n fatores comuns, por meio da seguinte função:

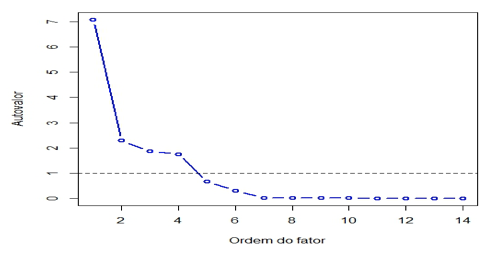
Neste trabalho, para a definição do total de fatores a serem utilizados, estimou-se também os autovalores da matriz de correlação, tendo sido utilizado como critério o menor número de fatores possíveis, objetivando a simplificação da análise. A Figura 1 mostra os resultados do cálculo dos autovalores.
Figura 1- Gráfico Scree-plot com p=14.
Fonte: Elaborada pelos autores a partir dos dados do IEA (2014).
Figura 2- Escores do CP1 e CP2.
Fonte: Elaborada pelos autores a partir dos dados do IEA (2014).
Por meio dos autovalores observados na Figura 1, pode-se definir de dois a quatro o números de fatores necessários para a análise dos dados. Como o objetivo é uma análise mais simplificada, foram utilizados dois fatores, sem nenhum prejuízo para as análises feitas, pois estes fatores representavam 67% da variância total.
Para cada município foi calculado o coeficiente relacionado com cada um dos fatores (F1 e F2) por meio do método dos componentes principais, sendo realizada a decomposição espectral da matriz R14x14 para obtenção da matriz L, que contêm os fatores desejados e a matriz de variabilidade Ψ (MINGOTI, 2005).
Para a confirmação dos resultados obtidos com a análise fatorial e uma melhor visualização das similaridades entre os municípios, foi realizada a análise de clusters aos dados, com a aplicação das distâncias médias, onde o menor valor da distância representa maior similaridade dos municípios.
O método das distâncias médias se resume a cinco passos, sendo eles (BUSSAB, 1990):
1 – Determina-se a matriz de distâncias inicial; 2 – Localizam-se os dois elementos que apresentam a menor distância, reunindo em um único grupo; 3 – Calcula-se a distância entre os diversos pares de grupos como sendo a média das distâncias entre os pares de seus elementos, sendo um elemento de cada um dos grupos. 4 – Reúnem-se os dois grupos que apresentarem menor distância em um único grupo; e 5 – Termina-se o processo se o número de grupos obtidos for igual a um número q ≤ n, caso contrário, retorna-se ao passo 3.
Este método consiste em considerar que a distância entre dois grupos é a média de todas as distâncias entre pares de elementos (um em cada grupo) (JOHNSON; WICHERN, 1998). As distâncias médias são dadas por:

Com o uso da metodologia da análise fatorial foram definidos dois componentes principais (CP1 e CP2), que representam 67% da variância total dos dados, relacionados na Tabela 1 com as 14 variáveis iniciais.
Tabela 1- Cargas Fatoriais.
Variáveis |
CP1 |
CP2 |
CANA.I.A |
0,277 |
0,629 |
CANA.I.P |
0,284 |
0,681 |
CANA.F.A |
-0,466 |
-0,033 |
CANA.F.P |
-0,438 |
-0,018 |
MAND.I.A |
0,387 |
-0,709 |
MAND.I.P |
0,445 |
-0,695 |
MAND.M.A |
0,722 |
0,433 |
MAND.M.P |
0,731 |
0,422 |
MILHO.A |
0,880 |
-0,207 |
MILHO.P |
0,921 |
-0,140 |
MILHO.S.A |
0,921 |
-0,033 |
MILHO.S.P |
0,921 |
0,050 |
SOJA.A |
0,944 |
-0,085 |
SOJA.P |
0,952 |
-0,054 |
Fonte: Elaborada pelos autores a partir dos dados do IEA (2014).
Na Tabela 1 estão destacadas ainda as maiores cargas fatoriais para cada variável. A análise destas cargas fatoriais permite concluir que o fator CP1 está diretamente relacionado à produção de mandioca para mesa, milho e soja e o fator CP2 está diretamente relacionado à produção de cana para indústria e inversamente relacionada à produção de mandioca para a indústria. As variáveis relacionadas à produção de cana para forragem estão pouco representadas por estes fatores, pois esta cultura é menos representativa quando comparadas com as culturas de cana para indústria. No entanto, esta menor representação não dificulta a análise dos dados.
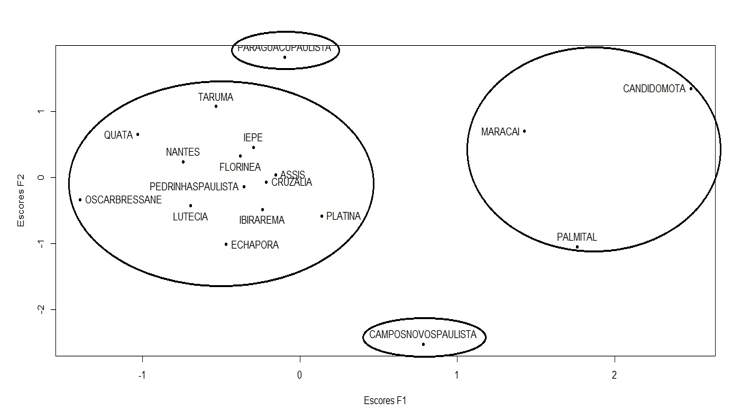
Os municípios analisados foram divididos em quatro grupos por meio da análise fatorial do gráfico da pontuação (escores), para cada componente principal definido, conforme a Figura 2.
Figura 2- Escores do CP1 e CP2.

Fonte: Elaborada pelos autores a partir dos dados do IEA (2014).
O primeiro grupo identificado é formado pelos municípios Candidomota, Maracaí e Palmital, que apresentaram valores altos para os fatores CP1 e CP2. Estes municípios são grandes produtores de milho, soja e cana para indústria.
O segundo grupo identificado é formado pelo município de Campos Novos Paulista, que apresenta um valor alto para o fator CP1 e um valor baixo para o fator CP2. Este município é um grande produtor de mandioca, soja e milho, porém produz pouca cana quando comparado com os demais municípios da região.
O terceiro grupo identificado é formado pelo município Paraguaçu Paulista, que apresenta um valor alto para o fator CP2 e um valor baixo para o fator CP1. Este município é grande produtor de cana para indústria, porém produz pouca mandioca, milho e soja.
O quarto grupo é formado pelos demais municípios, que apresentam baixos valores para os fatores CP1 e CP2 e, portanto, possuem uma produção intermediária para todas as culturas, não sendo destaque em nenhuma delas.
Para a confirmação da existência e uma análise mais detalhada destes grupos foi realizada a análise de clusters, por meio da metodologia das distâncias médias, conforme o dendrogama da Figura 3.
Figura 3- Dendrogama por distância média.
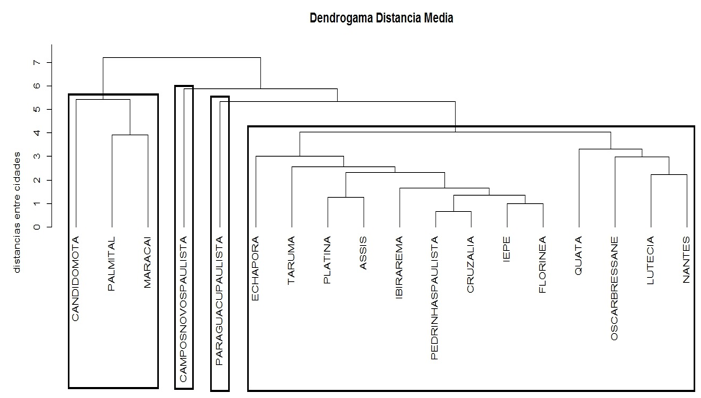
Fonte: Elaborada pelos autores a partir dos dados do IEA (2014).
A análise de clusters ou agrupamentos confirmou a existência dos grupos homogêneos encontrados na análise fatorial.
Quanto às variáveis relacionadas à cultura da mandioca, têm-se os municípios com maior produção espalhados nos quatro grupos formados. Como exemplo, tem-se: o maior produtor é o município de Campos Novos Paulista, classificado no grupo dois, o segundo produtor é o município de Palmital, classificado no grupo um, o terceiro produtor é Echaporã, classificado no grupo quatro e o quarto produtor é Candidomota, classificado no grupo um.
As análises apresentadas permitiram identificar grupos de municípios dentro da região do Médio Paranapanema, de acordo com sua produção agropecuária e área plantada, que mais se destacaram na safra do ano de 2013.
Assim, foram identificados quatro grupos: o primeiro composto por três cidades, Candidomota, Maracaí e Palmital, cujas produções em destaque foram de Milho, Soja e Cana de Açúcar; o segundo grupo formado pelo município de Campos Novos Paulista, com destaque para as produções de soja e milho; o terceiro grupo formado pelos municípios de Quatá e Paraguaçu Paulista, onde o destaque é para a produção de cana de açúcar; e, o quarto e último grupo composto pelos 12 municípios restantes da região e que possui grande diversidade em suas produções com a produção de cana de açúcar, mandioca, milho e soja, não tendo grande destaque em nenhuma das produções.
Cabe destacar neste estudo as variáveis relacionadas à cultura da mandioca, a qual possui relevância em municípios que estão espalhados em três grupos entre os quatro formados. O maior produtor, município de Campos Novos Paulista, encontra-se no grupo dois, Palmital e Candido Mota, segundo e quarto maiores produtores, respectivamente, estão no grupo um e Echaporã, terceiro colocado na produção, está no grupo quatro. O que aponta um produto com destaque em 75% dos clusters formados na região.
Sabe-se que a diversificação da produção agropecuária em determinadas regiões é condicionada por fatores socioeconômicos, ambientais e tecnológicos, dentre outros. E que estes ao longo do tempo, de acordo com a maior influência de um ou de outro, interferem sobremaneira na configuração da exploração dos sistemas agrários ou agro ecossistemas existentes.
Tanto na esfera pública, quanto privada, a identificação de clusters ou grupos de municípios em uma determinada região pode permitir a criação de propostas de desenvolvimento local e, ou regional, adaptadas às necessidades específicas de cada produção em determinado período ou ciclo da história, ou até mesmo a alternativas produtivas que levem à exploração de áreas com novos produtos.
Ainda que não se deva atribuir mudanças a um único fator, propostas como incentivo à implantação de indústrias processadoras, melhorias nos sistemas de logísticas de compras de insumos e de escoamento da produção, bem como de aumento da comercialização dessas produções, poderão favorecer o produtor rural e a geração de empregos na região.
A região do Médio Paranapanema apresentou quatro grupos com diferentes destaques de produção, de acordo com os quatro produtos selecionados. E, um produto, no caso a mandioca, se sobressaiu nos grupos encontrados, com municípios ocupando as primeiras colocações em nível de produção. Portanto, tais resultados dão indícios de que as quatro regiões dentro do Médio Paranapanema possuem potencial para o desenvolvimento local a partir da cultura da mandioca, mas sinalizam prováveis mudanças, cumprindo as possíveis alterações cíclicas, que passem a contemplar culturas como milho, soja e cana de açúcar. O que levaria, obrigatoriamente, a revisões de planos e estratégias que assegurem o desenvolvimento da região como um todo, bem como os custos sociais envolvidos, a saber: recolocação profissional das pessoas, combate ao desemprego nos períodos de ajuste, etc.
ADHIKARI, R.P.;COLLINS, R.; SUN, X. Segmenting Consumers to Inform Agrifood Value Chain Development in Nepal. International Food and Agribusiness Management Review. 15 (4), pp. 93-114, 2012.
BUSSAB,W.O.; MIAZAKI, E.S; ANDRADE, D.F. (1990). Introdução à Análise de Agrupamentos. 9o. SINAPE – Simpósio Nacional de Probabilidade e Estatística. IME – USP. São Paulo: Associação Brasileira de Estatística.
CALLADO, A.L.C.; SOARES, K.R. Analysis of the use of performance indicators in the contexto of agribusiness.Custos e Agronegócio. 10 (2), pp. 272-284, 2014.
CORRAR, L. J.; PAULO, E.; FILHO, J. M. D. Análise Multivariada para cursos de Administração, Ciências Contábeis e Economia. 1a Ed. São Paulo: Ed. Atlas, 2009.
HAIR JR., J. F.; ANDERSON, R. E.; TATHAM, R. L.; BLACK, W. C. Análise Multivariada de Dados. 5a Ed. Porto Alegre: Ed. Bookman, 2005.
IEA. Instituto de Economia Agrícola. Disponível em:< http://ciagri.iea.sp.gov.br/nia1/subjetiva.aspx?cod_sis=1&idioma=1 >. Acesso em: 03 nov.2014
INDERHEES, P.G.;THEUVSEN, L. Farmers' strategies in globalizing markets: Empirical results from Germany. Journal of International Food and Agribusiness Marketing. 21 (4), pp. 253-268, 2009.
JOHNSON, R. A.; WICHERN, D.W. Applied Multivariate Statitical Analysis, 4th ede., New Jersey: Prentice-Hall, 1998.
MAPA. A Força da Agricultura 1860 a 2010. Disponível em: < http://www.agricultura.gov.br/home/a_forca_da_agricultura2010.pdf >. Acesso em: 03 nov.2014.
MENDES, J. T. G.; PADILHA JR., J. B. Agronegócio: uma abordagem econômica. São Paulo: Pearson Education do Brasil, 2007.
MINGOTI, S.A. Análise de Dados Através de Métodos de Estatística Multivariada: Uma Abordagem Aplicada. Belo Horizonte: Editora UFMG, 2005
PERES JR., M.R.; PEREIRA,V.G.; DE LIMA SIQUEIRA, P.H.; ANTONIALLI, L.M. Caracterização e agrupamento de municípios de minas gerais em relação à agricultura familiar.Revista Brasileira de Gestao e Desenvolvimento Regional. 9 (3), pp. 75-99, 2013.
POOLE, N.D.Production and marketing strategies of Spanish citrus farmers. Journal of Agricultural Economics. 51 (2), pp. 210-223, 2000.
POPOVIC, B.; MALETIC, R., CERANIC, S., PAUNOVIC, T., SOJA, S.J. Defining homogenous areas of Serbia based on development of SME in agribusiness using the cluster analysis. Technics Technologies Education Management . 6 (3), pp. 811-818, 2011.
SAMPAIO, J. A Agricultura paulista de ontem, hoje e amanhã. Revista Agroanalysis Especial Agricultura de São Paulo Edição Março de 2009. Disponível em: < http://www.agroanalysis.com.br/especiais_detalhe.php?idEspecial=40 >. Acesso em: 05 set. 2014.
UDAETA, M. E. M.; INO, W. T.; GRIMONI, J. A. B.; GALVÃO, L. C. R., "Proposição para o Interior Paulista do Planejamento Integrado de Recursos". GEPEA-USP1. Mestre em Agronegócio e Desenvolvimento pela Universidade Estadual Paulista – UNESP, Docente da Faculdade Anhanguera, Bauru/SP, Brasil. e-mail: vini_bianchi@hotmil.com
2. Doutora em Ciências de Computação e Matemática Computacional pela Universidade de São Paulo – USP, Docente da Faculdade de Ciências e Engenharia da Universidade Estadual Paulista – UNESP, Campus de Tupã/SP, Brasil. E-mail: sandra@tupa.unesp.br
3. Doutor em Engenharia Agrícola pela Universidade de Campinas – UNICAMP, Docente da Faculdade de Ciências Agronômicas da Universidade Estadual Paulista – UNESP, Campus de Botucatu/SP, Brasil. E-mail: leo@fca.unesp.br
4. Mestranda do Programa de Pós Graduação em Engenharia de Produção da Universidade Estadual Paulista – UNESP, Funcionária Pública, Bancária no Banco Caixa Econômica Federal em Bauru/SP, Brasil. E-mail: ac.andreoli13@gmail.com
5. Mestrando do Programa de Pós-graduação em Engenharia de Produção da Universidade Estadual Paulista – UNESP, Funcionário Público, Auditor Fiscal do Trabalho do Ministério do Trabalho e Emprego em Bauru/SP, Brasil. E-mail: guilhermebesse@gmail.com