HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 03) Año 2016. Pág. 15

Modelos univariados e multivariados aplicados à previsão de valores de exportação: uma análise comparativa para o complexo soja

Univariate and multivariate models applied to the forecast of the monthly values of Brazil's soy complex export

Nicole Rennó CASTRO 1; Leandro GILIO 2; Adriana Ferreira SILVA 3; Vitor Augusto OZAKI 4

Recibido: 16/09/15 • Aprobado: 23/10/2015

Contenido

1. Introdução

2. Metodologia

3. Descrição dos dados

4. Resultados e Discussão

5. Conclusões

6. Referências

1. Introdução

A pauta de exportações brasileiras é historicamente caracterizada pela liderança de produtos de base primária na sua composição de receitas. Nas últimas décadas, as exportações brasileiras de commodities, graças à eficiência do setor, viabilizaram avanços no mercado externo, sendo determinante para tornar o Brasil – um secular devedor externo – em credor internacional. Tudo isso num contexto em que a formação de preços se dá essencialmente no exterior, ficando o país como um tomador de preços. Segundo estimativas do Cepea (2015), com dados do MDIC, a receita gerada com exportações de produtos do agronegócio alcançaram US$ 98 bilhões em 2014, alta de 367% frente à média registrada em 2000.  Deste total, o complexo da soja (farelo, óleo e grão) se destaca, sendo responsável por US$ 31,4 bilhões em 2014, ou 32% das exportações de produtos do agronegócio.

Em 2014, o país foi responsável por 29,6% da safra mundial do grão, avaliada em 319,4 milhões de toneladas (Figura a). Os Estados Unidos despontam como o principal produtor com 33,8% da produção mundial em 2014.

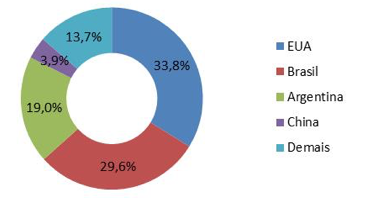
Figura a – Composição da produção mundial de soja (milhões de toneladas) - 2014
Fonte: Elaboração própria a partir de dados do USDA (2015)

Este elevado grau dependência do complexo soja na pauta exportadora do agronegócio e por fim, na economia brasileira, expõe o país a volatilidade de preços, afetando as receitas cambiais e fiscais, e, no longo prazo, as decisões de investimentos. Diante desta perspectiva, torna-se cada vez mais importante que as organizações públicas e privadas realizem estudos que compreendam a previsibilidade de indicadores relacionados ao setor agroexportador do complexo soja, em suas diversas dimensões e inter-relações, de modo a fornecer subsídios a um direcionamento mais eficiente de esforços e recursos, no curto e longo prazos.

Periodicamente, o Ministério da Agricultura, Pecuária e Abastecimento (MAPA) realiza o relatório "Brasil Projeções do Agronegócio", onde são apresentadas projeções para diversos produtos do agronegócio brasileiro (Brasil, 2012). No caso do complexo soja, o estudo baseia-se em modelos autorregressivos integrados de médias móveis (ARIMA), que apresentaram o melhor ajuste a série de dados, conforme os critérios de informação de Akaike Information Criterion (AIC) e de Schwartz Bayesian Criterion (SBC). Mas o uso de modelos univariados não permite agregar à análise a inter-relação entre variáveis que podem exercer grande influência nos dados de exportação do setor.

Paralelamente, Coronel et al. (2008) destaca duas importantes mudanças institucionais que exerceram influência sobre o valor exportado do complexo soja: a Lei Kandir (Lei Complementar n. 87, de 13 setembro de 1996) e a desvalorização cambial ocorrida a partir de 1999. Outro componente de influência direta sobre as séries de valor exportado é a dinâmica do preço internacional, que para o caso dos produtos agrícolas vem demandando especial atenção em estudos recentes, tendo em vista as fortes oscilações de preços acima comentadas (Black, 2013; Veríssimo; Xavier; Vieira, 2012; Banco Mundial, 2010).

Entre os modelos de séries temporais, uma maneira de captar o efeito dessas mudanças institucionais sobre as séries de tempo é por meio de modelos de intervenção, extensão dos modelos ARIMA, incorporando efeitos de choques exógenos sobre a variável de interesse. Essa metodologia pode possibilitar um melhor ajuste da estimação à série de dados e vem sendo utilizada na análise de séries de exportação para quantificar e avaliar o efeito de políticas ou mudanças institucionais que alteram seu comportamento (Sousa; Campos; Lima, 2007; Costa; Maia; Sampaio, 2012). Por outro lado, tal metodologia vem sendo pouco aplicada em estudos de previsão (Jarret; Kyper, 2011; Shi et al. 2012).

Outra alternativa metodológica é o uso de modelos Vetoriais Autorregressivos (VAR), que leva em conta a coexistência de relações de interdependência entre variáveis (Enders, 2004). Castro e Rossi Junior (2000) aplicaram modelos VAR irrestritos e modelos em diferença restritos para valores exportados das 11 principais commodities da pauta de exportações brasileira, identificando boa capacidade preditiva para as séries de soja. Ainda assim, verifica-se na literatura recente uma carência de estudos posteriores que corroborem tais apontamentos.

Posto isso, este presente estudo tem como objetivo avaliar a capacidade preditiva de modelos econométricos de séries temporais univariados e multivariados aplicados à previsão da série de valores mensais de exportação do complexo soja, avaliados em dólares. Para tanto, serão utilizados modelos ARIMA, de intervenção e vetoriais autorregressivos (VAR).

2. Metodologia

2.1. Modelos ARIMA (p, d, q)

  A abordagem Box-Jenkins (1976) de estimação de modelos ARIMA consiste na estimação da regressão da variável dependente em função das suas próprias defasagens, sendo p termos autorregressivos, e q termos da média móvel.

Os modelos ARIMA, por definição, requerem que as séries de dados sejam estacionárias, ou seja, se desenvolvam no tempo ao redor de uma média constante. Porém, também podem ser aplicados em séries de dados que contenham raiz unitária, desde que estas apresentem estacionaridade em um determinado grau d de diferenciação (Morettin; Toloi, 2006).  De maneira geral, o modelo ARIMA (p, d, q) pode ser escrito:

   ,  ~ (0,)       (1)

Em que Wt é a diferença da série temporal não estacionária Zt (; ),  é o termo aleatório com média zero e variância constante (), ,  e B o operador de translação para valores passados. Dessa forma, o modelo descrito em (1) supõe que a d-ésima diferença da série não estacionária Zt apresenta estacionaridade e pode ser representada por um modelo ARMA (p, q).

Conforme Box-Jenkins (1976), a construção destes modelos é baseada em um ciclo iterativo, no qual a escolha do modelo é feita com base na própria série em análise. As etapas do ciclo devem ser realizadas na ordem: (i) Especificação de uma classe geral de modelos; (ii) Identificação do modelo a ser estimado com base nas funções de autocorreção (FAC) e autocorrelação parciais (FACP); (iii) Estimação do modelo (parâmetros dos componentes autorregressivos, de médias móveis e as variâncias); (iv) Diagnóstico, que é a etapa onde se verifica o ajuste do modelo estimado aos dados, por meio da análise dos resíduos. Caso se verifique a inadequação do modelo, tal método sugere a volta à fase de identificação do ciclo.

2.2 Modelo de intervenção

O modelo de intervenção consiste em uma extensão natural da metodologia univariada, que permite que a série temporal da variável endógena seja influenciada por outras variáveis, como a ocorrência de um evento em um instante T conhecido a priori, possibilitando a incorporação e avaliação de seus impactos (Morettin; Toloi, 2006). Conforme Enders (2004), tal método é efetivo e útil para a realização de previsões quando a relação de causalidade é unidirecional.

Uma intervenção pode afetar a série temporal de várias maneiras, tendo como efeitos possíveis a mudança de nível, na direção ou na inclinação da série em estudo. De modo a captá-los, o método da análise de intervenção incorpora à estimação da classe de modelos do tipo ARIMA variáveis binárias (dummies) determinísticas, evidenciando-se efeitos de choques exógenos ocorridos em algum ponto pré-determinado do tempo sobre a variável de interesse (Morettin; Toloi, 2006).  Sendo T o instante da intervenção, existem dois tipos de binárias de intervenção: função degrau, em que ,  ou função impulso, em que , sendo a primeira de efeito permanente e a segunda, temporário (Morettin; Toloi, 2006). De maneira geral, o modelo pode ser descrito:

Em que  é a variável binária de intervenção;  são funções racionais da forma  em que  e  são polinômios em ,  é a defasagem no tempo para o início do efeito da j-ésima intervenção e  é a série residual, ou seja, a série temporal livre do efeito da intervenção. O processo de estimação segue-se da mesma maneira descrita para os modelos ARIMA.

2.3 Modelos Autorregressivos (VAR)

O uso de modelos VAR, proposto por Sims (1980), é uma alternativa aos modelos estruturais multiequacionais, que exigiam um grande número de restrições para identificação. A proposta do VAR convencional é considerada desejável essencialmente por estimar modelos irrestritos na forma reduzida, tratando todas as variáveis como endógenas (Enders, 2004). O procedimento de identificação do VAR, proposto por Sims (1980), ocorre por meio de um sistema recursivo para as relações contemporâneas entre as variáveis, que resultará em um sistema exatamente identificado. A imposição dessas restrições gerará uma decomposição dos resíduos que, dada nesta forma triangular, é chamada decomposição de Choleski (Enders, 2004).

Apesar de prática e funcional, esta forma mecânica de imposição de restrições tem como limitação a pouca fundamentação na teoria econômica. Tal problema é mitigado pelo uso do modelo VAR estrutural, proposto por Sims (1986) e Bernanke (1986). No entanto, segundo Enders (2004), o modelo de VAR estrutural, apesar de mais adequado às análises econômicas, geralmente é preterido com relação ao VAR convencional no contexto de aplicações em previsões, dado que não há interpretação estrutural dos erros de previsão de passos à frente, advindos de choques compostos pelos termos de erros estimados [5].

A formalização do modelo VAR convencional será baseada em Enders (2004). Considerando-se, por exemplo, um VAR bivariado de primeira ordem, com yt e zt estacionárias, e  e  ruídos brancos não autocorrelacionados que representam choques:

Dada a existência de efeitos contemporâneos entre as variáveis, diz-se que as equações não estão representadas na forma reduzida, o que pode ser obtido por meio de manipulações de álgebra matricial. Reescrevendo o sistema, temos uma representação na forma estrutural:

Com: ; ; ; ; e

Multiplicando-se por  é obtido o VAR padrão, ou:

Com: ;  e , por facilidade de notação. Enders (2004) define  como elemento i do vetor , e como  os elementos da matriz , de linha i e coluna j. Reescrevendo o sistema, temos o VAR na forma padrão:

Como os erros e1t, e2t são composições dos choques anteriores (ruídos brancos), pode-se demonstrar [6] que os erros apresentam média zero, variância constante e são serialmente não correlacionados. Assim, é possível estimar cada equação do VAR separadamente por meio do método dos mínimos quadrados ordinários (MQO), desde que o sistema seja identificado.      No presente estudo será utilizado o VAR convencional, com a decomposição dos resíduos na forma de Choleski a fim de obter a identificação do sistema. A partir disso, é necessário apenas selecionar a ordem adequada de entrada das variáveis, da menos para a mais endógena, devido à forma triangular inferior da matriz (Cavalcanti, 2010).

Para a definição do número ideal de defasagens a serem incluídas no modelo, deve-se pesar o número de variáveis e respectivos "lags" com a perda de graus de liberdade. Uma forma de definição é pela seleção dos modelos que apresentarem menores valores da generalização multivariada dos critérios de AIC e SBC [7]. No que diz respeito à previsão, deve ficar claro que representará uma extensão multivariada das previsões utilizando uma autorregressão simples, sendo feita de forma recursiva.

2.4 Teste de Raiz Unitária

Os procedimentos descritos nas subseções anteriores supõem a estacionariedade das séries, ou que ao menos apresentem não estacionariedade homogênea. Para verificação desta propriedade, este estudo utiliza Teste de Dickey-Fuller Aumentado – ADF (Dickey; Fuller, 1979), que testa a hipótese de existência de raiz unitária, considerando processos autorregressivos AR(p), de ordem de defasagem p definida pelo critério de informação de Akaike (AIC) [8]. Também foi testada a coexistência de raiz unitária e termos determinísticos, através das estatísticas  (valores críticos em Dickey e Fuller, 1981).

2.5 Teste de cointegração e Modelos de Correção de Erros (VEC)

Os testes de cointegração são aplicados para se verificar a existência de equilíbrio ou relacionamento de longo entre as séries econômicas. São aplicados em séries não estacionárias com a mesma ordem de integração, dado que a após a diferenciação das séries pode-se perder os elementos de equilíbrio de longo prazo entre as variáveis. Assim, para que o modelo seja bem especificado, essa informação perdida deve ser recuperada, o que é feito pela incorporação ao modelo de um vetor de correção do erro (ECM). O teste de cointegração aplicado no presente estudo foi o de Johansen (1988), por permitir testar a existência de mais de um vetor de cointegração.

2.6 Procedimento de comparação de modelos de previsão

O elemento crucial para a comparação entre múltiplas previsões é a função perda . Existem variadas funções perda utilizadas na estatística, como erro médio (EM), erro percentual médio (EPM), raiz do erro quadrático médio (REMQ), entre outras, sendo comumente utilizada na literatura a função de erro quadrático médio, representada por (Diebold; Lopez, 1996).

Dada a seleção da função perda a ser utilizada, deve-se analisar qual dos modelos a minimiza. A seleção pode ser feita a partir do simples ranqueamento. Alternativamente se pode testar a hipótese nula de que as diferenças entre os MSE não são estatisticamente significantes, ou mesmo incorporar medidas de variabilidade amostral à medida (Diebold; Lopez, 1996).

Neste estudo realizou-se o ordenamento simples dos MSE das previsões e a construção da estatística "U de Theil" (coeficiente de desigualdade) como medida de comparação de desempenho entre os modelos estimados. A estatística U busca comparar as acurácias da previsão do modelo selecionado com a de uma previsão "ingênua", sendo esta última representada por um passeio aleatório simples ou, como no presente estudo, pelo valor de origem das previsões repetidos em h (horizonte de previsão) passos a frente (Diebold; Lopez, 1996). Dessa forma, a medida é dada por   e os melhores modelos são aqueles cujas estatísticas mais se distanciam da unidade. As análises deste estudo foram realizadas para previsões fora da amostra, considerando o horizonte de previsão de seis meses (h=6).

3. Descrição dos dados

Foram utilizados neste estudo valores agregados de periodicidade mensal de exportação do complexo soja em dólares, no período de janeiro de 1995 a setembro de 2013, totalizando 225 valores observados para cada produto. Os dados foram obtidos da Secretaria de Comércio Exterior (SECEX), por meio da plataforma AliceWeb [9] e organizados pelo agrupamento de 13 códigos de produtos segundo a Nomenclatura Comum do Mercosul (NCM) em oito dígitos [10]. O complexo soja definido neste estudo engloba produtos básicos ou com algum grau de manufatura: soja em grãos, farelo de soja e óleo de soja. A opção por utilizar as séries de exportação em valores monetários (US$) traz como vantagem a possibilidade de construção de análises econômicas posteriores com relação aos impactos diretos em valores (US$) sobre a balança comercial brasileira e orientar estudos que busquem analisar a rentabilidade deste setor agroexportador. Essa alternativa é contrária à tradicionalmente encontrada na literatura, em que é mais frequente a ocorrência de estudos de séries do quantum exportado (Monteiro, 2012; Barros; Bacchi; Burniquist, 2002; Carvalho; Negri, 2000). Por outro lado, estudos anteriores verificaram bom ajuste a modelos para séries de exportação em valores monetários (Castro; Cavalcanti, 1997). 

Para a estimação do modelo VAR, também foram utilizados dados do índice de preços de exportação (IPE) da soja em grão (CEPEA, 2013), como proxy do índice do IPE do complexo soja; preço médio recebido pelo agricultor de 60kg em R$ de soja em grão (SEAB-PR, 2013), como proxy do preço doméstico recebido pelo produtor; Índice de Câmbio (CEPEA, 2013), que representa o índice real efetivo para o agronegócio; produto interno bruto em R$ milhões (BCB, 2013) [11]; e dados de importações mundiais em US$ bilhões (FMI, 2013), como proxy para a renda mundial.

As séries em US$ foram deflacionadas pelo índice de preços de preços ao consumidor urbano dos Estados Unidos, sem ajuste sazonal (Consumer Price Index for All Urban Consumers – CPI), disponibilizados pelo Federal Reserve Economic Data (2013). Já as séries em R$ foram deflacionadas pelo índice de preços ao consumidor geral (IPC) (FGV, 2013) [12], ambos para preços de setembro de 2013.

Importante observar que para a estimação dos modelos propostos neste estudo, foram utilizados apenas os dados de janeiro de 1995 a março de 2013, retirando-se seis observações da amostra, para que fosse possível a composição do critério de comparação das previsões dos modelos.  

Para a análise dos dados e realização de estimativas deste estudo foi utilizado o software R versão 2.15.2. (R Foundation For Statistical Computing, 2013).

4. Resultados e Discussão

Os resultados obtidos neste estudo são apresentados em três etapas. Na primeira foi feita uma análise inicial da série mensal de valor exportado do complexo soja (em US$), de janeiro de 1995 a março de 2013, de modo a se verificar estacionaridade e realizar os procedimentos para a obtenção da mesma. Na segunda etapa foram ajustados modelos utilizando as três diferentes abordagens metodológicas já descritas. Ao final é realizada a comparação dos modelos, utilizando-se as seis observações retiradas da amostra (dados de abril de 2013 a setembro de 2013) pelo critério de U-Theil e EQM mínimo.

4.1 Análise inicial e ajustes

A representação gráfica da série de valor exportado em US$ do complexo da soja (neste momento denominada de Yt) é apresentada na Figura 1 onde se observa a possível presença de componentes de sazonalidade e tendência, assim como de variabilidade não constante.

Figura 1 – Série mensal Yt no período de janeiro de 1995 a março de 2013

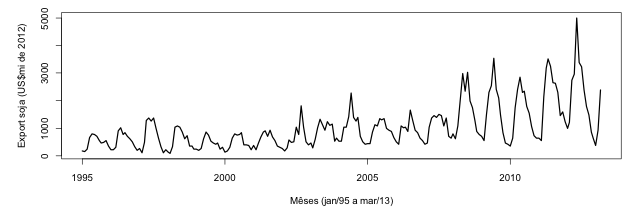
Para se verificar a necessidade de transformação dos dados para a estabilização da variância, a série foi dividida em subconjuntos de nove observações e para cada grupo foram calculados o desvio-padrão e a média. A análise da distribuição dos pontos indicou a necessidade de aplicação à série de uma transformação logarítmica (lnYt), conforme Box-Cox (1964).

Segundo Francisco et al (1995), as séries econômicas do setor agrícola comumente apresentam componentes sazonais, principalmente advindas das condições climáticas associadas às estações do ano. Neste presente estudo, a presença de sazonalidade determinística na série foi analisada por meio da construção de dummies sazonais. Conforme sugerido em Morettin e Toloi (2006), para a construção matriz de regressão tenha posto completo ():

A partir da série lnYt foi estimado um modelo de regressão incorporando estas variáveis dummies sazonais:

Sendo , onde, as dummies sazonais mensais, , onde , são os coeficientes dessas dummies e  é o intercepto. Dessa maneira,  corresponde à série "filtrada" dos efeitos sazonais.

Os coeficientes das dummies sazonais se mostraram significativos conjuntamente: dado o valor da estatística F (14,62), rejeita-se a hipótese nula, , indicando a presença de efeitos determinísticos sazonais.  

Na Tabela 2 apresenta-se o resultado do teste ADF de raiz unitária (DICKEY; Fuller, 1979). O número de defasagens da variável a ser incluídas no teste foi selecionado através do critério de informação de Akaike (AIC) e, dada a inexistência de tendência quadrática na série Zt, partiu-se do modelo inicial já mais restrito, que inclui apenas o drift (verificação de tendência linear na série em nível). Sobre o resíduo da regressão supracitada (εt), que representa o componente da série temporal livre dos efeitos sazonais determinísticos (agora denominado neste estudo por Zt). Verifica-se que não é possível rejeitar a hipótese nula de raiz unitária da série Zt em nível, obtendo-se estacionaridade após a primeira diferenciação, sendo I(1).

Tabela 1 - Resultados do teste ADF de raiz unitária

4.2 Modelo ARIMA (p, d, q)

A estimação do modelo ARIMA (p, d, q) seguiu o processo iterativo do método de Box e Jenkins (1976). Após a verificação de que a série é I(1), buscou-se identificar o processo ARIMA (p, d, q) resultante, por meio da análise das funções de autocorrelações (FAC) e autocorrelações parciais (FAC parcial) estimadas da primeira diferença da série Zt (Figura 2). Pela análise preliminar, foram selecionados na fase de identificação do processo iterativo três modelos candidatos: ARIMA (1, 1, 0), ARIMA (0, 1, 1) e ARIMA (1, 1, 1), respeitando-se o princípio da parcimônia. No momento da estimação do modelo ARIMA, utilizou-se a série , incorporando-se os regressores determinísticos de sazonalidade (dummies sazonais).

Figura 2 – FAC e FAC parcial da primeira diferença da série Zt

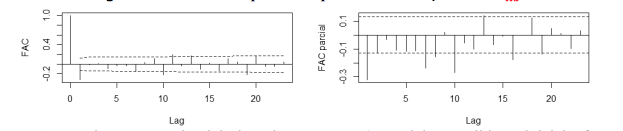
Ao seguir as etapas do ciclo iterativo com os três modelos candidatos iniciais, foram identificados respectivamente três modelos que apresentaram bom ajuste ao observar as FAC e FAC parcial residuais e significância por teste t dos coeficientes estimados:

(1) ARIMA (10, 1, 2) incompleto:

 ;

(2) ARIMA (13, 1, 1) incompleto:

 ;

(3) ARIMA (10, 1, 1) incompleto:

 ;

Na etapa de diagnóstico dos modelos, foram realizados testes de Ljung-Box (1978) para verificação de autocorrelação dos resíduos estimados e Shapiro-Wilk (Shapiro et al.,1968) para normalidade dos resíduos. Conforme os resultados apresentados na Figura 3, verificamos que os três modelos estimados apresentaram ausência de autocorrelação residual. Com relação à normalidade dos resíduos, verificamos pela Tabela 3, que a 5 % de significância apenas para o modelo (3) ARIMA(10[4,5,6,10],1,1) não podemos rejeitar a hipótese nula de normalidade dos resíduos. No caso de 1% de significância, podemos não rejeitar a hipótese de normalidade para os três modelos estimados.

Figura 3 - Resultado do teste de Ljung-Box (1978) para autocorrelação residual

----

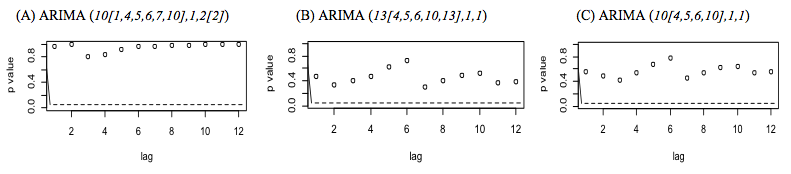
Tabela 2 – Teste de Shapiro-Wilk (1968) para normalidade dos resíduos

4.3 Modelos de Intervenção

As intervenções analisadas e adotadas nos modelos de intervenção estimados podem ser agrupadas em duas categorias: (1) Intervenções de preço; e (2) Intervenções Institucionais. Para a composição do primeiro grupo, foi analisada a evolução das cotações internacionais do complexo soja (Figura 4), onde verifica-se a presença de três expressivos picos de preço no período em questão. 

Figura 4 – Preços da soja (grão, farelo e óleo) em US$ – jan/1995 a mar/2013

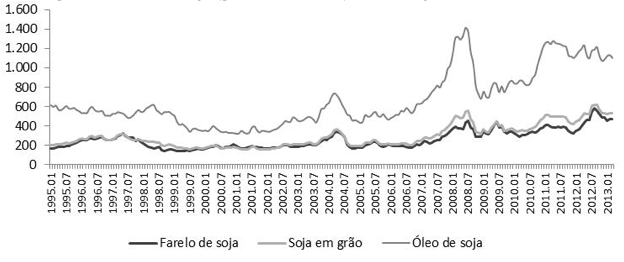
O primeiro choque positivo compreende o período que se inicia no segundo semestre de 2002 e termina ao final do primeiro semestre de 2004. Após 2001, observou-se tendência de crescimento mais pronunciado do PIB mundial [13] que foi acompanhada pelos preços dos produtos agrícolas no mercado global, dada a rigidez de oferta no curto e médio prazo destes produtos (Prates, 2007). Neste período, o boom de preços foi reforçado pelo estímulo da desvalorização cambial, resultando em um período de expressivo dinamismo para a agricultura brasileira de modo geral (Brandão; Rezende; Marques, 2006).

O segundo choque de preços teve início no segundo semestre de 2007. Neste período, aliada à pressão de demanda por grãos já existente, houve a crise financeira do subprime que incentivou a migração de fundos de investimentos dos ativos financeiros para o mercado futuro de commodities, impactando em expressiva alta das cotações dos cereais (Freitas, 2009). Já após agosto de 2008, iniciou-se a expectativa de recessão global, e a aversão ao risco trouxe a apreciação do dólar e queda nas cotações internacionais de commodities. O último movimento de preços destacado, que teve início em 2010 e perdurou até o final da série, está relacionado ao forte crescimento da demanda chinesa por soja em grão (Araújo; Gentil, 2011).  

O segundo grupo de intervenções analisado compreende duas mudanças institucionais citadas na literatura como responsáveis por impactos positivos no crescimento das exportações do complexo soja: a Lei Kandir (setembro de 1996) e a mudança do regime cambial, e consequente desvalorização do real, a partir de 1999 (Coronel et al., 2008; Cassuce; Santos, 2005). A Lei Kandir, com a desoneração as exportações de produtos in natura do Imposto sobre Circulação de Mercadorias (ICMS) impactou positivamente na exportação de soja em grão, mas, por outro lado, é reportado na literatura o impacto negativo na exportação de produtos que poderiam ter maior valor agregado, como farelo e óleo (Wilder; Martines Filho; Barros, 1999). Já a desvalorização cambial iniciada em 1999 gerou competitividade aos produtos brasileiros no mercado internacional.

Dado esse contexto, foram criadas cinco dummies representativas dos eventos citados, de modo a incorporar o efeito destes choques exógenos nos modelos ARIMA estimados na subseção anterior, modelos (1), (2) e (3):

Tabela 3 – Relação de variáveis dummies de intervenção

 Fonte: Elaborado pelos autores

No entanto, a análise de diagnóstico dos modelos com as dummies, incluídas tanto separadamente quanto combinadas, não mostrou significância dos coeficientes destas, com exceção do caso do primeiro choque de preços (di1), que apresentou impacto positivo significativo sobre o valor exportado de soja para os três modelos ARIMA em que foi incluído. No caso da desvalorização do real perante o dólar, ainda que à primeira vista devesse ter exercido impacto positivo sobre as exportações, a dummy de intervenção di5 não apresentou significância. Tal resultado corrobora o estudo de Brandão, Rezende e Marques (2006), que aborda a hipótese de que o efeito da depreciação do cambio pode ter sido parcialmente neutralizado por uma consistente queda dos preços internacionais da soja no mesmo período, conforme verificado na Figura 4.      

A Lei Kandir (di4) também não apresentou coeficiente significativo. Tal fato traz a evidência de que a desoneração de ICMS para produtos in natura, ainda que tenha exercido efeito imediato impulsionando as exportações de soja em grão, impactou secundariamente de forma negativa as exportações de farelo e óleo de soja. Outra justificativa a não significância do efeito da Lei relaciona-se ao período selecionado para análise no presente estudo, que se inicia no ano de 1995. Segundo Brandão, Rezende e Marques (2006), no biênio 1995-1996, os preços agrícolas internacionais de grãos e oleaginosas estavam em um elevado patamar, atingindo picos históricos e, após isso, em período coincidente com a instauração de Lei Kandir, os preços estavam em tendência de queda expressiva. Assim, foram selecionados mais três modelos preliminares, os estimados anteriormente com a inclusão da dummy para o primeiro choque de preços (Modelos com intervenção 1, 2 e 3).

4.4. Modelo VEC

Fundamentação teórica: estimação de funções de exportação

No contexto multivariado, para que seja possível fazer previsões das exportações do complexo soja, é preciso que seja estimada a função de exportação. A especificação do modelo adequado para tal é baseada nas teorias econômicas do consumidor e da firma e pode assumir três hipóteses distintas, de acordo com Barros, Bacchi e Burniquist (2002): (1) país pequeno tomador dos preços internacionais: modelo analítico considera apenas a função de oferta de exportação; (2) perfeita elasticidade da oferta de exportação: modelo analítico baseado na função de demanda; (3) elasticidade finita tanto para oferta quanto para a demanda: considera o efeito simultâneo das variáveis de oferta e de demanda no modelo. Outro aspecto a ser considerado é o grau de substituição do produto. Mesmo no caso de commodities, que apresentam certa homogeneidade, é comum na literatura a suposição de substituição imperfeita, visto que a substituição perfeita em mercados competitivos com custos marginais constantes implicaria dominância de um dos mercados (doméstico ou externo) e elasticidade infinita (Barros; Bacchi; Burniquist, 2002).

O presente estudo trabalha no cenário da terceira hipótese, com substituição imperfeita, por meio de uma função de exportação na forma uniequacional, incluindo variáveis relacionadas à oferta e à demanda na mesma equação, conforme utilizado por Castro e Cavalcanti (1997) e Cavalcanti e Ribeiro (1998) para exportações nacionais, e em Carvalho e Negri (2000), Barros, Bacchi e Burnquist (2002), Alves e Bacchi (2004), Silva e Bacchi (2005) no contexto agropecuário.

Modelo econômico proposto

A estimação uniequacional se baseou em Miranda (2001) e Silva e Bacchi (2005). Estes estudos assumem que a oferta de exportação é expressa como excesso de oferta em relação à demanda doméstica. Sendo a oferta e a demanda no mercado doméstico, funções:

 Onde  é a oferta e  a demanda do produto no mercado interno (R$),  o preço doméstico (R$),  o preço de exportação (R$),  um deslocador da oferta doméstica, e  um deslocador da demanda doméstica. Então a oferta de exportação, pode ser representada:

Já a demanda por exportação é dada por: sendo: a oferta de exportação convertida em US$ pela taxa cambial,  a demanda de exportação brasileira no mercado externo (US$),  o preço de exportação (US$),  um deslocador de demanda internacional. Considerando o equilíbrio no mercado externo, , com  representando o valor de equilíbrio negociado no mercado externo, ou, exportações do Brasil, tem-se que: , onde  e é a taxa cambial.

O deslocador de oferta doméstica, conforme Miranda (2001), pode ser representado por uma variável tendência, que busca captar efeitos de avanços tecnológicos, e também componentes sazonais da oferta de soja.  O deslocador de demanda doméstica será a renda nacional e o deslocador de demanda externa a renda mundial

Estimação Modelo VEC

Para estimação do VEC, foram consideradas as variáveis: Preço internacional da soja em grão (Px), preço doméstico da soja (Pd), índice de câmbio (IC), PIB nacional (PIB) e importações mundiais totais (IMPm), todas utilizadas em transformação logarítmica, além da série lnYt. Foi verificada a estacionariedade das séries por meio do teste ADF, conforme resultados apresentados na tabela 5. Verifica-se que todas as séries apresentam raiz unitária, sendo estacionárias após a primeira diferença, I(1). Assim o modelo será estimado com as séries na primeira diferença.

Tabela 4 – Resultados do teste ADF de raiz unitária

Fonte: elaborado pelos autores
* Modelo 2 refere-se a aplicação do teste de ADF, modelo mais restrito, na série em primeira diferença
** Para a série PIB o modelo 2 incorpora o termo drift, não estando na forma mais restrita (φ1=48.54)
*** Valores críticos de Dickey e Fuller (1981) a 1% de significância

Sendo todas as séries I(1), foi testada a presença de cointegração por meio do procedimento de Johansen (1988), conforme os resultados da tabela 5. Verificou-se, a 1% de significância, a existência de um vetor de cointegração, de modo que o modelo será estimado na forma de correção do erro.

Tabela 5 – Resultados do teste de Cointegração (JOHANSEN, 1988)

Fonte: elaborado pelos autores
*Valores críticos de λtrace em MacKinnon, Haug e Michelis (1999).

Para estimação do VEC, foi considerado defasagem de cinco meses. Optou-se por este número de defasagens ainda que divergisse do indicado pelo critério de informação de AIC (três defasagens). Tal escolha justifica-se pelo critério de comparação de modelos de previsão adotado no estudo, que busca modelos com menor EQM. Na equação referente à variável de interesse deste estudo (dlnYt) [14], se mostraram significativos os impactos de dlnIMPm (defasagens  1, 3 e 5), dlnPIB (defasagens 1 e 5),  dlnIC (defasagem 3), dlnPx (defasagem 4) e dlnPd (defasagem 5). Os deslocadores de oferta, efeito sazonal e constante, que representa a tendência linear na série em nível, foram significativos. Os gráficos da figura 5 indicam a regularidade do modelo, ou seja, bom ajuste do modelo aos dados, estacionariedade dos resíduos e não existência de autocorrelação residual para a série de interesse deste estudo.

Figura 5 – Diagramas de ajuste, resíduo e FAC e FAC parcial residuais do dlnYt

4.5. Comparação das previsões dos modelos estimados

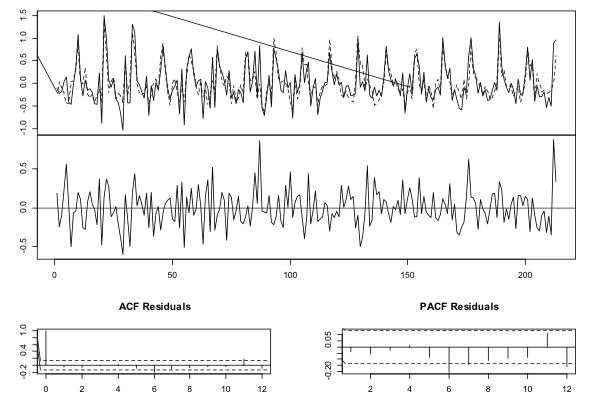
Para o cálculo do erro médio de previsão, foram retiradas seis observações de cada série e, então, realizadas previsões seis passos à frente por meio dos modelos estimados selecionados em cada metodologia. Os valores reais foram comparados com os previstos para o cálculo do EQM, que foi utilizado na construção da estatística U-Theil em conjunto com o EQM da previsão ingênua (repetição seis passos a frente do valor de origem das previsões).  A tabela 7 sumariza os resultados obtidos:

Tabela 6 – Resultados do EQM e U-Theil dos modelos

A comparação dos valores previstos de EQM mínimo de cada classe de modelos e o valor real da série é apresentada na Figura6.

Figura 6 – Valores previstos (modelo 3, modelo 3 com intervenção e VEC) e valores reais

5. Conclusões

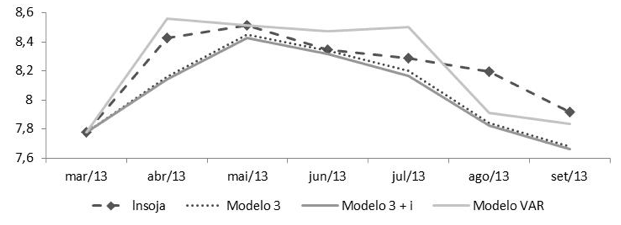
Com este estudo empírico, pôde-se comparar os resultados dos modelos univariados e multivariados de séries temporais aplicados à previsão da série de valor exportado de soja em dólares, de forma a se avaliar as diferenças na capacidade preditiva de cada modelo.

A partir dos resultados obtidos, verifica-se que o melhor ajuste derivou-se do modelo VEC, indicando que inclusão de variáveis que se inter-relacionam com a variável de interesse, aumenta a capacidade de previsão, no que diz respeito ao horizonte adotado neste estudo (seis meses).

Em sequência ao modelo VEC, vieram os resultados dos modelos da classe ARIMA, quando comparados às suas respectivas variantes com a adição da intervenção. Cabe destacar que, considerando-se a estatística U-Theil pode-se concluir que todos os modelos ARIMA selecionados apresentaram bons resultados, com os valores das estatísticas notoriamente inferiores a uma unidade.

Paralelamente, as intervenções analisadas e representadas por meio de dummies não foram, em sua maioria, significativas. Apenas um único choque de preços mostrou-se significativo, mas suas previsões mostraram-se menos eficientes que os modelos ARIMA sem intervenção, conforme o critério de comparação de U-Theil. Recomenda-se, neste aspecto a estudos vindouros que busquem analisar o efeito de intervenções com maior profundidade, possivelmente compreendendo um horizonte de tempo maior à série de valor exportado de soja em US$ analisada.

A formação de preços das commodities agrícolas é influenciada pelas variações que ocorrem no mercado internacional devido à comercialização mundial, por isso, os elementos discutidos e avaliados neste estudo trazem reflexões que balizam futuras pesquisas na área, sendo sempre importante compreender os limites deste tipo de investigação, quanto ao período de análise empregado e aos métodos utilizados.

Outras abordagens poderiam ter sido aplicadas e possivelmente com bom ajuste, como os modelos univariados de suavização exponencial ou de espaço de estados. Dada a importância deste tipo de previsão para a estruturação de estratégias e planejamento da agroindústria do complexo soja no contexto mundial, sugere-se a realização de estudos futuros que contemplem de modo dinâmico estes e outros aspectos, que subsidiem o processo de formulação, implementação e avaliação de políticas econômicas.

6. Referências

ALVES, L. R. A.; BACCHI, M. R. P. (2004); "Oferta de Exportação de Açúcar do Brasil", Revista de Economia e Sociologia Rural, 42(1), 09-33.

ARAÚJO, V. L., GENTIL, D. L. (2011); "Avanços, recuos, acertos e erros: uma análise da resposta da política econômica brasileira à crise financeira internacional", Texto para discussão n. 1602, IPEA, 39 p.

ASSOCIAÇÃO BRASILEIRA DAS INDÚSTRIAS DE ÓLEOS VEGETAIS (ABIOVE). (2013); "Arquivo com Estatística Mensal de Exportação", Disponível em: < http://www.abiove.org.br/site/index.php?page=estatistica&area=NC0yLTE=> Acesso em: 13 dez. 2013. 

BANCO MUNDIAL. (2010); "Rising global interest in farmland: can it yield sustainable and equitable benefits", Washington D. C. 2010. Disponível em <http://siteresources.worldbank.org/INTARD/Resources/ESW_Sept7_final_final.pdf>. Acesso em: 9 dez. 2013.

BARROS, G. S. C., BACCHI, M. R. P., BURNQUIST, H. L. (2002); Estimação de equações de oferta de exportação de produtos agropecuários para o Brasil (1992/2000), Texto para discussão n. 865, IPEA, 51 p.

BERNANKE, B. (1986); "Alternative explanations of money-income correlation." Carnegie-Rochester Conference Series on Public Policy, 25, 49-100.

BLACK, C. (2013); "Eventos relacionados ao superciclo de preços das commodities no século XXI", Indicadores Economicos FEE, 40(2), 67-78

BOX, G. E. P.; JENKINS, G. M. (1976); "Time series analysis: forecasting and control", San Francisco: Holden-day.

BOX, G. E. P.; COX, D. A. (1976); "Distribution of autocorrelations in autoregressive moving avarege time series models", Journal of the American Statistical Association, 65(332), 1509-1526.

BRANDÃO, A. S. P., REZENDE, G. C., MARQUES, R. W. C. M. (2006); "Crescimento agrícola no período 1999-2004: a explosão da soja e da pecuária bovina e seu impacto sobre o meio ambiente", Economia Aplicada, 10(2), 249-266

BRASIL. (2012); Ministério Da Agricultura, Pecuária E Abastecimento (MAPA), Assessoria de Gestão Estratégica. Brasil projeções do agronegócio 2011/2012 a 2021/2022. Brasília.

BRASIL. (2013); Ministério do desenvolvimento, indústria e comércio exterior (MDIC). Balança Comercial Brasileira: Dados Consolidados, Janeiro a Junho de 2013. Brasília, 2013.

BRASIL. (2013); Ministério do desenvolvimento, indústria e comércio exterior (MDIC). Sistema de Análise de Informações de Comércio Exterior – Aliceweb. Disponível em: <http://aliceweb2.mdic.gov.br/> Acesso em: 20 nov. 2013.

CARVALHO, A; NEGRI, J. (2000); A Estimação de equações de importação e exportação de produtos agropecuários para o Brasil (1977/1998), Texto para Discussão n.698, IPEA. Brasília 30 p.

CASSUCE, F. C. C.; SANTOS, M. L. (2005); "Desvalorizações cambiais e captação de divisas: o caso brasileiro da produção de soja em grão", Revista Organizações Rurais e Agroindústrias. 7(3), 298-311.

CASTRO, A. S. de.; CAVALCANTI, M. A. F. H. (1997); Estimação de Equações de Exportação e Importação para o Brasil – 1955/1995. Texto para Discussão n. 469. IPEA. Rio de Janeiro, 30 p.

CASTRO, A. S.; ROSSI JUNIOR, J. L. (2000); Modelos de previsão para a exportação das principais commodities brasileiras, Texto para Discussão n. 716. IPEA. Brasília, 35p.

CAVALCANTI, M. A. F. H.; RIBEIRO, F. (1998); As exportações brasileiras no período 1977/96: Desempenho e determinantes. Textos para discussão n. 545. IPEA. Rio de Janeiro.

CAVALCANTI, M. A. F. H. (2010); "Identificação de modelos VAR e causalidade de Granger: uma nota de advertência", Economia Aplicada,14(2), 251-260.

CENTRO DE ESTUDOS AVANÇADOS EM ECONOMIA APLICADA (CEPEA). (2013); Índice de Preços de Exportação do Agronegócio Brasileiro.

COSTA, C. K. F.; MAIA, S. F.; SAMPAIO, L. M. B. (2012); "Exportações Brasileiras de Suco de Laranja e Subsídios Americanos: uma análise empírica de estratégias comerciais (1991-2006)", Revista Economia e Sociologia Rural,50(1), 083-106.

CORONEL, D. A.; MACHADO, J. A. D.; CARVALHO, F. M. A.(2008); "Fontes de crescimento das exportações do complexo soja brasileiro (1995-2004)" Revista de Economia e Administração, 7, 481-501.

DICKEY, D. A.; FULLER, W. A. (1979); "Distribution of the estimator for auto-regressive time series with a unit root", Jornal of the American Statistical Association,74(366), 427-431.

DICKEY, D. A.; FULLER, W. A. (1981); "Likelihood ratio statistics for auto-regressive time series with a unit root." Econometrica,49 (4), 1057-1072.  

DIEBOLD, F. X.; LOPEZ, J. A. (1995); Forecast evaluation and combination. Research Paper n. 9525. Federal Reserve Bank of New York. 1995.

ENDERS, W. (2004); Applied Econometric Time Series. 2nd ed. New York: Wiley, 544 p.

FEDERAL RESERVE ECONOMIC DATA (FRED). (2013); Consumer Price Index for All Urban Consumers: All Items (USA Inflation). St. Louis FED.

FRANCISCO, V. L. F. S.; PINO, F. A.; SUEYOSHI, M. L. S.; CÉZAR, S. A. G.; AMARAL, A. M. P. (1995); "Sazonalidade em séries temporais econômicas: aplicações". Agricultura em São Paulo. 42(1), 57-71.

FREITAS, M. C. P. (2009);  "Inflação mundial e preços de commodities". In: BIASOTO JUNIOR G.; NOVAIS L. F.; FREITAS M. C. P. (Org.). Panorama das Economias Internacional e Brasileira: dinâmicas e impactos da crise global. Fundap.1 (1), 113-124.

FUNDO MONETÁRIO INTERNACIONAL (FMI). (2013); World Economic Outlook Database. Disponível em: <http://www.imf.org/external/data.htm>. Acesso em 9 dez. 2013.

HIRAKURI, M. H.; LAZZAROTTO, J. J. (2011); Evolução e perspectivas de desempenho econômico associadas com a produção de soja nos contextos mundial e brasileiro. Embrapa Soja, Documentos, 319.

JARRETT, J. E.; KYPER, E. ARIMA (2011); "Modeling with intervention to forecast and analyze chinese stock prices", International Journal of Engineering Business Management. 3(3), 53-58.

JOHANSEN, S. (1988); "Statistical analysis of cointegration vectors", Journal of Economics Dynamics and  Control, 12, 231-254.

LJUNG, G. M.; BOX G. E. P. (1978); "On a measure of fit in time series models", Biometrica, 65(2), 297-303.

MACKINNON, J. G.; HAUG, A. A.; MICHELIS, L. (1999); "Numerical distribution functions of likelihood ratio tests for cointegration", Journal of Applied Econometrics, 14(5), 563-577.

MIRANDA, S. H. G. (2001); Quantificação dos efeitos das barreiras não-tarifárias sobre as exportações brasileiras de carne bovina. Tese (Doutorado em Ciências). Área de concentração: Economia Aplicada. Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo, Piracicaba.

MONTEIRO, E. Z. (2012); "Exportações de café do espírito santo: aplicação da metodologia VAR", Revista de Política Agrícola, 21(4), 106-119.

MORETTIN, P. A.; TOLOI, C. M. C. (2006); Previsão de séries temporais, Edgard Blücher. São Paulo, 2, 564 p.

PRATES, D. M. (2007); "A alta recente dos preços das commodities", Revista de Economia Política, 27(3),323-344.

R FOUNDATION FOR STATISTICAL COMPUTING. (2013); R: A Language and Environment for Statistical Computing 2.15.2. Disponível em: <http://www.R-project.org>. Acesso em 9 dezembro 2013.

SHAPIRO, S. S., WILK, M. B.; CHEN, H. J. (1968); "A Comparative Study of

Various Tests for Normality", Journal of the American Statistical Association, 63, 1343–1372.

SHI, H; ZHANG, X.; SU, X; CHEN, Z. (2012); "Trend Prediction of FDI Based on the Intervention Model and ARIMA-GARCH-M Model", AASRI Procedia, 3, 387-393.

SECRETARIA DA AGRICULTURA E DO ABASTECIMENTO DO PARANÁ (SEAB-PR). (2013); Preços recebidos pelo produtor (mensal). Disponível em: <http://www.agricultura.pr.gov.br/modules/conteudo/conteudo.php?conteudo=195> . Acesso em 9 dezembro de 2013.  

SIM, C. (1980); "Macroeconomic and reality", Econometrica, 48, 1-49.

SILVA, M. V. S. E. ; BACCHI, M. R. P. (2005) "Condicionantes das exportações brasileiras de açúcar bruto" Agricultura em São Paulo, 52 (2), 99-110.

SOUSA, E. P.; CAMPOS, A. C.; LIMA, J. E.(2007); "Análise de intervenção aplicada às exportações brasileiras de melão" Poster. XLV congresso da sociedade Brasileira de Economia, Administração e Sociologia Rural (SOBER). Londrina.

VERÍSSIMO, M. P.; XAVIER, C. L.; VIEIRA, F. V. (2012); "Taxa de câmbio e preços de commodities: uma investigação sobre a hipótese da doença holandesa no Brasil",EconomiA. 13(1), 93-130.

1.Escola Superior de Agricultura "Luiz de Queiroz". Universidade de São Paulo (USP). renno.nicole@gmail.com
2. Escola Superior de Agricultura "Luiz de Queiroz". Universidade de São Paulo (USP). lgilio@usp.br
3. Centro de Estudos Avançados em Economia Aplicada (CEPEA/USP). adrianaufv@hotmail.com
4. Escola Superior de Agricultura "Luiz de Queiroz". Universidade de São Paulo (USP). vaozaki@usp.br
5. Para uma descrição formal detalhada, ver Enders (2004).
6. Para uma descrição formal detalhada, ver Enders (2004).
7. ; (ENDERS, 2004).
8. Implica na seleção do menor valor para o critério, que é definido por: , com n sendo o número de parâmetros, T o número de observações e SSR a soma dos quadrados dos resíduos (ENDERS, 2004).
9. Disponível em: <http://aliceweb2.mdic.gov.br/> acesso em 9 de dezembro de 2013.
10. Códigos NCN de oito dígitos agrupados como "complexo soja": (1) Grupo "soja em grão": 12010010, 12010090,12011000,12019000; (2) Grupo " farelo de soja": 23040010, 23040090, 12081000, 35040020; (3) Grupo  "óleo de soja": 15071000,15079010,15079011,15079019,15079090 (SECEX,2013)
11. Referência primária para a obtenção desta variável foi o sistema IPEADATA (http://www.ipeadata.gov.br/). Acesso em 9 dez. 2013. A fonte original foi o Banco Central do Brasil (BCB).
12. Referência primária para a obtenção desta variável foi o sistema IPEADATA (http://www.ipeadata.gov.br/). Acesso em 9 dez. 2013. A fonte original é a Fundação Getúlio Vargas (FGV/Conj. Econ. – IGP).
13. Entre 1995 e 2001 o PIB per capta mundial cresceu em média 1,3% a.a, já entre 2002 e 2004 o crescimento anual foi em média 8,4%a.a (WDI, 2013).
14. O uso da letra "d" na nomenclatura das variáveis indica, neste estudo, a primeira diferença.