Espacios. Vol. 36 (Nº 22) Año 2015. Pág. E-1

O Infinito em algumas considerações: Zenão, Kant e Borges

The Infinite In Some considerations: Zeno, Kant and Borges

Antonio Sérgio COBIANCHI 1

Recibido: 17/07/2015 • Aprobado: 15/08/2015

Contenido

1. Introdução

2. Considerações sobre alguns dos Paradoxos de Zenão

3. O Infinito com Relação ao Tempo e Espaço na Primeira Antinonia de Kant

4. Borges e o Paradoxo de Aquiles e a Tartaruga

5. Conclusão

6. Bibliografia

1. Introdução

O infinito um assunto sempre muito abordado por matemáticos, educadores matemáticos, físicos, filósofos, religiosos e escritores. Observa-se também que esse tema povoa a imaginação de pessoas que não estão ligadas diretamente ao meio científico ou literário. Esse interesse pelo infinito não é um fato atual, pois é constatado desde a Grécia Clássica, ou talvez na matemática dos babilônios.

Esse conceito além da Matemática, também se manifesta na física, literatura, religião e na filosofia. Na atualidade (Morris, 1998, p. 13) encontramos a ideia de infinito, proposta pelos filósofos estóicos [2] da Antiguidade, de que o universo está destinado a atravessar um número infinito de ciclos, e que os mesmos eventos se repetirão um número infinito de vezes. O infinito transpassou todas as etapas da história do mundo, e para a Matemática, destacando o infinito relacionado com o conjunto numérico dos números reais de interesse imediato para matemáticos e educadores matemáticos, o problema foi resolvido formalmente por Richard Dedekind [3] (1831-1916) e outros contemporâneos, somente em 1872.

Na geometria o infinito surge como processo de aproximação de um limite. A área do círculo é o limite para o qual tendem as áreas dos polígonos regulares inscritos ou circunscritos, no caso em que se aumente indefinidamente o número de lados. Diz-se, nesta situação, que o número de lados dos polígonos inscritos ou circunscritos tende ao infinito. A circunferência pode ser pensada como um polígono com infinitos lados, cada um deles infinitamente pequeno. Neste caso, o infinito não é somente um processo de cálculo, mas, antes, o resultado desse processo. É o número que está no fim da sequência de números, o limite dos valores numéricos sucessivos de uma variável que aumenta (ou diminui) a cada etapa.

Mas, apesar de toda a evolução humana (Morris, 1998, p. 11-12), o infinito é hoje algo tão desconcertante quanto no tempo de Aristóteles [4], sendo que a única diferença é que, ao perscrutar profundamente a natureza do universo, os cientistas vislumbram o infinito por procedimentos desconhecidos aos antigos gregos. Na linguagem cotidiana a palavra infinito, continua sendo usada como sinônimo de o que está além da compreensão humana. Mas quando encontrada em um contexto científico ou filosófico, o infinito não pode ser evitado com tanta habilidade ou facilidade.

Embora possa parecer paradoxal associar o nome escritor Jorge Luis Borges [5] (1899-1986) ao infinito, ele o abordou e esteve fascinado com o mesmo. Esse interesse pode ser observado em muitos de seus ensaios como Aleph, Contos de Areia, Avatares da Tartaruga, A Perpétua Corrida de Aquiles e a Tartaruga, entre outros. Afirma Borges, (1999, p. 175) que esse conceito é o corruptor e o desatinador de todos os outros: Não falo do Mal cujo limitado império é a ética; falo do infinito. Eu desejei compilar alguma vez sua móvel história. A numerosa Hidra (monstro palustre que vem a ser uma prefiguração ou um emblema das progressões geométricas)...

Borges (1999, p. 186) sugeriu que os confrontos com a infinidade, nos convencem do caráter alucinatório do mundo, e que devemos buscar irrealidades que confirmem esse caráter em situações que nenhum idealista [6] observou, como na dialética de Zenão [7] e nas antinomias [8] de Kant [9], elementos que perseguimos para a execução desse estudo. Somente por esta afirmação de Borges, observamos o quanto é instigador este tema, essa junção da Matemática, da Filosofia, Religião e da Literatura, gerando uma série interminável de indagações e suposições.

Nesse artigo detalhamos alguns dos paradoxos de Zenão, a primeira antinomia de Kant e opiniões de alguns dos estudiosos de Kant. Abordaremos elementos tratados no ensaio de Borges, Avatares da Tartaruga, publicado na sua obra Discusión. Tanto em Zenão como em Kant ou no ensaio de Borges, o infinito se apresenta em situações que envolvem o tempo e o espaço, temas fundamentais e delicados para as ciências exatas e também em alguns campos da Filosofia.

2. Considerações sobre alguns dos Paradoxos de Zenão

Com o objetivo de acercarmos mais dessa ideia do infinito, faremos alguns comentários sobre o pensamento de Zenão. Inicialmente acrescentaremos alguns elementos matemáticos e filosóficos sobre o infinito, para um melhor entendimento dos paradoxos de Zenão.

A Matemática trata com dois tipos diferentes de atividades, com relações estreitas com o infinito. A primeira envolve contagem de elementos discretos, separados e indivisíveis (como bolinhas de gude). A segunda relaciona medidas de quantidades que são contínuas e, na imaginação, infinitamente divisíveis, isto é, divisíveis sem fim. Essas duas operações estão juntas, pois se utiliza a contagem de números para a medição. Dois tipos de quantidades com as quais a Matemática costuma tratar e que tem produzido a maioria dos modelos são o espaço e o tempo. A Escola Pitagórica tinha assumido que o espaço e o tempo podem ser pensados como consistindo de pontos e instantes; mas o espaço e o tempo possuem também uma propriedade, mais fácil de intuir do que de definir, que é a continuidade, elemento relacionado ao infinito. (COBIANCHI, 2001, p.89-100)

Zenão, um discípulo de Parmênides [10], foi um dos primeiros filósofos antigos a examinar e se aproximar do conceito do infinito e, utilizou-se do tempo e do espaço, no seu ataque à construção pitagórica das mônadas, que para eles era o indivisível. Zenão afirmava que a realidade era uma unidade imutável, a que chamava de Um (COBIANCHI, 2001, p. 90). Para Parmênides (Giles, 1979, p. 8), o movimento, a mudança, a multiplicidade eram ilusões, e os que acreditavam na sua realidade estavam sendo enganados pelos seus sentidos. Sustentava que a realidade é um todo indivisível, contínuo, homogêneo e imutável e que, consequentemente, apesar de todas as aparências e de toda a experiência sensível, o movimento é apenas aparência ou ilusão. Ele acreditava que o pensamento racional podia desvendar a verdadeira natureza da realidade; não estava seguindo nenhuma senda espiritual. (MORRIS, 1998, p. 23)

Segundo Kline (1972, p. 35), foi Zenão quem deu relevância ao problema da relação entre o discreto e o contínuo. Essa relação gerou uma violenta polêmica e dela restaram, conservados por Aristóteles, alguns argumentos de Zenão:

Como querem que a reta seja formada por corpúsculos materiais de extensão não nula? Isso vai contra a vossa afirmação fundamental de que todas as coisas têm um número. Com efeito, entre dois corpúsculos, 1 e 2, deve haver um espaço - se estivessem unidos, em que se distinguiam um do outro? - e esse espaço deve ser maior que as dimensões de um corpúsculo, visto que estas são as menores concebíveis; logo, entre os dois posso intercalar um corpúsculo, 3, e fico com dois espaços: um entre 1 e 3, e outro entre 3 e 2, nas mesmas condições. Posso repetir o raciocínio indefinidamente e fico portanto, com a possibilidade de colocar entre 1 e 2 quantos corpúsculos quiser. Qual é então o número que pertence ao segmento que vai de 1 a 2?

(Aristóteles, in Caraça, 1997, p. 77-78)

Nesta época já aparece a ideia de infinito potencial e infinito atual. Abbagnano (1999, p. 562-563) afirma o infinito potencial como limite de certas operações sobre as grandezas, e o atual, como uma espécie particular de grandeza. O conceito do infinito potencial foi elaborado por Aristóteles, que negava o infinito atual, tanto como realidade em si (substância) quanto como atributo de uma realidade. Somente a Matemática moderna deu um conceito rigoroso de infinito atual, através das discussões tradicionais sobre os denominados paradoxos do infinito. Radice deu para esses infinitos, as seguintes definições:

infinito potencial, para uma sucessão de elementos, é a possibilidade de ir sempre mais longe, sem que se atinja um elemento último. ... Um infinito em ato, portanto, e não apenas em potência é uma infinidade realizada, e não apenas não completável; esgotada e não unicamente inesgotável. Uma sucessão infinita discreta, sempre reconduzível à repetição infinita de "mais outro", constitui um objetivo mental de todo o repouso.
(Radice, 1981, p. 8-10)

Costa opina sobre esses infinitos:

Para muitos matemáticos, só se pode conceber o infinito como essencialmente potencial e inatingível; um conjunto infinito não nos é dado presentemente com todos os seus elementos; o que nos nossos raciocínios define um tal conjunto é a possibilidade de obtermos sucessivamente quantos quisermos dos seus elementos. Os matemáticos da escola cantoriana aceitam, ao contrário, além desse infinito potencial, o infinito atual ou realizado. Para eles, um segmento de reta é uma totalidade atualmente dada de pontos, e não apenas pontos que se obtém um a um.
(Costa, 1981, p. 251)

A idéia de Aristóteles, sobre números em processo de diminuição ou aumento estava vinculada com o infinito potencial:

O número, em um processo de diminuição na direção ao mínimo, tem um final, enquanto que, em um processo de aumento, sempre se observa excedida qualquer quantidade que se tome. Nas grandezas ocorre o contrário: em um processo que tenda ao mínimo, fica excedida negativamente toda grandeza, enquanto que em um processo de aumento, não existe uma grandeza infinita. O motivo está em que o ser uno é um ser individual e indivisível, qualquer que seja o ser uno, como por exemplo, o homem é somente um homem e não muitos. E o número é várias vezes o uno e uma quantidade determinada. Onde é necessário que se pare no indivíduo. Pois o dois e o três são "parônimos", ou nomes derivados, e o mesmo qualquer outro número. Com efeito, no processo em direção ao mais, o número é sempre inteligível: já que a grandeza se pode dividir indefinidamente pela metade. Por esta razão, existe o infinito potencial, porem de nenhuma maneira o atual.
(Aristotle, 1996, p. 75, tradução livre)

O desenvolvimento dos argumentos de Zenão pode ser visto sob dois pontos de vista. No primeiro, o tempo e o espaço são infinitamente divisíveis, isto é, divisíveis sem fim. No segundo, existe um menor elemento indivisível de tempo, um instante, e de espaço, um ponto. Na opinião de Kline (1972, p. 35), o propósito de Zenão em relação aos seus paradoxos não é claro, por não ser suficiente o conhecimento que se possui da História da filosofia grega.

Em dois paradoxos, a dicotomia e Aquiles, Zenão argumentou que se o tempo e o espaço são infinitamente divisíveis, o movimento seria impossível. No paradoxo da dicotomia, para alcançarmos , saindo de , é necessário alcançar , que é o ponto médio entre  e . Para alcançar  é necessário alcançar , ponto médio entre  e . E para alcançar  é necessário alcançar , ponto médio entre  e . O argumento continua ad infinitum, concluindo-se então que o movimento não pode começar. No paradoxo de Aquiles e a Tartaruga, o argumento é semelhante. Se a tartaruga está em  e Aquiles em , Aquiles nunca alcança a tartaruga, pois no momento em que Aquiles chega em  a tartaruga estará em algum ponto  adiante, e quando Aquiles chega em  a tartaruga estará em algum ponto  adiante, e assim por diante ad infinitum, e a tartaruga estará sempre à frente. O paradoxo de Aquiles e a Tartaruga é um dos primeiros e mais famosos usos da idéia de infinidade. Afirma Morris (1997, p. 22), que é claro que Aquiles iria alcançar a tartaruga com muita facilidade. O que ele está dizendo é que Aquiles deve efetuar uma série infinita de atos, algo que não pode ser feito em um período de tempo finito.

No paradoxo da flecha Zenão adota a hipótese alternativa de que o tempo e o espaço não são infinitamente divisíveis, isto é, existe uma menor unidade indivisível de tempo, um instante; e de espaço, um ponto. Zenão considera uma flecha e diz que a flecha deve estar em um certo ponto em um dado instante. Como ela não pode estar em dois lugares no mesmo instante, não pode se mover naquele instante; se, por outro lado, está em repouso naquele instante, então, como o mesmo argumento se aplica para outros instantes, ela não pode se mover.

Desta circunstância surge um impasse, pois ambas as hipóteses, aparentemente alternativas corretas, levam a conclusões que parecem contrariar o bom senso; porque pode haver movimento, e Aquiles pode alcançar a tartaruga. Mas é uma situação em que alguma coisa deve ser rejeitada, ou o conceito de divisibilidade ad infinitum e sua alternativa aparente, a existência de indivisíveis em espaço e tempo, ou o conceito de movimento no mundo exterior, ou ainda o processo de dedução através do qual se tiram conclusões.

Os paradoxos de Aquiles e da flecha, se devem à confusão de dois aspectos bem diferentes de um problema particular. Ou se olha o fluxo contínuo do movimento ou se pensa nos objetos: a flecha, a tartaruga e Aquiles, ocupando várias posições ao longo de seu movimento. No último caso, é-se levado a fixar o objeto em determinado ponto, paralisando-se por um instante. As duas maneiras de encarar o problema são mutuamente excludentes e, assim, não devem ser confundidas.

Por estas observações constata-se que a concepção corpuscular da Escola Pitagórica estava batida, sem possibilidade de saída. Os argumentos de Zenão tornaram palpável a incompatibilidade dessa concepção com a estrutura da reta. Mas essa incompatibilidade já estava revelada pela existência das incomensurabilidades isto é, o fato de existirem alguns valores que não podem ser expressos em números inteiros.

A ideia de chegar a um bom termo com a incomensurabilidade, usando um número infinito de unidades muito pequenas, como haviam feito os pitagóricos, era rejeitada por Zenão, por não se adaptar à perspectiva de Parmênides, e os paradoxos tinham por finalidade refutar a solução pitagórica. Os paradoxos questionavam algumas ideias geométricas básicas, assim como ideias numéricas, particularmente a que considera a linha reta feita de um número de pontos consecutivos. Zenão também a atacou com o paradoxo da dicotomia.

Os paradoxos de Zenão entravam também em conflito com algumas concepções antigas e intuitivas sobre o infinitamente pequeno e o infinitamente grande. Acreditou-se sempre que a soma de um número infinito de quantidades podia tornar tão grande quanto se quisesse, mesmo que cada quantidade fosse extremamente pequena como ; e também que a soma de um número finito ou infinito de quantidades de dimensão zero era zero, tais como  e . O criticismo de Zenão desafiou estas concepções e os seus paradoxos criaram uma agitação cujos efeitos ainda podem ser observados atualmente.

Em termos modernos, a sequência dicotômica, no primeiro argumento de Zenão, é a progressão geométrica [11]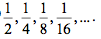. A série gerada por uma sequência geométrica é chamada de progressão geométrica. Uma sequência geométrica decrescente gera uma progressão convergente. Se a sequência começa com o termo  e razão igual a q, o limite é dado pela fórmula: 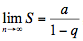, e essa expressão é chamada de limite da soma dos termos de uma progressão geométrica infinita e decrescente. Essa progressão gera a série:  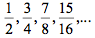que converge para , como pode ser comprovado pela fórmula do limite da soma de uma progressão geométrica. Assim, a soma: 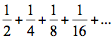, representa o número finito , apesar do argumento de Zenão, de que essa soma se estende por um número infinito de termos. A introdução dos conceitos de convergência e de limite pode encontrar objeções em um campo ou outro, mas, se aceita, fica enfraquecido o argumento de Zenão, de que a soma de uma série infinita de números deve, necessariamente, ser infinita.

O argumento referente a Aquiles e a tartaruga, também envolve uma progressão geométrica. Supondo que Aquiles avança à média de 100 metros por minuto e a tartaruga à média de 1. De acordo com Zenão, Aquiles nunca ultrapassará a tartaruga, mesmo se a vantagem inicial for de  metros. O bom senso diz que Aquiles ganha, em relação à tartaruga,  metros por minuto e que a distância original de  metros desaparecerá ao fim dos dez primeiros minutos. Mas se o argumento é feito à maneira de Zenão, no momento em que Aquiles alcançar a posição originalmente mantida pela tartaruga, esta terá avançado  1/100 de 9,9, ou seja,  0,099 metro. Mas o que foi dito uma vez sempre pode ser repetido. A vantagem diminui na progressão geométrica: 990, 9,9 , 0,099, 0,00099..., cuja soma, pela fórmula, é 1000. Aquiles terá andado  metros antes de alcançar a tartaruga, e isso lhe tomará  minutos. Mais uma vez, a soma de um número infinito de termos pode ser finita. Mas para a superação do paradoxo de Zenão, era necessário o aprimoramento da idéia de continuidade, que proporcionaria melhores elementos para justificar esses paradoxos.

Resumindo, segundo a opinião de Radice (1981, p. 44), Zenão não queria demonstrar a impossibilidade do movimento, mas reduzir ao absurdo as teses dos pitagóricos, que compunham o contínuo com átomos (pontos, mônadas) de dimensão finita. Na hipótese pitagórica, a soma de um número crescente de segmentos, ainda que decrescentes e cada vez menores, deve tender para o infinito, porque cada um conteria um número inteiro de átomos dotados de dimensões, que seria equivalente a efetuar a soma de infinitos números inteiros, que tende para o infinito. Apesar da discordância entre a experiência sensível e a aparente força dos argumentos (Giles, 1979, p. 40), o pensamento de Zenão teve um resultado positivo, pois obrigou a uma revisão crítica de conceitos fundamentais, tais como: infinito, contínuo, número, tempo e movimento.

Morris (1999, p. 25) afirma que à primeira vista, parece que o paradoxo de Zenão pode ser resolvido com bastante facilidade. Basta um pouco de aritmética. Um momento de reflexão mostrará que não é assim. Zenão não disse que Aquiles seria incapaz de alcançar a tartaruga em um tempo finito. Sabia perfeitamente que era exatamente isso que aconteceria. O que Zenão disse realmente foi que era impossível para Aquiles efetuar um número infinito de atos.

3. O Infinito com Relação ao Tempo e Espaço na Primeira Antinonia de Kant

Perseguindo a afirmação de Borges (1999, p.186) ... Admitamos lo que todos los idealistas admiten: el carácter alucinatorio del mundo. Hagamos lo que ningún idealista ha hecho: busquemos irrealidades que confirmen ese carácter. Las hallaremos, creo, en las antinomias de Kant..., o nosso objetivo neste tópico é uma melhor compreensão dos possíveis significados da primeira antinomia de Kant, em suas relações com o infinito.

As antinomias de Kant se encontram na obra Crítica da Razão Pura, publicada em 1781, e que explica essencialmente porque as metafísicas são voltadas ao fracasso e porque a razão humana é impotente para conhecer o fundo das coisas. Mas, antes de tratarmos de antinomias, julgamos importante colocar a opinião de alguns dos muitos estudiosos da obra de Kant, sobre as dificuldades e contradições dos temas tratados pelo grande filósofo.

Cretella Júnior (1967, p. 130-131) assegura que a primeira dificuldade com que esbarra o estudioso da obra de Kant é a nomenclatura ou terminologia que tem neste autor uma singularidade: os vocábulos são tomados ora no sentido etimológico [12], ora Kant lhes atribui significado diverso do corrente. Crítica não tem em Kant, o sentido de censura, reprovação ou aprovação, mas o de estudo, investigação, pesquisa. Puro não tem o sentido de "livre de impurezas", mas sim o de independente da experiência. Crítica da razão pura, título do livro, nada indica ao leitor que não conheça os sentidos das palavras que o compõe, mas, dentro da terminologia do autor, significa: Investigação da razão funcionando independentemente da experiência. Estética não é a ciência do belo, mas é tomada por Kant em sentido etimológico, significando sensação, percepção, percepção sensível. Transcendental não e algo muito importante, sendo tomado por Kant no sentido de o que existe em si e por si, independente de mim, no sentido de condição para que algo seja objeto do conhecimento. Experiência é a percepção sensível; número ou noumena, palavra empregada por Platão no Timeu, é a realidade inteligente, objeto da razão, oposta à realidade sensível, realidade absoluta, a coisa em si; fenômeno é tudo que é objeto da experiência possível, tudo que aparece no tempo e no espaço e que manifesta as relações determinadas pelas categorias. Coisa em si é o que subsiste em si mesmo, sem supor outra coisa. Analítico não possui relação com análise, divisão de um todo em partes, nem sintético se refere a resumo, a síntese.

Segundo Russell (1995, p. 324) uma proposição analítica é aquela em que o predicado forma parte do sujeito; por exemplo, "um homem alto é um homem" ou "um triângulo equilátero é um triângulo". Tais proposições se deduzem do princípio da contradição; sustentar que um homem alto não é um homem seria contraditório. Uma proposição sintética é a não analítica. Todas as proposições que conhecemos somente pela experiência são sintéticas. Não podemos por mera análise de conceitos descobrir verdades como: "A segunda feira foi um dia úmido" ou "Napoleão foi um grande general", frases somente comprovadas pela experiência. Para Kant todas as proposições sintéticas somente são conhecidas por meio da experiência.

Um dos estudiosos de Kant, Jean Lacroix (p. 115) afirma sobre outras dificuldades: Não escondemos as dificuldades internas do sistema kantiano. De todas as obras filosóficas, disse-se, a Crítica da Razão Pura é, ao mesmo tempo, a mais genial e a mais contraditória. Porque as suas contradições são as próprias contradições do real. O homem kantiano é uma dualidade, uma "duplicidade" em busca de unidade. Russell (2001, p. 342) afirma que as obras de Kant abordam enorme variedade de temas que ele ensinou em uma ou outra época e que pouco desse material ainda interessa nos dias de hoje. Na opinião de Russell (1995, p. 330-331) a parte mais importante da Crítica da Razão Pura é a doutrina do espaço e tempo, objeto da primeira antinomia que interessa diretamente ao nosso estudo. Russell ressalta que explicar com clareza a doutrina kantiana do espaço e do tempo não é objeto fácil, porque a mesma teoria não é clara. Por estas opiniões constata-se não ser uma tarefa fácil esta busca pela compreensão da afirmação de Borges sobre a antinomia de Kant relacionada com o tempo e o espaço, em que está embutida a ideia de infinito.

Na opinião de Porta (2002, p. 108) o objetivo de Kant em Crítica da Razão Pura, é justificar a física de Newton contra o empirismo [13] e o ceticismo [14]. A ciência é para Kant, a geometria euclidiana e a mecânica newtoniana. Na primeira metade do século XVII, existiam na Alemanha duas físicas a de Descartes e a de Leibniz. A física de Newton aparece como uma nova e poderosa concorrente, que as desloca. Kant inicia sua formação em física através do contato com as polêmicas entre cartesianos [15] e leibnizianos [16], para em seguida aderir a Newton.

Para Kant, o grau de ciência presente em qualquer disciplina é proporcional à quantidade de Matemática que nela existe, pois todas as proposições da Matemática são sempre juízos a priori [17], conhecimento puro, que em princípio independe da experiência, conhecimento que não provém da prática, mas que é inerente ao próprio espírito humano que se tornam possíveis pela existência das ideias natas, necessárias e anteriores à experiência a posteriori. Esse último conhecimento empírico que se reduz aos dados fornecidos pelas experiências sensíveis é tudo o que deriva da experiência. Russell afirma (2001, p. 343) que o importante é que estas duas classificações se entrecruzam. Kant encontrou um único exemplo para a comprovação de sua tese: nas proposições da Matemática. E que os postulados da geometria euclidiana são juízos a priori impostos ao espírito humano, e que sem esses postulados não é possível nenhum raciocínio consistente sobre o espaço. (EVES, 1995, p. 545), (KARLSON, 1961, p. 580).

Kant declara que a idealidade do espaço e do tempo era a chave da filosofia transcendental (significa a priori, isto é, simultaneamente anterior à experiência e condição da experiência). Que qualquer ciência comporta juízos sintéticos a priori e a matemática, sobretudo é essencialmente a priori. A verdadeira distinção é que o saber científico comporta sempre um elemento intuitivo. As intuições (se refere a um objeto) que correspondem à matemática são o espaço e o tempo formas puras a priori da sensibilidade (a sensação refere-se apenas ao sujeito, por sensibilidade entende Kant a faculdade de ter percepções) (LACROIX, p. 35-36).

Kant (Pascal, 1983, p. 51-52) considera que o espaço e o tempo dependem unicamente da forma de nossa intuição, da constituição subjetiva de nosso espírito. O espaço é a priori, e não um conceito: isto é, ele é uma intuição pura, a priori. É nessa intuição pura do espaço que se baseia a geometria. As definições e os postulados enunciam as propriedades do espaço, e tais enunciados não têm valor universal e necessário, ou seja, apodítico [18], senão porque o espaço é uma intuição a priori. Se o espaço fosse um conceito, as proposições geométricas seriam simplesmente analíticas; se fosse uma intuição empírica, seriam a posteriori. Na verdade, elas são ao mesmo tempo sintéticas e a priori, e não se pode compreendê-las sem fazer do espaço uma intuição pura (PASCAL, 1983, p. 52-53), (OMNÈS, 1995, p. 98).

Assim, o espaço não pode ser um conceito empírico, a posteriori, formado a partir a experiência exterior, visto como, ao contrário, toda experiência exterior supõe o espaço. O espaço é uma estrutura já existente no espírito humano. Ele é a priori, porque a sua representação é a própria condição da possibilidade dos fenômenos. Assim, pode-se conceber um espaço em que não houvesse objeto algum, mas não se pode perceber um objeto fora do espaço. As relações espaciais são constitutivas do objeto. O espaço não é conceitual, pois considerado do ponto de vista de sua compreensão, um conceito é constituído de elementos mais simples que ele; mas, uma parte do espaço não é mais simples que o espaço visto como um todo. Do ponto de vista da extensão, um conceito deve aplicar-se a objetos diversos; o espaço de maneira contrária, não é aplicável senão a ele mesmo: ele é uno. Todos os conceitos de espaço supõem uma intuição a priori, da qual eles são meras limitações. O espaço somente pode ser uma intuição, visto conter em si uma multidão infinita de representações, o que seria impossível se fosse um conceito, que é apenas a representação do caráter comum de uma multidão infinita de representações possíveis. O espaço é representado como uma grandeza infinita dada.

Pascal afirma que a análise com relação ao tempo, é similar a do espaço. O tempo não é um conceito empírico, a posteriori, extraído de alguma experiência; pois, somente percebemos as relações temporais de simultaneidade ou de sucessão por termos, antes, a representação do tempo. Portanto, esta não pode originar-se da experiência, visto que a experiência (interna) a supõe. É um quadro de representação necessário que precede a percepção e a intuição. O tempo é uma representação necessária que serve de fundamento a todas as intuições. Os fenômenos podem desaparecer, mas não o tempo. Tudo se passa no tempo, mas o tempo não passa, assim, ele é dado a priori. Quando se diz que os tempos diferentes não são simultâneos, mas sucessivos, este princípio tem valor apodítico, ou seja, existe a consciência de sua necessidade e universalidade. Esse princípio não pode ser extraído da experiência, pois ao contrário, é ele que fundamenta a experiência. O tempo não é um conceito discursivo ou, como se diz, um conceito geral, mas uma forma pura da intuição sensível. Não é possível conceber tempos diferentes senão como partes de um mesmo tempo, cuja representação, sendo una, terá de ser intuitiva. Como os diferentes conceitos de tempo não passam de limitações do tempo em geral, assim, a representação originária deste último é infinita, isto é, intuitiva. Concluindo, o tempo é uma intuição pura, como o espaço e, enquanto tal é a condição do todo vir-a-ser. (PASCAL, 1983, p. 54-55), (OMNÈS, 1995, p. 98)

Apresentaremos a primeira antinomia de Kant (2003, p. 356):

Tese: O mundo tem um começo no tempo e é por isso limitado no espaço, e

Prova: Vamos admitir que o mundo não tenha um começo no tempo.

Assim, até cada instante determinado, transcorreu uma eternidade e, portanto, aconteceu uma série infinita de estados sucessivos das coisas no mundo. Kant declara que a infinitude de uma série está exatamente no fato dela jamais poder ser acabada mediante uma síntese sucessiva. E desde modo, uma transcorrida série cósmica infinita é impossível e um início do mundo é, pois, uma condição necessária da sua existência. Isso é o primeiro ponto a demonstrar.

Com relação ao segundo ponto, Kant (2003, p. 356-358) afirma que se admitirmos novamente o ponto de vista contrário, que o mundo não é limitado no espaço, ele será uma totalidade infinita de coisas que existem ao mesmo tempo. Dessa forma, a grandeza de um quantum, que não é dado dentro dos limites determinados de uma intuição [19] qualquer, não se pode pensar de outro modo que não seja a síntese das partes, e a totalidade de um quantum desse gênero somente pode ser pensada pela síntese completa ou pela repetida adição da unidade a si mesma. [20] Consequentemente, para pensar como uma totalidade o mundo que preenche todos os espaços, teria de considerar-se completa a síntese sucessiva das partes de um mundo infinito, ou seja, teria de considerar-se decorrido um tempo infinito na enumeração de todas as coisas coexistentes, o que é impossível. Nesse seguimento um agregado infinito de coisas reais não pode considerar-se uma totalidade dada, nem, portanto dada simultaneamente. Assim, o mundo não é infinito quanto à extensão no espaço, mas, antes, é encerrado em limites. Esse é o segundo ponto a demonstrar.

Na Antítese (Kant, 2003, p. 357), o mundo não tem nem começo nem limites no espaço. É infinito tanto no tempo quanto no espaço. Na Prova, inicialmente o autor faz a suposição de que o mundo tenha um início: Como o começo é uma existência precedida de um tempo em que a coisa não é, teve de ter decorrido previamente um tempo em que o mundo não era, ou seja, um tempo nulo.

Kant (2003, p. 357) segue afirmando que, em um tempo nulo é impossível o aparecimento de qualquer coisa, porque nenhuma parte de um determinado tempo possui em si, preferencialmente a outra, uma condição que distinga a existência e a faça prevalecer sobre a não-existência – admitindo-se que tal condição surja por si mesma ou através de uma outra causa. Nesse sentido, podem começar no mundo diversas séries de coisas, conquanto o próprio mundo não possa ter começo e é por isso infinito com respeito ao tempo passado.

Em relação ao segundo ponto, Kant (2003, p. 357-359) admite inicialmente o contrário, isto é,

que o mundo é finito e limitado quanto ao espaço, encontra-se em um espaço vazio que não é limitado. Então, não haveria apenas uma relação das coisas no espaço, mas ainda uma relação das coisas ao espaço. Como o mundo é uma totalidade absoluta, fora da qual não há objeto algum da intuição, nem, por conseguinte, um correlato do mundo com o qual este esteja relacionado, a relação do mundo com um espaço vazio não seria uma relação a um objeto. Semelhante relação, porém não é nada e, consequentemente, também não é nada a limitação do mundo pelo espaço vazio. Logo, o mundo não é limitado quanto ao espaço, ou seja, é infinito em extensão. [21]

Na Nota à Primeira Antinomia, na Tese, Kant (2003, p. 358-361) escreve que nestes argumentos contrastantes, não procurou fantasmagorias [22] para conduzir uma prova que iluda a falta de percepção ou o deslize do opositor. Afirma que cada um dos argumentos foi tirado da natureza das coisas, opondo-se a vantagem que poderiam ser oferecidas pelas falsas inferências dos dogmáticos dos dois lados. Escreve que aparentemente poderia ter provado a tese, colocando de antemão um conceito vicioso da infinidade de uma grandeza dada, segundo o hábito dos dogmáticos. Para Kant, uma grandeza é infinita quando não é possível outra maior (segundo ele, que ultrapasse o número de vezes que uma unidade dada está nela contida). Afirma que, desta maneira, nenhum número é o maior, porque sempre podem ser-lhe acrescentadas unidades. Assim, é impossível uma grandeza infinita dada e, por conseguinte, é impossível também um mundo infinito (tanto com respeito à série transcorrida como também com relação à extensão). Dessa forma, por ambos os lados é limitado.

Kant afirmou que era absurdo supor que o tempo era infinito (MORRIS, 1998, p. 33). Granger (2002, p. 214-215) destaca que a Tese de Kant é demonstrada pelo fato de que uma série infinita decorrida de momentos do mundo, sendo por definição inacabada, é impossível. Se uma quantidade infinita de tempo tivesse transcorrido antes do presente, teria de haver ocorrido um número infinito de eventos, o que era impossível. Kant não estava tentando provar que o tempo é finito. Na verdade, ele apresentou outro argumento que parecia levar à conclusão oposta; acreditava poder mostrar que a ideia de tempo finito também leva a uma contradição. O tempo não pode ter um começo porque nesse caso se poderia perguntar o que aconteceu antes desse ponto. Não podia ter um fim porque nesse caso se poderia perguntar o que aconteceu depois. Kant estava tentando provar que, como não podia ser infinito nem finito, o tempo não era uma propriedade do mundo externo. Ao contrário, tinha de ser algo inato na mente humana, não uma característica do mundo externo.

Granger (2002, p. 214-215) destaca que a Antítese é demonstrada pelo fato de que um começo do mundo suporia um tempo anterior vazio (nulo), no qual é impossível o surgimento de qualquer coisa (KANT, 2003, p. 357). Granger não faz comentários sobre a natureza dessa dupla argumentação e também não destaca a sua heterogeneidade. Diz que a solução proposta consiste em denunciar uma confusão da realidade empírica do mundo como fenômeno e de sua realidade suposta como coisa em si. Se o mundo não é dado como coisa em si, ele não existe nem como todo finito nem como todo infinito, e a antinomia somente aparece como:

... o conflito de uma aparência proveniente de se ter aplicado a ideia da totalidade absoluta, válida unicamente como condição da coisa em si, a fenômenos, que só existem na representação, e quando constituem uma série, na regressão sucessiva, mas que não existem de qualquer outro modo.

(Kant, 2003, p. 403)

Na opinião de Granger (2002, p. 215), solução de difícil aceitação para uma ciência moderna que recusaria de forma geral o aspecto idealista, ou subjetivo, do transcendental, isto é, da pura razão.

Morris (1998, p. 33-34) declara que a questão do caráter finito ou infinito do tempo vem sendo debatida desde a Antiguidade; e que mesmo atualmente, os cientistas não sabem realmente se o tempo é infinito ou finito.

A concepção de espaço de Kant de seus discípulos (Omnès, 1995, p. 99), exclui qualquer perspectiva de um espaço irrepresentável, por exemplo, não euclidiano. Um espaço-tempo como o de Albert Einstein (1879-1955), cujas propriedades de curvatura são determinadas pela matéria que ela contém, ou seja, pelos "objetos", se contrapõe ainda mais a todos os postulados de Kant.

Omnès (1995, p. 99) afirma que apesar da preocupação de Kant em superar seus predecessores, não deixa de estabelecer outros limites, que se revelam igualmente frágeis, como se pode constatar na leitura de suas "antinomias" e, em particular, da primeira, nosso objeto de atenção. Ela contrapõe duas teses: uma afirma que o tempo é eterno e o espaço, infinito; a outra, que há um começo no tempo e que o espaço é limitado. Kant pretende estabelecer por métodos "transcendentais", isto é, pela razão pura, que é fundamentalmente impossível decidir entre essas duas afirmações. Entretanto a cosmologia moderna pensa ter sólidos argumentos a favor da existência de um começo no tempo e que considera o caráter finito ou infinito do espaço como uma questão que pode ser resolvida, em princípio, medindo com bastante exatidão a densidade atual de massa no espaço.

Ao se falar de tempo e espaço é impossível não recorrer a Física. E acrescentando a dificuldade apresentada anteriormente por Russell e outros estudiosos, na questão da falta de clareza na teoria de Kant, Kneller (1980, p. 48) destaca outra dificuldade. A Física contemporânea apresenta duas teorias orientadoras, a relatividade geral e a mecânica quântica, teorias mutuamente incompatíveis. Segundo a relatividade geral, a matéria é um aspecto do espaço-tempo, que é contínuo e determinista [23]. Com relação à mecânica quântica, a matéria é descontínua ou particulada (mas com características ondulatórias) e fundamentalmente não determinista. A relatividade geral, além disso, foi alvo de uma sucessão de críticas durante mais de meio século. A situação da mecânica quântica ainda está pior, porquanto emprega os conceitos contraditórios de onda e partícula. Constata-se que a teoria em uso experimental é uma conjunção de duas teorias parcialmente incompatíveis. Portanto, enquanto não se propor uma teoria que unifique a mecânica quântica e a reconcilie com a relatividade geral, não se pode afirmar que os cientistas descobriram as leis fundamentais da matéria.  Quando os problemas com que as teorias atuais se defrontam forem resolvidos, outros certamente persistirão. Esta afirmação confirma uma vez mais a dificuldade de entendimento do tema estudado neste artigo.

Kneller (1980, p. 49) segue com várias indagações: Será que a própria natureza excede a nossa capacidade de compreensão? O universo pode muito bem consistir em uma infinita variedade de coisas dispostas em uma sucessão infindável de níveis ou domínios relativamente independentes. Esses níveis incluem o nível humano, o nível de animais e plantas, o nível de objetos inanimados (rios, pedras etc.), o nível das moléculas e átomos, e o nível das partículas elementares. Acima e abaixo desses níveis, devemos esperar o descobrimento de outros. Haverá coisas demais para descobrirmos? Kneller afirma que a pergunta parece irrespondível, pois como poderemos chegar ao conhecimento se já explicamos totalmente a ordem natural? Tudo o que poderemos dizer é que os nossos esforços sumamente persistentes não conseguiram levar-nos mais longe.

Existem alguns limites a priori para o que podemos saber? A Ciência é limitada pela amplitude da mente e dos sentidos humanos. Existem noções que não podemos formular de um modo significativo para investigação, porque, como disse Kant, as nossas categorias mentais não permitem. Como exemplo Kneller (1980, p. 49) afirma que não podemos propor uma teoria científica que negue a existência de espaço e tempo, porquanto é impossível pensarmos no mundo físico sem esses conceitos. Por um lado, se o universo é infinito, existem partes que nunca observaremos. Se for finito, por outro lado, observaremos a maioria de suas partes somente como elas costumavam ser.

4. Borges e o Paradoxo de Aquiles e a Tartaruga

Gutièrrez afirma que Borges entendeu o infinito e compartilhou seus mistérios insondáveis, mesmo naqueles aspectos aparentemente áridos e distantes, como a álgebra. E que provavelmente, nunca saberemos quem seduziu a quem, e é evidente que em pouco tempo, ambos alcançaram um grau de compreensão mútua. Diz também que a paixão de Borges pelo infinito se arrastava desde a infância do grande escritor, com as explicações de seu pai sobre os paradoxos de Zenão, sobre um tabuleiro de xadrez. Outro elemento que pode ter colaborado nessa paixão de Borges pelo infinito pode ser sido as compridas e calorosas tardes rioplatenses, de sua adolescência. Com relação à afirmação anterior de Gutièrrez, indagamos. Será realmente que Borges ou algum outro estudioso entendeu o infinito?

Um dos grandes sonhos de Borges era escrever uma biografia do infinito:

Eu sonhei compilar alguma vez sua móvel história (do infinito). A numerosa Hidra (monstro palustre que vem a ser uma prefiguração ou um emblema das progressões geométricas) daria conveniente horror a seu pórtico; a coroariam os sórdidos pesadelos de Kafka e seus capítulos centrais não desconheceriam as conjecturas do remoto cardeal alemão – Nicolás de Krebs, Nicholas Cusa [24]– que na circunferência viu um polígono de número infinito de ângulos e deixou escrito que uma linha infinita seria uma reta, seria um triângulo, seria um círculo e seria uma esfera. Cinco, sete anos de aprendizagem metafísico, teológico, matemático, me capacitariam (talvez) para planejar decorosamente esse livro. Inútil afirmar que a vida me proíbe essa esperança, e ainda esse advérbio.
(Borges, 1999, p. 175-176, tradução livre)

Assim, Borges afirma sobre a grande dificuldade e os desafios sobre as tentativas da construção da história do infinito. No ensaio, Avatares da Tartaruga, declara que seu propósito é registrar certas transformações do paradoxo de Zenão, Aquiles e a Tartaruga; e recorda esse paradoxo:

Aquiles corre dez vezes mais rápido que a tartaruga e lhe dá uma vantagem de dez metros.  Aquiles corre esses dez metros, a tartaruga corre um; Aquiles corre esse metro, a tartaruga corre um decímetro; Aquiles corre esse decímetro, a tartaruga corre um centímetro; Aquiles corre esse centímetro, a tartaruga um milímetro; Aquiles corre o milímetro, a tartaruga um décimo de milímetro e assim infinitamente, sem alcançá-la.
(Borges, 1999, p. 176, tradução livre)

Borges apresenta em seguida, um texto de Aristóteles [25] , que afirma que o mais lento não será alcançado pelo mais rápido, pois é necessário que o perseguidor passe pelo local que o perseguido acaba de passar, de tal maneira que o mais lento sempre está com uma determinada vantagem. Afirma também que esse argumento ficou conhecido e teve a sua difusão, junto com a série: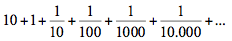

Argumenta Zenão que o movimento é impossível, pois o móvel deve atravessar o ponto médio para chegar ao fim e antes o ponto médio do ponto médio, e assim sucessivamente, como tínhamos afirmado anteriormente.

Borges afirma (1999, p. 177) que foi Aristóteles quem fez a primeira refutação desses argumentos, e a recordação desses argumentos, lhe inspira o argumento do terceiro homem frente a doutrina platônica. Essa doutrina quer demonstrar que dois indivíduos que possuem atributos comuns (por exemplo dois homens) são apenas aparências temporais de um arquétipo.

Apesar de constar que já foram dadas várias opiniões muito qualificadas sobre os paradoxos de Zenão, e que a sua opinião poderia parecer trivial, Borges afirma (1999, p. 162) que Zenão é incontestável, salvo que confessemos a idealidade do espaço e do tempo. Aceitemos o idealismo, aceitemos o crescimento concreto do percebido, e nos esquivaremos das bordas dos abismos do paradoxo.

5. Conclusão

Mesmo antes deste aprofundamento que fizemos com relação ao infinito, baseado nas afirmações de Borges em um de seus ensaios, já observávamos o quanto esse assunto povoa a imaginação de pessoas ligadas ou não aos meios científicos.

Constatamos que o tema infinito aparece em muitos momentos no decorrer da história da humanidade. Percorremos tópicos das contradições nas antinomias de Kant, o aspecto desencadeador de argumentos dos paradoxos de Zenão, e a visão literária de Borges com relação ao infinito, embasada em grande parte nas considerações de Zenão e Kant.

Observamos em Zenão, Kant e Borges argumentos que nos mostram o quanto ainda existe de mistério e interesse nesse conceito que desafia estudiosos de várias áreas do conhecimento. Não apresentamos respostas finais sobre o assunto; pois sabemos que as mesmas não existem, apesar de todo o progresso filosófico/científico da humanidade. Apenas discorremos sobre algumas questões observadas nos paradoxos de Zenão e nas antinomias de Kant, que Borges genialmente procurou relacionar.

6. Bibliografia

ABBAGNANO, Nicola, Dicionário de Filosofia, São Paulo: Martins Fontes, 1999.

ARISTOTLE, Physics, Oxford: Oxford University Press, 1999.

BARNES, Jonathan, Filósofos Pré-Socráticos, São Paulo: Martins Fontes, 1997.

BORGES, Jorge Luis. Discusión, Buenos Aires: EMECÉ Editores S.A., 1999.

CARAÇA, Bento de Jesus, Conceitos Fundamentais de Matemática, Lisboa: Gradiva, 1997.

COBIANCHI, Antonio Sérgio, Estudos de Continuidade e Números Reais: Matemática, Descobertas e Justificativas de Professores. 2001. 433 p. Tese de Doutorado em Educação Matemática, Departamento de Matemática, UNESP – Rio Claro.

COLLETTE, Jean-Paul, Historia de las Matemáticas I, México: Siglo Veintiuno Editores, 2000.

COSTA, Manoel Amoroso, As Idéias Fundamentais da Matemática e Outros Ensaios, 3 edição, São Paulo: Editora Convívio e EDUSP – Editora da Universidade de São Paulo, 1981.

CRETELLA JÚNIOR, José, Novíssima História da Filosofia. São Paulo: José Bushatsky, 1967.

FERREIRA, Aurélio Buarque de Holanda, Novo Dicionário da Língua Portuguesa, Rio de Janeiro, 1986.

EVES, Howard, Introdução à História da Matemática. Campinas: Unicamp, 1995.

GILES, Thomas Ransom, Introdução à Filosofia, São Paulo: EPU: Editora da Universidade de São Paulo, 1979.

GRANGER, Gilles Gaston, O Irracional, São Paulo:Editora Unesp, 2002.

GUILLEN, Michael, Pontes para o Infinito, Lisboa: Gradiva, 1987.

GUTIÉRREZ, Claudio, Borges y el Infinito: Testimonios de un amor correspondido, texto não publicado.

KARLSON, Paul, A Magia dos Números, Porto Alegre: Globo, 1961.

KANT, Immanuel, Crítica da Razão Pura, São Paulo: Martin Claret, 2003.

KLINE, Morris, Mathematical Thought from Ancient to Modern Times, New York: OxfordUniversity Press, 1972.

KNELLER, G.F., A Ciência como Atividade Humana, Rio de Janeiro: Zahar/Edusp, 1980.

LALANDE, André, Vocabulário Técnico e Crítico da Filosofia, São Paulo: Martins Fontes, 1999.

LACROIX, Jean, Kant e o Kantismo, Porto: Rés-Editora Lda.,

MONDIN, Battista, Curso de Filosofia, v.1, São Paulo: Edições Paulinas, 1981.

MORRIS, Richard, Uma Breve História do Infinito – Dos Paradoxos de Zenão ao Universo Quântico, Rio de Janeiro: Jorge Zahar Editor, 1998.

OMNÈS, Roland, Filosofia da Ciência Contemporânea, São Paulo: Unesp, 1996.

PASCAL, Georges, O Pensamento de Kant, Petrópolis: Vozes, 1983.

PORTA, Mario Ariel Gonzáles, A Filosofia a partir de seus problemas, São Paulo: Edições Loyola, 2002.

RADICE, Lucio Lombardo, O Infinito: De Pitagóras a Cantor itinerários filosóficos e matemáticos de um conceito de base, Lisboa: Editorial Notícias-Biblioteca de Conhecimentos Básicos, 1981.

RUSSELL, Bertrand, História de la Filosofia Occidental, Madrid: Editorial Espasa Calpe, S.A., 1995.

RUSSELL, Bertrand, História do Pensamento Ocidental: A Aventura das Idéias dos Pré-Socráticos a Wittgenstein, Rio de Janeiro: Ediouro Publicações, 2001.

STEPHEN, F. Barker, Filosofia da Matemática, Rio de Janeiro: Zahar Editores, 1969.

1. Professor do Programa de Pós Graduação em Projetos Educacionais de Ciências, Escola de Engenharia de Lorena, Universidade de São Paulo – EEL – USP.: Email: cobee@debas.eel.ups.br

2. Estoicismo: Uma das grandes escolas filosóficas do período helenista fundada por volta de 300 a.C., por Zenão de Cicio. Estóica, porque Zenão o fundador da Escola, ensinava sob os pórticos (stoá) de Atenas. Os principais mestres dessa escola foram, além de Zenão, Cleante de Axo e Crisipo de Soles. Como as escolas da mesma época, o epicurismo e o ceticismo, o estoicismo compartilhou a afirmação do primado da questão moral sobre as teorias e o conceito de filosofia como vida contemplativa acima das ocupações, das preocupações e das emoções da vida comum. (Abbagnano, 1999, p. 375). (grifos nossos). Segundo Mondin (1981, p. 110) o estoicismo é uma doutrina essencialmente moral. Mas contém algumas doutrinas importantes sobre o conhecimento humano e sobre a estrutura do cosmo. Para eles, a estrutura do cosmo resulta de dois elementos, a matéria e o Logos (razão). A primeira, indefinida e inerte, representa o princípio passivo; o segundo, animado e cheio de energia, representa o princípio ativo. Esta concepção dualista do cosmo não tem grande originalidade. A novidade está nos argumentos aduzidos pelos estóicos, como prova da existência do Logos, e também no modo de concebê-lo. Como o homem é dotado de razão, eles admitiram o Logos como elemento primordial do cosmo. Como o homem é manifestação do Logos e como o todo não pode ser menos perfeito do que as suas partes, não se pode aceitar que o cosmo seja destituído de razão. O Logos não é de natureza espiritual, mas material, porque segundo os estóicos, o que não tem corpo não pode agir. Ele é constituído de uma matéria especial, sutilíssima, agilíssima, que pode penetrar em qualquer coisa. Alguns deles identificaram a matéria sutilíssima da que é feita o Logos com o fogo, outros com o éter.

3. J. W. Richard Dedekind (1831-1916): Nasceu em Braunschweig, sendo um dos quatro filhos de uma família luterana. Com a idade de 22 anos se doutorou em Göttingen, com uma tese sobre o Cálculo, que foi elogiada por Carl Friedrich Gauss (1777-1855). Permaneceu em Göttingen durante alguns anos, ensinando e assistindo às aulas de Peter Gustav Leujeune Dirichlet (1805-1859). Depois se dedicou ao ensino secundário, principalmente em Brunswick, na Tecnische Hochschule, pelo resto de sua vida

4. Aristóteles (384-322 a.C.): Foi discípulo de Platão em uma época em que a figura principal da Academia platônica era Eudoxo de Cnido. Ao matematismo que dominava a Academia, ele contrapôs o espírito de observação e a índole classificatória, típicas da investigação científica naturalista, e que constituíram traços fundamentais de seu pensamento. Foi mestre de Alexandre, o Grande. Era um filósofo e biólogo, mas estava completamente a par das atividades dos que estudavam matemática. Dedicou muita atenção aos paradoxos de Zenão, mas procurou refutá-los baseado no senso comum. Por ter hesitado em acompanhar os matemáticos platônicos nas abstrações e tecnicalidades da época, não deu contribuição importante ao assunto. Além disso, por ter fundado a lógica e por suas frequentes alusões a conceitos e teoremas matemáticos em sua obra pode-se considerar que Aristóteles contribuiu para o desenvolvimento da Matemática. A discussão aristotélica sobre o infinito potencial e atual da aritmética e geometria influenciou muitos dos que mais tarde escreveram sobre fundamentos da Matemática. De significado mais positivo é a análise que Aristóteles fez do papel das definições e hipóteses na Matemática

5. Nasceu em Buenos Aires, Argentina, em 24 de agosto de 1899. Em 1914 viajou com sua família para a Europa e se instalou em Genebra. Foi para a Espanha em 1919 e lá entrou em contato com o movimento ultraísta. Regressando para Buenos Aires, publicou seu primeiro livro de poemas, Fervor de Buenos Aires, em 1923. Artigos em jornais e revistas, críticas literárias, livros de poemas, de ensaios e de contos, completam a sua produção e o seu nome se difunde no ambiente literário. Ingressa na Academia Argentina de Letras em 1955 e é nomeado diretor da Biblioteca Nacional, cargo que ocupou até 1973. Foi professor de literatura inglesa na Universidade de Buenos Aires. Dentro de sua vasta produção narrativa cabe citar História Universal da Infâmia, Ficções, O Aleph, O Informe de Brodie e O Livro de Areia; os ensaios como Evaristo Carriego, História da Eternidade, Discussão e Outras Inquisições, e doze livros de poemas. Sua obra foi traduzida para mais de vinte e cinco idiomas. Faleceu em Genebra em 14 de junho de 1986.

6. Entende-se atualmente por idealismo a tendência filosófica que consiste em reduzir toda existência ao pensamento, no sentido mais amplo da palavra pensamento. Opõe-se ao realismo, que afirma que a existência dos objetos independentemente do pensamento. No idealismo absoluto, o ser é reduzido à consciência. Kant chama de idealismo empírico à doutrina que declara a existência dos objetos no espaço, fora de nós, quer duvidosa e indemonstrável, quer falsa e impossível. (Lalande, 1999, p. 487-488)

7. Zenão de Eléia (cerca de 504/1 - ? a.C.): Sua produção aconteceu cerca de 464/461 a.C. Nasceu em Eleia (Itália), e interveio na política, dando leis à sua pátria. Tendo conspirado contra a tirania e o tirano (Nearco ?), acabou preso, torturado e, por não revelar o nome dos comparsas, perdeu a vida. Escreveu várias obras em prosa: Discussões, Contra os Físicos sobre a Natureza, Explicação Crítica de Empédades. É considerado o criador da dialética (entendida como argumentação combativa ou erística). Zenão erigiu-se em defensor de seu mestre, Parmênides, contra as críticas dos adversários, principalmente os pitagóricos. Defendeu o ser uno, contínuo e indivisível de Parmênides contra o ser múltiplo, descontínuo e divisível dos pitagóricos

8. Antinomia: Contradição entre duas leis ou princípios. Filos.: Conflito entre duas afirmações demonstradas ou refutadas aparentemente com igual rigor. (Ferreira, 1986, p. 132

9. Immanuel Kant (1724-1804): Nasceu em Königsberg na Prússia Oriental e nunca se afastou da mesma. Estudou na Universidade de Königsberg, onde se tornou professor catedrático. Afirma Giles (1979, p. 69) que a sua confiança na razão, reforçada pela ciência newtoniana, era inquebrantável e procurou uma fundamentação sólida para o exercício da razão. Seu pensamento é considerado o ponto de convergência do pensamento filosófico anterior.  Sua obra constitui fonte da qual brotou a maior parte das reflexões dos séculos XIX e XX. (grifos nossos

10. Parmênides: Nasceu em Eleia, hoje Vélia, na Itália. Foi um filósofo conservador, para quem a razão somente reconhece o ser absoluto, sendo toda mudança apenas aparente. Foi discípulo de Xenófanes, mas não seguiu os passos do mestre. Manteve vínculos (segundo testemunho de Sócion) com pitagórico Amínias, que o levou à placidez. O relato envolvendo Amínias levou alguns estudiosos a procurar (em vão) elementos pitagóricos no pensamento de Parmênides. Em Atenas, com Zenão, combateu a filosofia dos jônicos. Sua obra se inicia por volta de 500 a.C. Tentou ver a "realidade" última para além dos fenômenos naturais, a essência do que existe além daquilo que observamos. Ele afirma que a essência de tudo é o "Ser"; o Ser enche todo o espaço, e, então, o universo deve ser uno e ilimitado. É claro que se pode pensar no não-Ser, isto é, em um espaço totalmente vazio, em um vácuo, mas isso não é a realidade (leva a contradições lógicas intransponíveis. Tentando demonstrar que o único objeto possível de aplicação do pensamento é o Ser, Zenão criou famosos paradoxos). A atitude polêmica de Parmênides levantou-se tanto contra o dualismo pitagórico (ser e não-ser, cheio e vazio ...) como, segundo alguns intérpretes, contra o mobilismo de Heráclito. . (BARNES, 1997, p. 149)

11. O tipo mais simples de sequência e ao mesmo tempo de grande importância histórica e teórica é a sequência geométrica. Nessa, após escolher um número qualquer para o primeiro termo, e qualquer outro número para razão, passamos de um termo a outro multiplicando pela razão. Qualquer sequência repetida pode ser encarada como um sequência geométrica especial, sendo  a razão multiplicadora. Eliminando-se esse caso trivial, pode-se classificar a sequência geométrica em crescente e decrescente, respectivamente, como nos exemplos seguintes,  e

12. Etimologia: Origem de uma palavra; parte da Gramática que trata da origem das palavras.

13. Empirismo: é o nome genérico de todas as doutrinas filosóficas que negam a existência de axiomas enquanto princípios de conhecimento logicamente distintos da experiência. Do ponto de vista gnosiológico, o empirismo é a doutrina que, reconhecendo ou não a existência de princípios inatos no indivíduo, não admite que o espírito tenha leis próprias que difiram das coisas conhecidas e, por conseguinte, baseia o conhecimento verdadeiro apenas sobre a experiência, fora da qual admite apenas definições ou hipóteses arbitrárias. (Lalande, 1999, p. 300). (grifos nossos)

14. Ceticismo: no sentido mais amplo, doutrina segundo a qual o espírito humano não pode atingir com certeza nenhuma verdade de ordem geral e especulativa, nem mesmo a certeza de que uma proposição deste gênero seja mais provável que outra qualquer. Doutrina que nega a possibilidade de atingir uma verdade segura em algum domínio determinado. (Lalande, 1999, p. 149-150).

15. Cartesianismo: conjunto dos fundamentos tradicionalmente considerados como típicos da doutrina de Descartes e aos quais se faz habitualmente referência tanto no sentido de aceitar quanto de refutar. Podem ser resumidos como: a) caráter originário do cogito (penso, logo existo) como auto-evidência do sujeito pensante e princípio de todas as outras evidências; b) presença de ideias no pensamento, como únicos objetos passíveis de conhecimento imediato; c) caráter universal e absoluto da razão que, partindo do cogito e valendo-se das ideias, pode chegar a descobrir todas as verdades possíveis; d) função subordinada, em relação, da experiência (isto é, da observação e do experimento), que somente é útil para decidir nos casos em que a razão apresenta alternativas equivalentes; e) dualismo de substância pensante e substância extensa, pelo qual cada uma delas se comporta segundo lei própria: a liberdade é a lei da substância espiritual; o mecanismo é a lei da substância extensa. (Abbagnano, 1999, p. 118)

16. Para Leibniz, todos os pensamentos humanos podem ser reduzidos a poucas noções primitivas; se tais noções forem expressas com caracteres, isto é, com símbolos, é possível formar os símbolos das noções derivadas e, assim, passar a deduzir tudo o que está implícito nas noções primitivas e nas definições. Assim, será possível proceder com certeza matemática tanto à aquisição de novos conhecimentos quanto ao controle dos já possuídos e também será possível determinar antecipadamente que experiências ou novas noções são necessárias a ulteriores desenvolvimentos do conhecimento. Kant comparava a característica universal de Leibniz ao tesouro escondido de que fala uma fábula de Fedro: os filhos, a quem o pai confiara a existência do tesouro no leito de morte, remexem a terra e fertilizam-na, sendo esse o único tesouro que encontram. Característica universal de Leibniz: é a arte de formar e de ordenar os caracteres de modo que se refiram aos pensamentos, isto é, de modo que tenham entre si a mesma relação que existe entre os próprios pensamentos. Os caracteres são sinais escritos, desenhados ou esculpidos. (Abbagnano, 1999, p. 115).

17. Segundo Stephen (1969, p. 13-14), tradicionalmente pensadores racionalistas são aqueles que sustentam a primazia do conhecimento a priori. Empiristas são aqueles que atribuem maior importância ao conhecimento empírico. Uma das questões que se considera fundamental em Filosofia da Matemática é saber se o conhecimento matemático (admitindo que exista) é empírico ou a priori. Embora a distinção entre as duas espécies de conhecimento nem sempre foi claramente colocada. O termo "empírico" significa "baseado na experiência", e a expressão a priori significa "passível de obter antes da experiência". Filósofos antigos admitiam que os conceitos empíricos, ou a posteriori, correspondiam a ideias "abstraídas" pela mente a partir do que é "dado" na experiência sensorial e que os conceitos a priori correspondiam a ideias fixadas na mente por outra via. Mas, com essa distinção não fica afastada a possibilidade de existirem conhecimentos empíricos que não sejam exclusivamente traduzíveis em termos de conceitos empíricos e não fica afastada a possibilidade de existirem conhecimentos a priori que não sejam exclusivamente traduzíveis em termos de conceitos a priori. Em resumo, conhecimento empírico, ou a posteriori, é o conhecimento que requer justificação da experiência; e conhecimento a priori é o conhecimento que não necessita de justificação pela experiência. (grifos nossos)

18. Apodítico: 1. Diz-se do que é demonstrável ou do que é evidente, valendo, pois, de modo necessário. 2. Irrefutável, evidente. (Ferreira, 1986, p. 144)

19. Podemos intuir um quantum indeterminado, como uma totalidade, quando estiver encerrado dentro de limites, sem termos necessidade de construir sua totalidade pela medida, quer dizer, pela síntese sucessiva das suas partes. Certamente, os limites determinam já a integridade, posto que excluem toda a grandeza.

20. Nesse caso, o conceito da totalidade não é outra coisa que não seja representação da síntese total das suas partes, porque, como não podemos extrair o conceito de intuição da totalidade – que neste caso é impossível -, somente podemos compreendê-la, em pensamento, pela síntese das partes levadas até ao infinito.

21. Simplesmente, o espaço é a forma da intuição externa – intuição formal – mas nenhum objeto real que possa ser intuído externamente. Anterior a todas as coisas que o determinam – preenchem ou limitam -, ou antes, que dão uma intuição empírica, o espaço, segundo a sua forma, não é, com o nome de espaço absoluto, outra coisa senão a mera possibilidade de fenômenos externos, na medida em que estes podem existir em si ou acrescentar-se a fenômenos dados. Portanto, a intuição empírica não é composta de fenômenos e do espaço – da percepção e da intuição vazia. Um não é o correlato da síntese do outro, mas estão apenas unidos numa mesma intuição empírica, como matéria e forma dessa intuição. Se quisermos colocar um destes dois elementos fora do outro - o espaço fora de todos os fenômenos -, resulta daí toda espécie de determinações vazias da intuição externa, que não são, contudo, percepções possíveis. Por exemplo, o movimento ou o repouso do mundo, num espaço vazio infinito é uma determinação de ambas as coisas entre si, que nunca pode ser percebida e, consequentemente, é também o predicado de um simples ser de razão.

22. Arte de fazer aparecer, de fazer ver, figuras luminosas na escuridão. 2. Fantasma. 3. Falsa aparência: "seguiam-na devagar as ovelhas brancas,... na esperança de, com a ternura dos seus balidos, arrancarem esse pobre espírito às fantasmagorias do encantamento." (Ferreira, 1986, p. 757)

23. Determinismo: Doutrina filosófica segundo a qual todos os acontecimentos do universo, e em particular as ações humanas, estão ligados de tal forma que, sendo as coisas o que são em um momento qualquer do tempo, apenas existe para cada um dos momentos anteriores ou ulteriores um estado e um só que é compatível com o primeiro. (Lalande, 1999, p. 245)

24. Nicholas Cusa (1401-1463): Seu nome deriva do de sua cidade natal (Eves, 1995. p. 316) Cuers, junto ao rio Mosela. Filho de um pescador pobre ascendeu rapidamente à hierarquia da Igreja, chegando a cardeal. Em 1448 tornou-se governador de Roma. Apenas incidentalmente se tornou um estudioso de matemática, mas isso não impediu seu êxito com uns poucos opúsculos que escreveu sobre o assunto, sendo mais lembrado hoje principalmente por seu trabalho na reforma do calendário e por suas tentativas de quadrar o círculo e trisseccionar o ângulo. Suas contribuições matemáticas são poucas (Collette, 2000, p. 255) se reduzem ao estudo da área do círculo e na busca de uma aproximação do número por meio de construções poligonais, processo que o levou a situações envolvendo o infinito.

25. O segundo paradoxo é chamado de Aquiles. Esse postula que o mais lento não será alcançado pelo mais veloz, pois o perseguidor tem que passar pelo espaço que o perseguido acabar de deixar, de tal maneira que o mais lento sempre leva uma determinada vantagem. (Aristotle, 1999, p. 161, tradução livre)