Espacios. Vol. 36 (Nº 02) Año 2015. Pág. 13

Mapas conceituais como estratégia facilitadora para o Ensino de estatística básica

Concept maps as facilitator strategy for teaching basic statistics

Eliana Cláudia Mayumi ISHIKAWA 1; Guataçara dos SANTOS JUNIOR 2; Danieli WALICHINSKI 3; Nilcéia Aparecida Maciel PINHEIRO 4; Siumara Aparecida de LIMA 5

Recibido: 12/09/14 • Aprobado: 12/11/14

Contenido

1. Introdução

2. Educação estatística

3. Aprendizagem significativa

4. Proposta de utilização de mapas conceituais no Ensino de estatística básica

5. Considerações finais

6. Referências

1. Introdução

A compreensão de que Estatística não é apenas Matemática possibilitou o surgimento da área de pesquisa denominada Educação Estatística (CAMPOS et al., 2011). Atualmente, não há dúvidas acerca da relevância do conhecimento estatístico para a formação plena do cidadão, sendo que os conteúdos estatísticos foram incluídos nas propostas curriculares da maioria dos países. Em tais propostas define-se que a implementação da Estatística deva ocorrer desde os anos mais elementares.

É consenso entre os pesquisadores da área de Educação Estatística que o trabalho com os conteúdos estatísticos deve estar baseado em situações significativas aos alunos, de modo a permitir que os mesmos compreendam conceitos e informações mais complexas e relacionáveis entre si, podendo formar seu ponto de vista. Ou seja, é necessário formar cidadãos letrados estatisticamente. Para isso, é fundamental que o processo de ensino seja direcionado no sentido de levar o aluno a elaborar um conhecimento mais rico, mais elaborado e mais estável sobre o assunto, de forma que ocorra uma aprendizagem verdadeiramente significativa.

Neste ensaio teórico, apresenta-se uma proposta inicial para o uso de mapas conceituais como estratégia facilitadora de uma aprendizagem significativa para o ensino de conceitos estatísticos. Inicialmente foi apresentada uma breve revisão sobre os objetivos da Educação Estatística, aprendizagem significativa e mapas conceituais. Em seguida, elaborou-se um modelo de utilização de mapas conceituais envolvendo conteúdos referentes a variáveis estatísticas, representação de dados e as medidas de tendência central.

2. Educação estatística

A Estatística é uma ciência que tem por finalidade desenvolver métodos para coletar, organizar e analisar dados. A Educação Estatística, por sua vez, é uma área de pesquisa que tem por objetivo estudar e compreender como se ensina e como se aprende Estatística, levando-se em consideração "[...] aspectos cognitivos e afetivos do ensino-aprendizagem, além da epistemologia dos conceitos estatísticos e o desenvolvimento de métodos e materiais de ensino etc.," (CAZORLA, KATAOKA, SILVA, 2010, p. 22-23) visando ao desenvolvimento do letramento estatístico.

Segundo Gal (2002), pode-se considerar que um adulto é letrado estatisticamente quando o mesmo é capaz de interpretar e avaliar informações estatísticas de modo crítico, além de argumentar as conclusões a que chega a respeito de tais informações. Concepção semelhante é defendida pela pesquisadora Lopes (2010, p. 8):

"[...] Ser estatisticamente competente significa que se desenvolveram atitudes, capacidades e conhecimentos estatísticos que permitem ser crítico e reflexivo em relação à informação veiculada através de eventuais conteúdos estatísticos, mesmo em uma utilização indevida ou abusiva [...]"

Concorda-se com Campos et al. (2011) ao afirmarem que o letramento estatístico inclui capacidades básicas e importantes, necessárias para o entendimento de informações estatísticas. Segundo esses autores, tais capacidades se referem à organização de dados, construção e apresentação de diferentes modos de representação de dados, entendimento de conceitos, de símbolos e de vocabulário e, ainda, a capacidade de elaborar questionamentos acerca de informações estatísticas recebidas.

Em Campos, Wodewotzki e Jacobini (2011, p. 44) pode-se observar uma síntese acerca da competência de letramento estatístico:

Diz respeito à habilidade de comunicação estatística, que envolve ler, escrever, demonstrar e trocar informações, interpretar gráficos e tabelas e entender as informações estatísticas dadas nos jornais e outras mídias, sendo capaz de pensar criticamente sobre elas.

Assim como Walichinski (2012a), considera-se que o letramento estatístico requer a capacidade de ler e interpretar informações estatísticas, refletir qual é a intenção das mesmas, além de formar um ponto de vista em relação a uma determinada informação estatística. Portanto, para se dizer que um indivíduo é letrado estatisticamente, espera-se que o mesmo possua conhecimentos à respeito da Estatística Descritiva e da Estatística Inferencial, além de apresentar uma postura crítica diante de determinadas situações.

3. Aprendizagem significativa

A Aprendizagem Significativa idealizada por David Ausubel, tem como finalidade explicar o processo de aquisição de novos conceitos, tendo como premissa os princípios organizacionais da cognição (Gomes, et.al, 2008). Neste processo de aprendizagem, o indivíduo associa o conhecimento prévio ao novo conhecimento de maneira não-arbitrária e não-literal. Assim, o conhecimento adquirido e os conhecimentos prévios - os chamados subsunçores -  tendem a se unir de maneira hierarquizada representando abstrações de experiências do indivíduo.

Segundo Moreira (2006), o termo "subsunçor", diz respeito a um conceito, uma preposição ou uma idéia que já existe na estrutura cognitiva do indivíduo. Trata-se de um conhecimento específico, existente na estrutura de conhecimentos e que permite dar significado a um novo conhecimento que lhe é apresentado ou descoberto por ele. Neste sentido, entende-se que o conhecimento prévio é o fator preponderante no processo de aprendizagem, que a aprendizagem tem um maior significado quando parte do que já é conhecido pelo indivíduo, ou seja, dos conceitos existentes em sua estrutura cognitiva.

É importante ressaltar que na aprendizagem significativa, o aluno não pode ser considerado como um receptor passivo. Pelo contrário, ele deve ser capaz de fazer uso dos significados já internalizados em sua estrutura cognitiva. Assim, de maneira progressiva, o aluno está diferenciando sua estrutura cognitiva, bem como, está fazendo a reconciliação integradora, identificando possíveis semelhanças e diferenças, de modo a (re) organizar seu conhecimento (MOREIRA, 2010).

Pode-se dizer com isso, que a construção do conhecimento por parte do aluno acontece de modo individualizado e correlacionado com seus conhecimentos prévios, sendo estes últimos, fundamentais para que a ancoragem de conteúdos ocorra de maneira efetiva e duradoura, constituindo-se em uma aprendizagem significativa.Segundo Moreira (2010), para que ocorra de fato a aprendizagem significativa, faz-se necessário as seguintes condições: o material a ser apresentado ao aluno deve ser potencialmente significativo; o aluno deve possuir em sua estrutura cognitiva subsunçores adequados; o aluno deve apresentar uma predisposição para aprender.

Quanto à primeira condição mencionada, deve-se considerar que o material tenha fundamento e significado lógico, de modo que represente algo e não esteja sujeito a incertezas, relacionando-se com os subsunçores do aprendiz. No que se refere à estrutura cognitiva do aprendiz, nesta, devem estar disponíveis os subsunçores específicos, os quais servem de âncora para o novo conhecimento. A disposição do aluno para a aprendizagem também é uma condição que requer muita atenção, pois, por mais que o material seja potencialmente significativo e que o aluno possua os subsunçores adequados, se ele não tiver interesse para aprender, a aprendizagem não terá significado (MOREIRA; MASINI, 2006).

Além das condições acima citadas, para que ocorra a aprendizagem significativa existem ainda princípios programáticos facilitadores de tal aprendizagem, dentre eles a diferenciação progressiva; a reconciliação integradora; a organização sequencial, e também algumas estratégias facilitadoras, tais como, organizadores prévios, diagramas V e os mapas conceituais. (MOREIRA, 2010).

A seguir, será discutida a elaboração de mapas conceituais, tendo como base os pressupostos apresentados por Moreira (1998, 2006).

3.1 Mapas conceituais

De um modo geral, pode-se dizer que mapas conceituais, ou mapas de conceitos, são diagramas que apresentam relações entre determinados conceitos. Cabe ressaltar, que embora incluam setas, esses não devem ser confundidos com fluxogramas nem com organogramas.

Na visão de Masini e Moreira (2006), os mapas conceituais devem, de algum modo, apresentar reflexões acerca das hierarquias existentes entre conceitos de um assunto ou até mesmo de uma disciplina da grade curricular. A função dos mapas conceituais não é a de classificar conceitos, mas sim relacionar e hierarquizar os mesmos.

Os autores acima mencionados ainda consideram que os mapas conceituais podem ser construídos em qualquer uma das áreas do conhecimento e também por estudantes, já desde as séries iniciais, até o nível de pós-graduação.

São múltiplas as maneiras de se traçar um mapa conceitual, ou seja, não existe um único mapa conceitual considerado correto para um assunto em questão. Conforme lembra Moreira (2006, p. 46) "um mapa conceitual deve ser sempre visto com 'um mapa conceitual', não como, 'o mapa conceitual' de um determinado conjunto de conceitos". Nesse sentido, os mapas conceituais devem ser interpretados como uma das inúmeras formas de representação de dada estrutura conceitual.

No que se refere à hierarquização dos conceitos dispostos em um mapa conceitual, os conceitos mais amplos e inclusivos devem aparecer no topo do mapa, enquanto os conceitos subordinados ordenam-se, de cima para baixo no eixo vertical, até que na base do mapa figurem os conceitos mais específicos e também os exemplos conforme se observa na figura 1 a seguir:

Figura 1- Modelo de mapeamento conceitual.

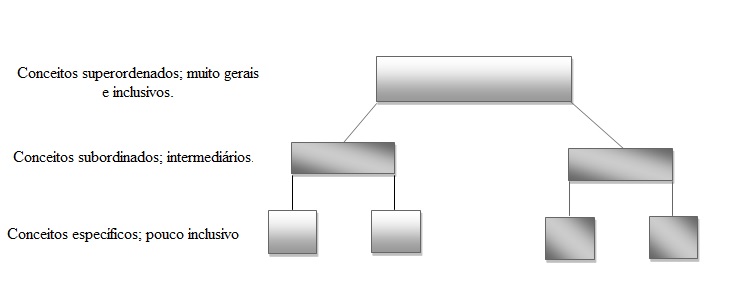
Fonte: Moreira (2006,p.47)

Para sugerir relações entre conceitos são usadas linhas, que têm a função de conectar vários conceitos. Uma ou duas palavras-chave escritas sobre essas linhas são consideradas suficientes para explicitar essas relações. No entender de Moreira (1998), dois conceitos adicionados as palavras-chave formam uma proposição, a qual evidencia o significado da relação conceitual.

Ainda segundo Moreira (1998), é importante a utilização de palavras-chave na construção de mapas de conceitos, contudo, esse recurso não os torna autoexplicativos. Nesse sentido, os mapas conceituais devem ser explicados por seus autores. Ao fazer a explanação de um mapa conceitual, o indivíduo que o elaborou externaliza significados, constituindo desse modo, um dos maiores valores do trabalho com os mapas conceituais, contribuindo assim, para a ocorrência de uma aprendizagem significativa.

4. Proposta de utilização de mapas conceituais no Ensino de estatística básica

Partindo da premissa de que os mapas conceituais são instrumentos facilitadores de aprendizagem de conceitos, considera-se que o uso dos mesmos no ensino dos conteúdos inerentes à Estatística, pode contribuir para que os alunos compreendam conceitos e informações mais complexas e relacionáveis entre si, ocorrendo assim, uma aprendizagem significativa.

Como exemplo de utilização de mapas conceituais no ensino de Estatística, elaborou-se diagramas referentes aos conteúdos básicos relacionados à Estatística Descritiva. Os conteúdos contemplados nos mapas conceituais aqui apresentados estão definidos pelas Diretrizes Curriculares Estaduais do Estado do Paraná (2008) a serem trabalhados no 7º ano do Ensino Fundamental. Porém, os mesmos podem ser trabalhados ao longo dos anos finais do Ensino Fundamental.

Na prática, os exemplos aqui apresentados têm como objetivo promover uma visão geral prévia do conteúdo estatístico a ser ministrado, porém, cabe ao professor explicar aos seus alunos os mapas e a sua finalidade. O professor deve ainda, advertir os alunos que um mapa conceitual pode ser traçado de várias maneiras e estimula-los a traçar seus próprios mapas à medida que cada conteúdo for trabalhado, permitindo assim, uma maior integração, reconciliação e diferenciação de significados de conceitos (MOREIRA, 1998). Segundo o referido autor, o professor não deve esperar que o aluno desenvolva um mapa conceitual 'correto' de um certo conteúdo, mas sim, que apresente 'o seu mapa', pois "o importante não é se esse está certo ou não, mas sim se ele dá evidências de que o aluno está aprendendo significativamente o conteúdo" (MOREIRA, 1998, p. 150).

Na figura 2 a seguir, pode-se observar um mapa conceitual elaborado para o ensino das variáveis estatísticas.

Figura 2- Mapa conceitual para o ensino de variáveis estatísticas.

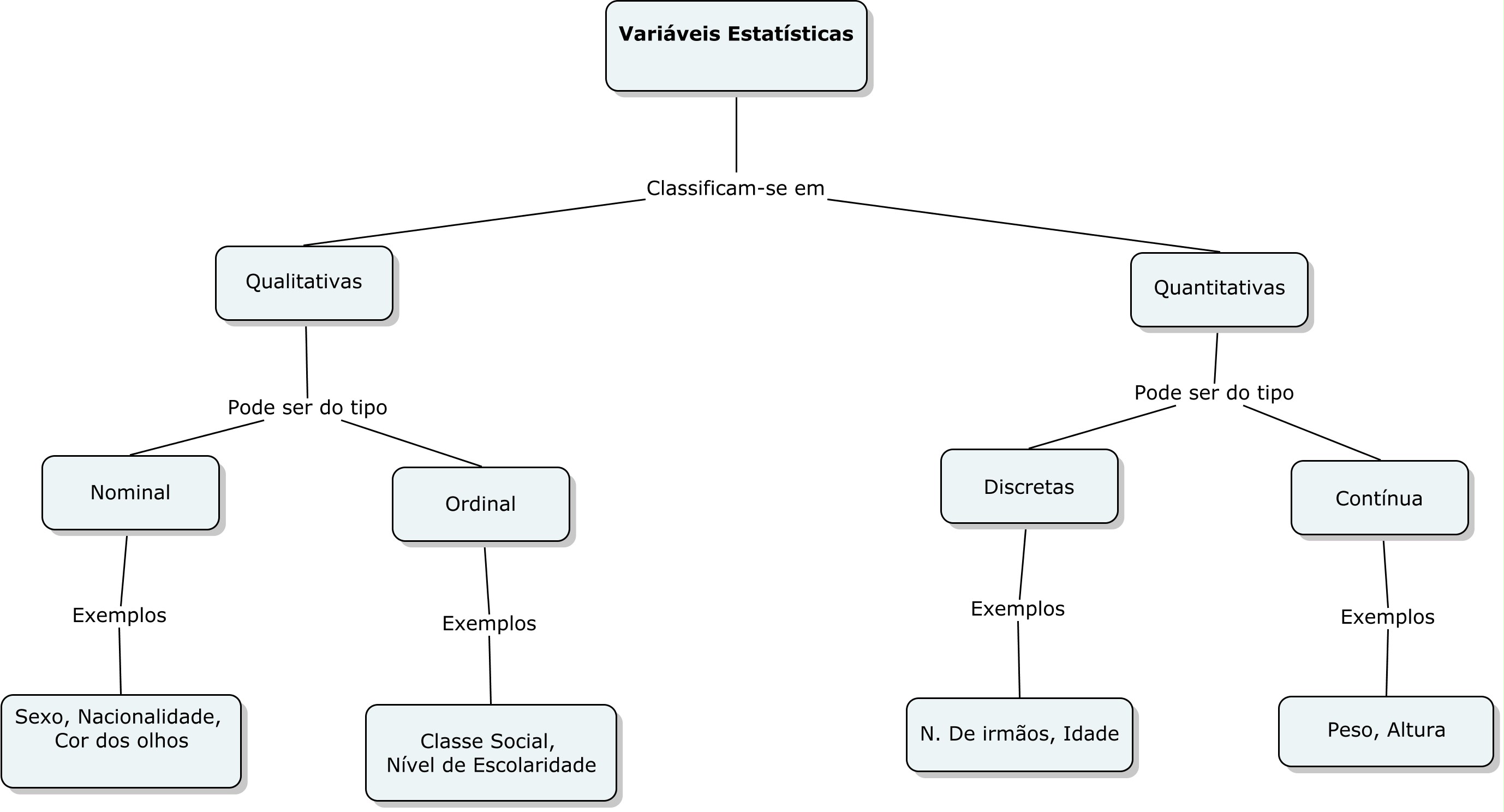
Fonte: Autoria própria.

A figura 2 apresentada serve para iniciar o estudo referente às variáveis estatísticas. Em Estatística, cada característica pesquisada é denominada variável. De acordo com a natureza, as variáveis classificam-se em qualitativas (também chamada de categorizada) e quantitativas (também denominada de numérica).Para uma variável qualitativa os resultados são categorias. Essas categorias podem assumir um tipo de ordenação. Nesse caso, a variável é chamada de variável qualitativa nominal. Como por exemplo, as variáveis gênero, nacionalidade, esporte preferido, dentre outros. Um outro tipo de variável é a chamada variável qualitativa ordinal. Por exemplo, nível de escolaridade (Ensino Fundamental, Ensino Médio, Ensino Superior, Pós-graduação).

Em relação à variável quantitativa, os resultados fornecem quantidades. Assim, se essa variável é passível de ser contada, ela recebe o nome de variável quantitativa discreta. Como exemplo, tem-se a variável número de irmãos, e a variável idade (em anos completos), dentre outras. Quando a variável é o resultado de uma mensuração, podendo assumir qualquer valor real em um determinado intervalo, ela chama-se variável quantitativa contínua. Ainda como exemplo, tem-se as variáveis peso e altura, dentre outras (CAZORLA; OLIVEIRA, 2010).

A figura 3, a seguir, foi elaborada com o objetivo de mostrar que os dados estatísticos podem ser representados de maneira gráfica e/ou tabular.

Figura 3- Mapa conceitual para o ensino de representação de dados.

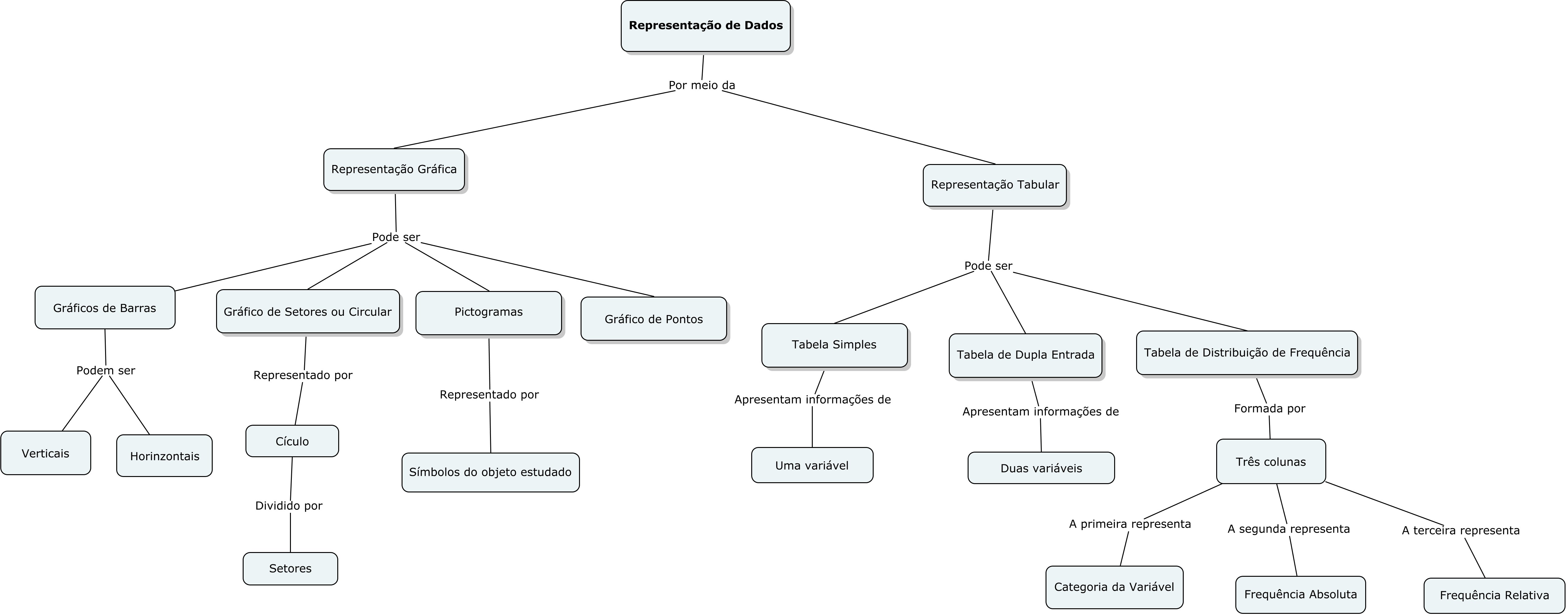
Fonte: Autoria própria.

A Figura 3 apresentada serve para distinguir as formas de representação de dados, as quais podem se dar por meio de gráficos e tabelas. Os gráficos, por sua vez, permitem a leitura e a compreensão do comportamento de uma variável ou das relações existentes entre variáveis.Os gráficos mais comuns são os de barras, os de setores, os de pontos e os pictogramas.

Os gráficos de barras podem ser verticais ou horizontais. No que diz respeito ao gráfico de barras verticais ou de colunas, seu objetivo é mostrar as diferenças de frequências absolutas ou relativas, ou de valores de uma ou mais variáveis. No que se refere ao gráfico de barras horizontais, estes apresentam a mesma função que o gráfico de colunas, sendo recomendado seu uso quando as legendas das categorias são mais longas (VENDRAMINI;CAZORLA;SILVA, 2009). Quanto ao gráfico de setores ou circular, esse é representado por um círculo, o qual é dividido em setores, onde a área destes é proporcional à sua respectiva frequência (CAZORLA; OLIVEIRA, 2010). Em relação aos pictogramas, nesses tipos de gráficos são usados símbolos para representar o objeto de estudo. São muito utilizados para representar variáveis categorizadas quando se trabalha com alunos que ainda não conhecem o plano cartesiano (CAZORLA; OLIVEIRA, 2010). Nos gráficos de pontos é feita a substituição da barra por pontos, os quais ficam empilhados sobre a reta numérica quando os valores das variáveis se repetem. Neste tipo de gráfico não é colocado o eixo vertical, pois sua função é mostrar apenas o formato e os padrões. (KATAOKA; HERNANDEZ, 2010).

A representação de dados feita de maneira tabular, deve ser organizada de forma clara e conter todos os elementos essenciais a sua compreensão, sendo que não há necessidade de texto para serem compreendidas. Os principais tipos de tabelas são: tabelas simples, tabelas de distribuição de frequência e tabelas de dupla entrada. As tabelas simples são aquelas que apresentam informações de apenas uma variável e, as tabelas de dupla entrada apresentam informações relacionadas a duas variáveis (WALICHINSKI, 2012b).As tabelas de distribuição de frequência (TDF), geralmente, são formadas por três colunas: a primeira representa as categorias da variável, a segunda coluna representa o número de observações em cada uma das categorias (frequência absoluta), e a terceira que representa a distribuição percentual (frequência relativa) (CAZORLA; SANTANA, 2009).

Figura 4 - Mapa conceitual para o ensino de medidas de tendência central.

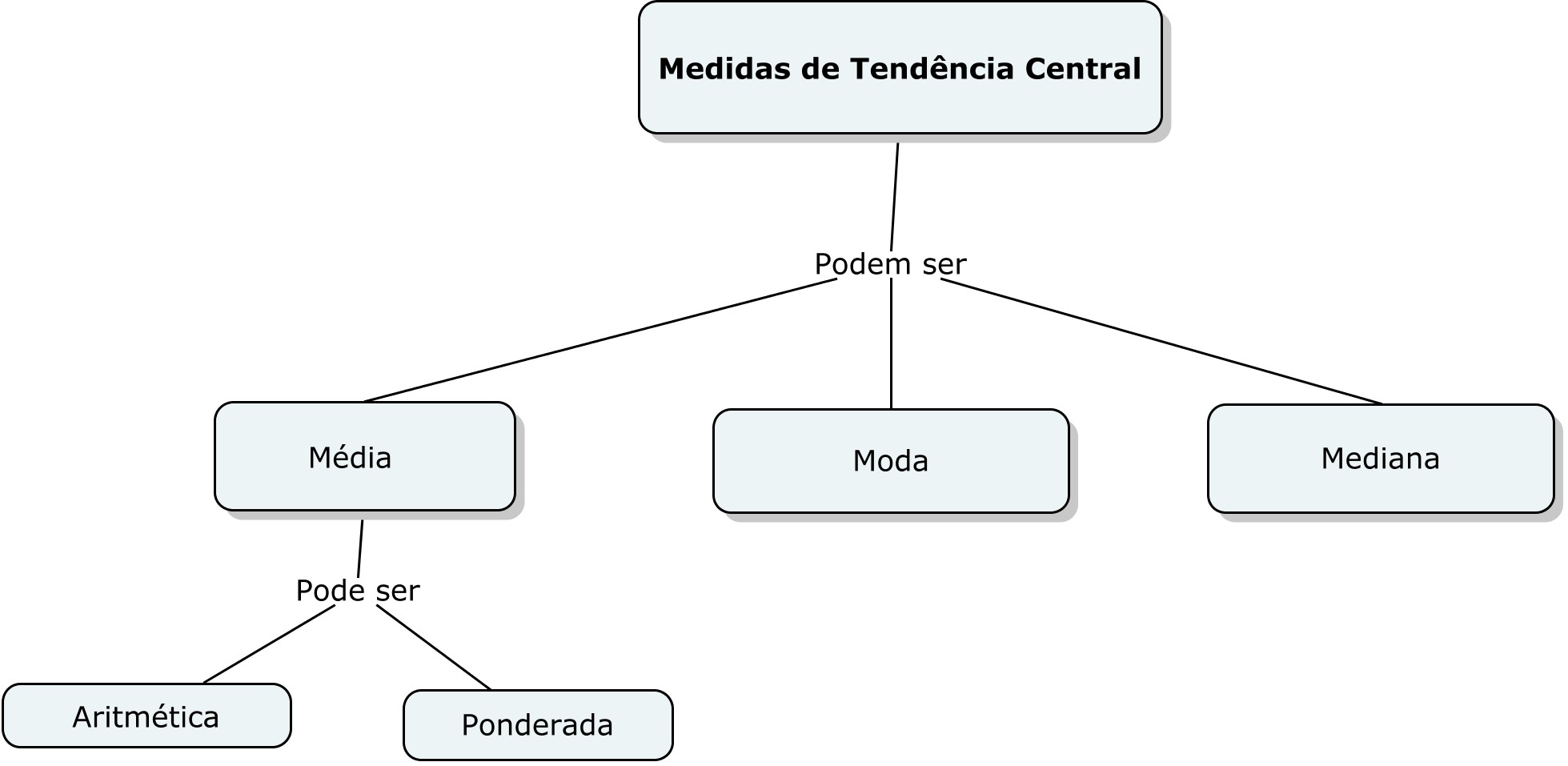
Fonte: Autoria própria.

A figura 4 representa as medidas de tendência central, que podem ser: média, moda e mediana. A média pode ser de dois tipos: média aritmética e média ponderada. A média aritmética é amplamente utilizada na Estatística e tem a função de representar por meio de um único número o valor de uma variável para um conjunto de dados. Para a média ponderada, os valores da variável têm pesos ou ponderações diferentes. (CAZORLA; OLIVEIRA, 2010). A moda por sua vez, é o valor ou a categoria que se repete com maior frequência. Algumas variáveis podem ter mais de uma moda, nesse caso, elas são chamadas de multimodais. (CAZORLA; OLIVEIRA, 2010). Essa medida de tendência central é utilizada "quando desejamos obter o valor mais típico de uma amostra" (GITIRANA et al., 2010, p. 109). Já a mediana, é o valor que divide um conjunto de dados (ordenados) em duas partes iguais. Segundo Cazorla e Oliveira (2010), o conceito de mediana é realizada de forma intuitiva.

5. Considerações finais

Atualmente, não há dúvidas acerca da relevância do conhecimento estatístico para a formação plena do cidadão, sendo consenso que o trabalho com os conteúdos estatísticos deve estar baseado em situações significativas aos alunos, de modo a permitir que os mesmos compreendam conceitos e informações mais complexas e relacionáveis entre si.

Sabendo-se então, que a principal função dos mapas conceituais seja apresentar relações entre conceitos, nesse ensaio teórico, apresentou-se uma proposta para o uso de mapas conceituais como estratégia facilitadora de uma aprendizagem significativa para o ensino de conceitos referentes às variáveis estatísticas, à representação de dados e, às medidas de tendência central. Tendo em vista que os mapas conceituais não são autoexplicativos, apresentou-se ainda um aporte teórico sobre esses conceitos.

Entende-se que essa proposta pode auxiliar os docentes a orientar os alunos na construção de esquemas mentais para maior compreensão do conceito de variável; na identificação dos diferentes tipos de representação de dados e na diferenciação entre as medidas de tendência central. Isso possibilitará também uma escolha mais adequada para análise de dados. Nesse sentido, acredita-se que a teoria da aprendizagem significativa, idealizada por David Ausubel, pode contribuir para a eficácia do processo de ensino e aprendizagem de conceitos estatísticos.

Embora os conceitos abordados nesse estudo estejam previstos, segundo a proposta curricular do Estado do Paraná, a serem trabalhados com alunos do 7° ano do Ensino Fundamental, entende-se que essas atividades podem ser aplicadas/adaptadas a qualquer turma dos anos finais do Ensino Fundamental. Assim, espera-se que esse ensaio possa incentivar os professores a trabalharem com os conceitos estatísticos de maneira significativa em suas aulas.

6. Referências

CAMPOS, C. R. ; JACOBINI, O. R. ; WODEWOTZKI, M. L. L. ; FERREIRA, D. H. L. Educação Estatística no contexto da Educação Crítica. Bolema. Boletim de Educação Matemática (UNESP. Rio Claro. Impresso), v. 24, p. 473-494, 2011.

CAMPOS, C. R.; WODEWOTZKI, M. L. L.; JACOBINI, O. R. Educação estatística: teoria e prática em ambientes de modelagem matemática. Belo Horizonte (MG): Autêntica, 2011.

CAZORLA, I. ; KATAOKA, V. Y. ; SILVA, C. B. da . Trajetórias e perspectivas da educação estatística no Brasil: um olhar a partir do GT 12. In: LOPES, C.E. ; COUTINHO, C.de Q. e S. ; ALMOULOUD, S. A. (Orgs.) Estudos e reflexões em educação estatística. Campinas (SP): Mercado de letras, 2010.

CAZORLA, I. ; OLIVEIRA, M. S. Para saber mais. In: CAZORLA, I.; SANTANA, E. (Org.) Do tratamento da informação ao letramento estatístico. Itabuna (BA): Via Litterarum, 2010.

CAZORLA, I.; SANTANA, E.R.S. Tratamento da informação para o ensino fundamental e médio. 2. ed. Itabuna (BA): Via Litterarum, 2009.

GAL, I.(2002). Adult's statistical literacy : meanings, components, responsabilities. InternationalStatisticalReview, v. 70, n. 1, p. 1-25.

GITIRANA, V.; et al. Média aritmética no ensino fundamental. In: LOPES, C.E. ; COUTINHO, C. de Q. e S. ; ALMOULOUD, S.A. (Orgs.) Estudos e reflexões em educação estatística. Campinas (SP): Mercado de Letras, 2010.

GOMES, A. P. et al. A educação médica entre mapas e âncoras: a aprendizagem significativa de David Ausubel, em busca da arca perdida. Revista Brasileira de Educação Médica, v.29, nº 1, Rio de Janeiro, 2008.

KATAOKA, V. Y. ;  HERNANDEZ, H. Sequência de ensino 1: perfil da turma. In: CAZORLA, Irene; SANTANA, Eurivalda (Orgs.) Do tratamento da Informação ao letramento estatístico. Itabuna (BA): Via Litterarum, 2010.

LOPES, C.E. Os desafios para educação estatística no currículo de matemática. In: LOPES, C. E. ; COUTINHO, C.de Q. e S. ; ALMOULOUD, S. A. (Orgs.) Estudos e reflexões em educação estatística. Campinas (SP): Mercado de letras, 2010.

MOREIRA, M. A. Mapas Conceituais e Aprendizagem Significativa. Cadernos de Aplicação. V. 11, n. 2, p. 143-156, 1998.

MOREIRA, M. A. A teoria da aprendizagem significativa e sua implementação em sala de aula. Brasília, DF: UnB- Universidade de Brasília, 2006.

MOREIRA, M. A. Aprendizaje Significativo Crítico. 2.ed: ISBN 85-904420-7-1, 2010.

MOREIRA, M.A; MASINI, E. A. F. Aprendizagem significativa: a teoria de David Ausubel. 2.ed. São Paulo: Centauro Editora, 2006.

PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica: Matemática. Paraná: SEED/DEB, 2008.

VENDRAMINI, Claudete M. M. ; CAZORLA, Irene M. ; SILVA, Claúdia B. Normas para a apresentação de informações estatísticas no estilo editorial. In: SABADINI, Aparecida Z. P.; SAMPAIO, Maria I. C. ; KOLLER, Sílvia H. (Orgs.) Publicar em psicologia: um enfoque para a revista científica. São Paulo (SP): Associação Brasileira de Editores Científicos de Psicologia / Instituto de Psicologia da Universidade de São Paulo, 2009.

WALICHINSKI, D. Contextualização no ensino de estatística: uma proposta para os anos finais do ensino fundamental. Dissertação (Mestrado) – Pós-Graduação em Ensino de Ciência e Tecnologia. Universidade Tecnológica Federal do Paraná. Ponta Grossa, 2012a.

WALICHINSKI, D. Sequência de ensino contemplando a estatística nos anos finais do ensino fundamental segundo pressupostos da contextualização. Produto Técnico (Mestrado Profissional) – Pós-Graduação em Ensino de Ciência e Tecnologia. Universidade Tecnológica Federal do Paraná. Ponta Grossa, 2012b.

1 Universidade Tecnológica Federal do Paraná - Brasil – eishikawa@utfpr.edu.br
2 Universidade Tecnológica Federal do Paraná - Brasil – guata39@gmail.com

3 Universidade Tecnológica Federal do Paraná - Brasil – dani.walichinski@gmail.com

4 Universidade Tecnológica Federal do Paraná - Brasil - nilceia@utfpr.edu.br
5 Universidade Tecnológica Federal do Paraná - Brasil - siumara@utfpr.edu.br