1. Introdução
O método do gerenciamento de restrições é composto por um conjunto de princípios e conceitos idealizados pelo físico israelense Eliyahu Goldratt, nos anos 1980, conhecido como Teoria das Restrições (TOC – Theory of Constraints), um método novo de administração da produção. O sucesso de sua teoria em algumas empresas fez com que outras se interessassem em aprender a técnica. Assim Goldratt decidiu repassar o seu conhecimento e escreveu um livro contando sobre sua teoria, chamado de "A Meta (The Goal)" (Goldratt; Cox, 1993).
Como uma teoria de gestão, a TOC foi inicialmente aplicada em sistemas industriais, com o objetivo de obter uma melhoria contínua de seus processos. Apesar da teoria das restrições ter nascido no setor industrial, sua filosofia pode ser empregada em diferentes organizações (Oliveira et al., 2006).
Existem duas premissas em sua abordagem. A primeira é considerar a empresa como um sistema cujo sucesso ou fracasso depende da forma como diferentes processos interagem entre si. A segunda é a de que uma restrição é qualquer coisa que limite o sistema de atingir sua meta. Sendo assim, todo sistema deve ter pelo menos uma restrição ou fator limitante.
Uma restrição não é boa nem má. Ela existe e deve ser gerenciada (Goldratt, 1993). De fato, o reconhecimento da existência de um fator limitante é uma excelente oportunidade para a melhoria, pois permite o foco na identificação e gerenciamento das restrições.
Segundo a Teoria das Restrições, toda empresa é um sistema tangível cujo desempenho vai depender da forma como interagem seus diferentes processos. A restrição pode ser identificada pela existência de filas de espera ou por tempos de processamento longos (Goldratt, 1992).
As filas se formam em decorrência do aumento dos consumidores e da incapacidade do sistema em atender a essa demanda. Assim, através de técnicas de simulação, busca-se encontrar um ponto de equilíbrio que satisfaça os clientes e seja viável economicamente para o provedor do serviço (Arenales, 2007).
Segundo Banks (1998), simulação é uma técnica de solução de um problema pela análise de um modelo que descreve o comportamento de um sistema usando um computador digital. A simulação de um modelo permite entender a dinâmica de um sistema assim como analisar e prever o efeito de mudanças que se introduzam no mesmo. É uma representação próxima da realidade, e será tanto mais real quanto mais características significativas do sistema seja capaz de representar. Por outro lado, o modelo deve ser simples, de forma que não se torne demasiado complexo para se construir, mas ao mesmo tempo o modelo deve ser o mais fiel possível ao sistema real (Fernandes et al., 2006).
A chegada de clientes, em um restaurante, em grupos pode incrementar o tamanho das filas drasticamente em um pequeno intervalo de tempo. Uma má gestão destas filas conduzem a uma insatisfação do cliente. Diante do exposto, este trabalho teve por objetivo aplicar princípios da teoria das restrições e técnicas de simulação na gestão da dinâmica operacional de um pequeno restaurante universitário.
2. Fundamentação Teórica
2.1. Simulação Computacional
A simulação tem sido cada vez mais aceita e empregada como uma técnica que permite aos analistas dos mais diversos seguimentos verificarem ou encaminharem soluções com a profundidade desejada, aos problemas com os quais lidam diariamente. A simulação computacional permite que estudos sejam realizados sobre sistemas que ainda não existem, levando ao desenvolvimento de projetos eficientes antes que qualquer mudança física tenha sido iniciada (Kelton et al., 1998).
Segundo Prado (2010), existem duas etapas para o estudo de simulação de sistemas. Na primeira o analista deve construir um modelo, fornecer alguns dados e obter outros que sejam idênticos ao sistema que está sendo estudado. A segunda consiste na mudança do modelo, para que com base nos resultados obtidos, realizem-se análises, gerando recomendações e conclusões.
A simulação é mais fácil de aplicar que os modelos analíticos, que por sua vez devem ainda ser muito simplificados para tornarem-se viáveis matematicamente. Por fim, podem ser quase tão detalhados como os sistemas reais, permitindo realizar ensaios num cenário muito similar ao real sem o ônus e o desgaste de ter de interferir na rotina dos sistemas reais. Permite também um estudo detalhado de todas as operações e características do sistema (Law; Kelton, 2000).
Freitas Filho (2008) afirma que o uso da simulação deve ser considerado quando uma ou mais das sete condições citadas a seguir, existirem:1) Não existe formulação matemática completa para o problema; 2) Não há solução analítica para o problema; 3) A obtenção de resultados é mais fácil de alcançar com a simulação do que com o modelo analítico; 4) Não existe habilidade pessoal para a resolução do modelo matemático por técnicas analíticas ou numéricas; 5) É necessário observar o processo desde o início até os resultados finais, mas não necessariamente detalhes específicos; 6) A experimentação no sistema real é difícil ou até mesmo impossível; 7) É interessante observar longos períodos de tempo ou alternativas que os sistemas reais ainda não possuem.
Segundo Law e Kelton (2000), as principais vantagens da simulação advêm do fato que um modelo criado pode ser utilizado inúmeras vezes, o qual não depende da disponibilidade do sistema real para a realização de ensaios, nem incorre em custos para executar os experimentos. Esse modelo pode conter simplificações com relação aos sistemas reais para que facilitem a modelagem e torne mais fácil a compreensão dos parâmetros abordados, desde que os elementos desprezados não interajam com os parâmetros estudados com relação aos resultados a serem avaliados.
Como desvantagens, Law e Kelton (2000) citam que a construção de modelos exige treinamento e experiência prévia e nem sempre a variabilidade de um sistema é bem captada e modelada, podendo levar a resultados equivocados. Entretanto, algumas soluções, tais como introdução de geradores de números aleatórios, podem ajustar o modelo de forma a representar bem a variabilidade. Ainda, destacam que a construção de modelos consome muito tempo. Tentativas de reduzir este tempo por via de simplificação do modelo podem levar a resultados insatisfatórios.
2.2. Teoria das Restrições
Segundo Goldratt (1998) o administrador, para proteger os ganhos, precisa saber em que enfocar e como enfocar. O processo de focalização, em cinco etapas, é uma metodologia que possibilita determinar como explorar os gargalos para obter melhorias no desempenho da organização. Os passos por ele descritos encontram-se ilustrados na Figura 1.
Figura 1. Fluxograma descritivo das etapas de avaliação de restrições.
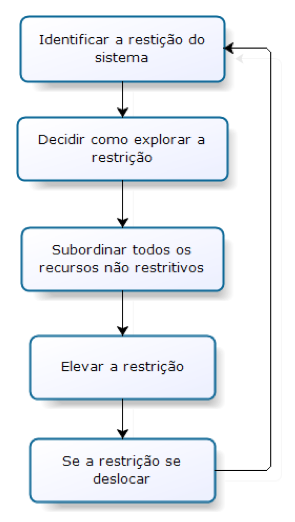
Fonte: Adaptado de Goldratt, (1998).
No primeiro passo, onde se realiza a identificação da restrição do sistema, deve-se observar qual é o recurso que restringe o desempenho do sistema, pode ser identificado através da existência de filas de espera ou por tempos de processamento longos.
A seguir deve-se decidir como explorar a restrição, ou seja, uma vez identificado o gargalo, existem duas maneiras de melhorar o seu desempenho: Adicionando mais capacidade ao recurso ou gerenciando melhor o recurso.
Depois disso então se deve subordinar todos os recursos não restritivos. Desde que o desempenho total seja comandado pelas restrições, deve-se ao menos fazer com que estas sejam alimentadas pelos demais recursos, ou seja, o seu nível de utilização não será determinado pelo seu potencial individual, mas sim pelo sistema. Não se pode medir a capacidade de um recurso isoladamente, pois a verdadeira capacidade produtiva depende de onde o recurso está na fábrica. Portanto, as não restrições devem fornecer tudo o que as restrições precisam consumir e nada a mais (Oliveira et al., 2006).
Assim, estando a situação sob controle, deve-se elevar a capacidade da(s) restrição(ões) como forma de reduzi-la(s) ou suprimi-la(s). E, por fim, se a restrição se deslocar não permitir que a inércia se instale e retornar ao primeiro passo. Não se pode permitir que a inércia se instale e se transforme numa restrição do sistema. O ambiente está em constante mudança. Uma solução tende a se deteriorar ao longo do tempo. A teoria das restrições é um processo de aprimoramento contínuo.
2.3. O Software Arena
O software Arena® é um ambiente gráfico integrado de simulação, que contém inúmeros recursos para modelagem, animação, análise estatística e análise de resultados. A plataforma de simulação Arena® possui as seguintes ferramentas (Prado, 2010):
- Analisador de dados de entrada (Input Analyzer);
- Analisador de resultados (Output Analyzer);
- Analisador de processos (Process Analyzer).
Este software é composto por um conjunto de blocos (ou módulos) utilizados para se descrever uma aplicação real e que funcionam como comandos de uma linguagem de programação. Os elementos básicos da modelagem em Arena® são as entidades que representam as pessoas, objetos, transações, etc, que se movem ao longo do sistema; as estações de trabalho que demonstram onde será realizado algum serviço ou transformação, e por fim, o fluxo que representa os caminhos que a entidade irá percorrer ao longo de estações (Kelton et al., 1998).
3. Material e Métodos
O restaurante self-service é um dos empreendimentos alimentícios característicos do mundo moderno. Vivendo a correria diária dos grandes centros urbanos, os consumidores estão exigindo comida pronta, variada, nutritiva, bem elaborada, na quantidade escolhida, servida em ambiente confortável e com preço acessível.
De origem inglesa, a palavra self-service significa auto-serviço, dispensando o atendimento prestado por garçons. O sistema de pesagem utilizado nos restaurantes self-services por quilo tem conquistado a simpatia do consumidor, permitindo ao cliente escolher os alimentos para sua refeição, na quantidade desejada (Senai, 2010).
O restaurante, objeto deste estudo, oferta refeições servidas a peso, no sistema self-service, compreendendo saladas, pratos quentes e sobremesas, incluindo o fornecimento de bebidas.
O processo inicia-se no momento que os clientes chegam ao restaurante. Na sequência dirigem-se a mesa de buffet com capacidade para 10 clientes ao mesmo tempo. A seguir, deslocam-se para estação de pesagem. Nesta estação acontece o pedido da bebida e a pesagem, através de uma balança eletrônica, dos alimentos que serão consumidos. Depois de pesar, os alimentos, os clientes se deslocam para as mesas do restaurante (310 lugares). Após o almoço, alguns clientes se dirigem ao caixa para pagamento. Observa-se que, no momento da pesagem, os nomes dos clientes que pagam por mês, são anotados pelo funcionário que atende na estação de pesagem.
O sistema analisado, neste trabalho, é apresentado através do modelo conceitual (IDEF-SIM) na Figura 2.
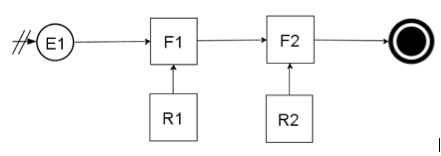
Figura 2. Modelo conceitual do sistema analisado.
Onde E1 corresponde a Chegada dos Clientes ao restaurante; F1 processo de se servir na Mesa do Buffet; F2 Processo de pesagem; R1 Recurso – Mesa de Buffet com 10 lugares e R2 Recurso – Balança.
O conceito chave da TOC refere-se à restrição, ou seja, o fator que restringe a atuação do sistema como um todo. As restrições físicas ou de recursos são oriundas de elementos necessários à operacionalização da empresa, tais como pessoas, equipamentos, dispositivos, instrumentos, espaço físico, mercado, fornecedor, máquinas, materiais, entre outros.
Segundo Dettmer (1995) podem ser encontradas várias restrições, porém os esforços de melhoria devem ser concentrados na mais crítica. A restrição mais crítica, do restaurante, está no espaço físico destinado a fila de clientes da balança, que pode comportar somente 8 clientes.
3.1 Coleta De Dados
No planejamento, da coleta de dados, concluiu-se que seria necessário determinar as seguintes variáveis: tempos entre chegadas dos clientes (TEC); tempos que os clientes levam, para servirem-se, na mesa de buffet (TFB) e tempos de atendimento na balança (TFBL).
Estes dados foram analisados com a ferramenta Input analyzer (analisador de dados de entrada) do software Arena®. Segundo Prado (2010) esta ferramenta permite analisar dados reais do funcionamento do processo e escolher a melhor distribuição estatística que se aplica a eles.
A simulação da dinâmica operacional do restaurante foi realizada com o software Arena®, e os resultados analisados nas ferramentas Output Analyzer e Process Analyzer.
Na seguinte seção serão detalhados os dados coletados e o tratamento dado a eles visando garantir a sua consistência para utilização no modelo.
3.2 Número De Replicações
Segundo Freitas Filho (2008), de uma maneira geral, a coleta de dados para a composição de uma amostra a partir da simulação de um modelo pode ser realizada de duas formas.
A primeira forma seria fazer uso das observações individuais dentro de cada replicação. Por exemplo, pode-se simular o modelo do restaurante e utilizar o tempo que cada cliente esperou na fila da mesa do buffet para realizar uma estimativa do tempo médio de espera na fila. Neste caso, o tamanho da amostra será igual à quantidade de clientes que passaram pela fila ao longo do período simulado.
A segunda maneira de gerar a amostra seria realizar n simulações (replicações). Assim, cada replicação gera um elemento para a amostra. Uma vez que estamos lidando com um sistema terminal no qual as condições iniciais e o período de simulação são fixos, a melhor maneira de garantir que os valores da amostra sejam estatisticamente independentes é obtê-los a partir de replicações independentes.
Neste trabalho, o número de replicações (n*) foi obtido através da seguinte expressão (Montgomery, 2005):

onde:
n - número de replicações já realizadas;
h - semi-intervalo de confiança já obtido; e
h* - semi-intervalo de confiança desejado
3.3. Validação Do Modelo
A validação tem por objetivo proceder à comparação de valores de variáveis geradas pelo modelo com os obtidos do sistema real (Sargent, 2009). Na execução do procedimento de validação, para o sistema em estudo, foi: (i) realizada uma comparação de médias por meio de análise de variância (ANOVA); (ii) calculado o erro médio estimado (Menner, 1995):

onde:
SE – erro médio estimado;
SR – valor obtido a partir do sistema real;
MD – média dos valores gerados pelo modelo; e
GLR – grau de liberdade considerando o número de replicações do modelo.
A análise de variância é um teste estatístico amplamente difundido entre os analistas, e visa fundamentalmente verificar se existe uma diferença significativa entre as médias de dois ou mais grupos (Montgomery, 2005).
3.4. Tamanho da Amostra
O tamanho de cada uma das três amostras, cronometradas neste trabalho, foi obtida, para um nível de confiança de 95%, através da seguinte expressão:

onde:
nA- número de indivíduos da amostra;
Zα⁄2– valor crítico que corresponde ao grau de confiança desejado;
S- desvio padrão;
E- erro máximo estimado.
4. Resultados e Discussão
Na Tabela 1 são apresentados os valores, da análise exploratória, dos dados coletados no restaurante.
Tabela 1. Análise exploratória dos dados coletados no restaurante.
Parâmetro analisado |
TEC |
TFB |
TFBL |
Pontos |
157 |
100 |
154 |
Média |
11,90 s |
124,69 s |
9,16 s |
Mediana |
7,09 s |
115.7 s |
8,00 s |
Mínimo |
0,03 |
45,5 |
5 |
Máximo |
46,1 |
245,7 |
21,1 |
1 Quartil (Q1) |
2,09 s |
91,00 s |
6,06 s |
3 Quartil (Q3) |
17,04 s |
152,1 s |
12,00 s |
Desvio Padrão |
11,66 s |
50,21 s |
3,88 s |
Coeficiente de Variação |
98,17% |
40,27% |
42,41% |
Observa-se, através dos dados apresentados na Tabela 1, que a variável Tempo no Buffet (TFB) apresentou a maior mediana e a maior média entre os dados coletados no restaurante. Já os coeficientes de variação (98,17%, 40,27% e 42,41%) para as três variáveis coletadas apresentam de acordo com os conceitos descritos por Pimentel (2000), uma dispersão alta, possuindo uma elevada variabilidade em relação à média.
Após a análise exploratória, realizou-se à análise de correlação entre os dados, ou seja, verificou se há dependência entre os valores das amostras. Na Figura 3 é apresentado, como exemplo, o gráfico de dispersão dos tempos entre chegadas dos clientes no restaurante onde se pode observar que não houve correlação entre as observações da amostra.
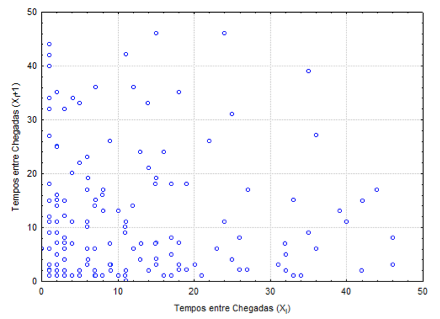
Figura 3. Gráfico de dispersão –
Tempos entre chegadas de clientes (TEC: Segundos).
4.1. Tratamento de Dados
Inicialmente, os dados foram plotados em forma de boxplots (Figura 4) para uma análise preliminar do comportamento das observações. A seguir, aplicou-se a técnica de identificação de outliers (valores fora da normalidade) apresentada na Tabela 2 (Marroco, 2003).
As razões mais comuns para o surgimento desses valores são os erros na coleta de dados ou eventos raros e inesperados. Os outliers considerados como extremos só foram descartados, das amostras, depois de uma análise criteriosa de suas causas. Os valores julgados como possíveis de ocorrer foram mantidos nas amostras.
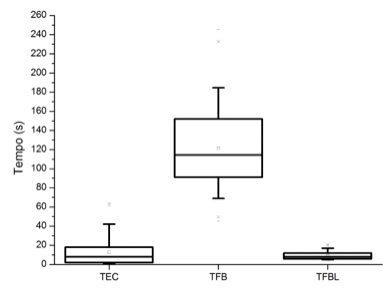
Figura 5. Boxplots dos tempos coletados no sistema.
-----
Tabela 2. Identificação de outliers.

Onde Q1 e Q3 são, respectivamente, os valores do primeiro e terceiro quartis, assim a amplitude entre inter-quartil "A" é calculada pela diferença: A=Q3-Q1.
Após a utilização da técnica de identificação dos outliers, o passo seguinte foi determinar as curvas de distribuição teórica de probabilidades que melhor representem o comportamento estocástico do sistema em estudo, através da ferramenta Input Analyzer do Arena®.
Como os p-values dos testes de aderência: teste Chi Square e do teste Kolmogorov-Smirnof são maiores que o nível de significância adotado (0,1) (Chwif; Medina, 2007), concluiu-se que as distribuições, apresentadas na Tabela 3, são as expressões que melhor se adaptaram aos dados coletados no sistema.
Tabela 3. Distribuição de probabilidade.
Itens |
Distribuição |
Chi Square |
Kolmogorov-Smirnov |
TEC |
EXPO(11.9) |
p-value=0,524 |
p-value=0,120 |
TFB |
45+366*BETA(2.24,8.48) |
p-value=0,691 |
p-value=0,632 |
TFBL |
6+EXPO(4.16) |
p-value=0,353 |
p-value=0,734 |
4.2. Validadação do Modelo Implementado
A comparação entre a média obtida do sistema real com a média gerada pelo modelo para a variável Tempo na Fila da Balança (TQB) são apresentados na Tabela 4. Nesta tabela apresenta-se, também, o erro médio estimado (SE, em decimal).
Tabela 4. Dados do sistema real e do modelo.
Tempo na Fila da Balança - TQB |
||
Sistema Real |
Modelo Computacional |
Erro Médio Estimado |
11,42 |
11,5±0,7 |
0,014 |
Ao ser aplicado a análise de variância, através da ferramenta de análise de dados por meio do Software Assistat 7.6 Beta (Tabela 5), a 1% de significância, na comparação das média obtida a partir do sistema real e a gerada pelo modelo de simulação, para a variável Tempo na Fila da Balança, não foram constatadas diferenças estatísticas. Pode-se observar, através dos dados apresentados na Tabela 5, que F0 é menor que Fcrítico (F0= 0,00497 enquanto Fcrítico= 7,011399).
Tabela 5. Análise de variância.
Fonte da variação |
SQ |
GL |
QM |
F0 |
valor-P |
F crítico |
Coletas |
1075,93 |
70 |
15,37043 |
0,869797 |
0,71946 |
1,753665 |
Tempos (Reais x Simulados) |
0,087823 |
1 |
0,087823 |
0,00497 |
0,943999 |
7,011399 |
Erro |
1236,99 |
70 |
17,67129 |
|||
Total |
2313,008 |
141 |
Onde: SQ: Soma de Quadrados; GL: Graus de Liberdade; QM: Quadrado Médio.
Considerando as discussões apresentadas, pode-se afirmar que o modelo computacional presta-se para os objetivos propostos neste trabalho.
4.3. Metodologia Toc
Para explorar o gargalo, com o objetivo de melhorar o desempenho do sistema em estudo, seguiram-se os passos descritos na Figura 1. A restrição do sistema foi identificada, sendo que esta se encontra no espaço físico destinado, no restaurante, a fila de clientes da balança.
Para explorar a restrição do sistema, utilizar o elemento restritivo na sua máxima capacidade, decidiu-se aumentar a capacidade da mesa de buffet.
Sincronizou-se o recurso, capacidade da mesa de buffet, as decisões tomadas anteriormente. Esta sincronização, visando o aumento na capacidade da mesa de buffet, foi testada através da simulação computacional.
Ao se implementar os passos 2 e 3 obtém-se como resultado a elevação da capacidade do sistema pela redução da ociosidade do gargalo. Caso a restrição se desloque, deve-se retornar ao passo 1 e não permitir que a inercia se instale.
Através da introdução, no modelo atual, de recursos que comtemplem todo o restaurante, pode-se gerenciar as restrições, que podem se deslocar para outro recurso, e atuar de maneira efetiva no sentido de garantir a eficácia do fluxo desejado de clientes no restaurante.
4.4. Simulação
Para analisar os efeitos, do aumento da capacidade da mesa, sobre o número de clientes nas filas do buffet e da balança, construiu-se dois cenários:
− Cenário 1: Mesa de buffet para 10 Lugares (Cenário Atual);
− Cenário 2: Mesa de buffet para 12 Lugares;
Na Tabela 6 apresentam-se os resultados obtidos (valores máximos), da simulação do sistema em estudo, para os dois cenários. Observa-se que os resultados foram obtidos após 40 replicações. Este número de replicações foi definido, com nível de confiança de 95%, utilizando a ferramenta Output Analyzer do Arena®.
Tabela 6. Resultados de simulação.
Cenários |
Buffet |
Balança |
Fila do Buffet |
Fila da Balança |
Clientes Atendidos |
Cenário 1 |
10 |
1 |
19,92 |
5,60 |
270 |
Cenário 2 |
12 |
1 |
8,57 |
7,45 |
295 |
Observa-se, da Teoria das Restrições, que a utilização de um recurso não-gargalo não é determinado pelo sua disponibilidade, mas pela restrição do sistema. Portanto, para atender a restrição do sistema (8 clientes), pode-se aumentar a capacidade da mesa de buffet para atender 12 clientes ao mesmo tempo. Observa-se, também que em relação ao número de clientes atendidos, existe uma diferença de 25 clientes entre os dois cenários simulados no horário de almoço.
5. Considerações Finais
Neste trabalho utilizou-se os princípios da teoria das restrições e técnicas de simulação na gestão da dinâmica operacional de um pequeno restaurante do tipo self-service.
De acordo com os resultados das análises procedidas para a validação do modelo computacional implementado, foi possível concluir que o mesmo pode ser aplicado para simular a dinâmica operacional do restaurante.
Através dos resultados obtidos de simulação, notou-se que para aumentar o número de clientes atendidos no restaurante e acatar a restrição da fila da balança, deve-se utilizar uma mesa com capacidade para 12 lugares.
A aplicação da Teoria das Restrições e da simulação computacional gerou um conhecimento adicional à cerca do processo para todos os envolvidos e possibilitou, também, a identificação de oportunidades de melhorar o sistema de atendimento aos clientes, do restaurante estudado.
Referências Bibliográficas
ARENALES, M. Pesquisa Operacional. Rio de Janeiro: Elsevier, 2007. 524 p.
BANKS, J. Handbook of simulation: principles, methodology, advances, applications, and Practice. New York: John Wiley & Sons, 1998.
CHWIF, L.; MEDINA, A. C. Modelagem e simulação de eventos discretos, teoria & aplicações. São Paulo: Brazilian Books, 2007.
DETTMER, H. W. Quality and the Theory of Constraints. Quality Progress, v. 28, 77-81, 1995.
FERNANDES, C. A.; SILVA, C. S.; PEREIRA, J. O. Yamaguchi, M. M. Simulação da Dinâmica Operacional de uma Linha Industrial de Abate de Suínos. Ciência e Tecnologia de Alimentos, v.26, 166-170, 2006.
FREITAS FILHO, P. J. Introdução à Modelagem e Simulação de Sistemas com Aplicações em Arena. Florianópolis: Visual Books, 2008.
GOLDRATT, E. M. Corrente crítica. São Paulo: Nobel, 1998. 260 p.
GOLDRATT, E. M; COX, Jeff. A Meta: um processo de aprimoramento contínuo. São Paulo: Nobel, 1993. 318 p.
GOLDRATT, E. M; FOX, Robert E. A Corrida pela vantagem competitiva. São Paulo: Imam, 1992.
KELTON, W. D.; SADOWSKI, R.P; SADOWSKI, D. A. Simulation with arena. New York: McGraw-Hill, 1998.
LAW, A. M.; KELTON, W. D. Simulation modeling and analysis. New York: McGraw- Hill, 2000.
MENNER, W. A. Introduction to modeling and simulation. New York: JohnsHopkins APL Technical Digest, 1995.
MONTGOMERY, D. C. Design and Analysis of Experiments. New York: Wiley, 2005.
MARROCO, J. Análise estatística de dados – com utilização do SPSS. Lisboa: Sílabo, 2003.
OLIVEIRA, A. A.; SABBANI, F. S.; OLIVEIRA, M. J. F. Gerenciamento de restrições em hospital de câncer: um processo de melhoria continua. IN: Simpósio de Excelência em Gestão e Tecnologia. Anais... AEDB, Rio de Janeiro, 2006.
PIMENTEL, G. F. Curso de estatística experimental. Piracicaba: Degaspari, 2000. 477p.
PRADO, D. Usando o ARENA em simulação. Nova Lima: INDG - Tecnologia e Serviços LTDA, 2010. 307 p.
SARGENT, R. G. Verification and validation of simulation models. In: Winter Simulation Conference, Proceedings. Anais…, IEEE, 2009.
SENAI Restaurante Self-Service. Rio de Janeiro: Senai, 2010.