1. Introdução
A preocupação com fatores climáticos e seus efeitos nas mais diversas áreas têm crescido consideravelmente. Estudos voltados a compreender seu comportamento vêm ganhado importância nos últimos anos, onde temas como aquecimento global, emissão de gases na atmosfera, índices pluviométricos, impactos da constante poluição principalmente nas grandes cidades, qualidade do ar, índices de poluentes, raios solares, efeito estufa etc., vem sendo constantemente debatidos e podem ser vistos em diversos trabalhos publicados na literatura.
Em Fortaleza, MAGALHÃES E ZANELLA (2011) buscaram entender o comportamento das variáveis climáticas: temperatura do ar e índices pluviométricos. Verificando uma tendência crescente de chuvas e um comportamento heterogêneo espacial e temporalmente, porém similar a cada ano, podendo causar chuvas excessivas em curtos períodos acarretando sérios problemas a população. O estudo da temperatura do ar apresentou pouca variabilidade temporal com 2ºC entre a temperatura máxima e mínima. Subsidiando informações necessárias para se compreender a dinâmica dos mesmos para a região.
Os impactos ambientais no ecossistema urbano foram analisados em estudo desenvolvido por MUCELIN E BELLINI (2008). Estes autores concluíram que a inadequada utilização dos ambientes urbanos nas cidades do Brasil acena para um comportamento comumente observável e implicam em danos ambientais graves e inconsequentes.
Por meio do ajuste de modelos matemáticos ESPINOSA et al. (2010) buscaram prever os focos de calor do Mato Grosso do Sul. Concluindo que previsões são importantes, pois permitem medidas preventivas para a diminuição desses números e, dessa forma, ajudam a diminuir os danos causados, não só ao meio ambiente, mas na saúde e na economia desse Estado.
Para ASSIS (2000), as cidades, devido à quantidade de energia que utilizam, constituem as maiores fontes indiretas de gases causadores do efeito estufa relacionados ao aquecimento global.
CONTI (2005) discute as principais questões climáticas que vem sendo estudadas com especial interesse aos trabalhos que se dedicam às ciências da natureza e da sociedade. Segundo o autor a questão das mudanças climática precisa passar por uma apreciação mais refinada a fins de que se possa determinar o papel da natureza e o da ação do homem no processo, mesmo porque as duas esferas podem causar influências.
CHECHI E SANCHES (2013) utilizaram a análise de séries temporais aplicada a dados climatológicos de Erechim – RS com a finalidade de modelar os índices médios mensais pluviométricos. E concluíram que as diferenças encontradas nos extremos pluviométricos estão associadas à participação do fenômeno ENOS no período estudado tanto na sua fase positiva (El Niño) como na fase negativa (La Niña). Os mesmos autores analisaram o comportamento do fenômeno ENOS no Alto Uruguai utilizando-se de dados de precipitação dos municípios do Rio Grande do Sul de Erechim, Quatro Irmãos e Erebango, demonstrando que em anos enquadrados como muito úmidos estão relacionados com fenômeno (El Niño) já nos anos considerados secos ou extremamente secos apresentam baixa correspondência com o fenômeno (La Niña).
Ainda, segundo GIODA E GIODA (2006), em grandes cidades, elevados níveis de poluição oriundos da circulação de automóveis, caminhões/ônibus, indústrias e outras fontes, associadas às constantes alterações entre níveis máximos e mínimos na temperatura e umidade relativa do ar, potencializam a concentração de poluentes causando danos à saúde, que podem variar desde mudanças bioquímicas e fisiológicas a episódios de sinusite, hipertensão, ardência nos olhos, estresse, escamação da pele, perda dos sentidos, dificuldade de respirar, tosse e agravamento de doenças respiratórias e cardíacas.
O conhecimento da umidade relativa do ar e suas interações com outros elementos meteorológicos, segundo DELGADO (2007), ajudam no planejamento, manejo e gestão dos recursos hídricos. E, a sua medição ou estimativa é fundamental em diversas áreas do conhecimento, como em estudos bioclimatológicos e agrometeorológicos.
Algumas áreas podem se beneficiar diretamente de estudos climatológicos, como o setor primário (agricultura) e a área da saúde. BARCELLOS et al. (2009) destacam que o clima da Terra esteve, desde sempre, sujeito a mudanças produzidas por ciclos longos ou curtos, que estão registrados na história da humanidade. Além disso, destacam que ainda são necessários estudos mais detalhados no nível regional para verificar o impacto destes eventos na dinâmica de doenças infecciosas.
Da mesma forma, BARCELLOS et al. (2009) recomenda que novas metodologias devem ser buscadas, o que inclui a análise de extensas séries temporais em fatores climáticos, considerando que diversas doenças, principalmente as transmitidas por vetores, são limitadas por variáveis ambientais como temperatura, umidade, padrões de uso do solo e de vegetação.
Assim, é importante testar modelos estatísticos para dados climatológicos que podem, posteriormente, ser utilizados em outras regiões apenas modificando as séries históricas.
Apesar de um número crescente de trabalhos abordando modelagens estatísticas aplicadas a séries históricas em diversas áreas, existem poucas pesquisas de séries temporais aplicadas para a varável Umidade Relativa do Ar (UR). Com isso, se destaca a contribuição deste estudo, devido à grande influência que a variável em estudo pode ter em diversas áreas (econômicas, climatologia, epidemiologia, entre outras).
Assim, o objetivo deste trabalho é realizar uma comparação entre o desempenho de duas classes de modelos utilizados para ajuste e previsão em séries temporais: modelos de alisamento exponencial Holt-Winters e modelos Autorregressivos Integrados de Médias Móveis sazonais (SARIMA) aplicados à série histórica de Umidade Relativa do Ar de Santa Maria – RS..
2. Metodologia
Os dados em análise referem-se à série histórica de 147 observações da média mensal da Umidade Relativa do Ar (UR), coletados diariamente, no período compreendido entre outubro de 2001 a janeiro de 2014 na Estação Climatológica de Santa Maria - RS (OMM: 83936), obtidos junto ao Banco de Dados Meteorológicos para Ensino e Pesquisa (BDMEP) mantido pelo Instituto Nacional de Meteorologia (INMET).
Inicialmente foram calculadas algumas medidas descritivas da variável (média, mediana, desvio-padrão, coeficiente de variação, mínimo e máximo) com o objetivo de caracterizá-la.
Posteriormente foi ajustado um modelo SARIMA à série histórica, considerando a presença da componente sazonal.
Conforme MORETTIN E TOLOI (2004), uma série temporal é qualquer conjunto de observações ordenadas no tempo. E segundo BATISTA (2009) o objetivo da análise de séries temporais é construir modelos com propósitos determinados, tais como: descrever o comportamento da série, investigar o mecanismo gerador da série, fazer previsões de valores futuros e procurar periodicidades relevantes nos dados.
Ainda de acordo com BATISTA (2009) dentre os modelos paramétricos a classe de modelos ARIMA vem sendo largamente utilizado.
O modelo proposto por BOX E JENKINS (1976) consiste em ajustar modelos ARIMA (p,d,q) a um conjunto de dados. Onde p é o número de parâmetros da parte autorregressiva (AR), d é o número de diferenças sucessivas que devem ser aplicadas à série e q é o número de parâmetros da parte de médias móveis (MA).
A construção do modelo é fundamentada em um ciclo interativo, onde a escolha da estrutura do modelo é baseada nos próprios dados.
Segundo BOX et al. (1994), para a construção do modelo são consideradas três etapas:
1) Identificação: consiste em descobrir qual dentre as várias versões dos modelos de Box-Jenkins, sejam eles sazonais ou não, descreve o comportamento da série. A identificação do modelo pode ser realizada analisando-se o comportamento das funções de autocorrelações (ACF) e das funções de autocorrelações parciais (PACF).
2) Estimação: consiste em estimar os parâmetros do modelo ajustado.
3) Verificação: consiste em avaliar se o modelo ajustado é adequado para descrever o comportamento dos dados.
Os estágios do ciclo interativo estão representados na Figura 1.
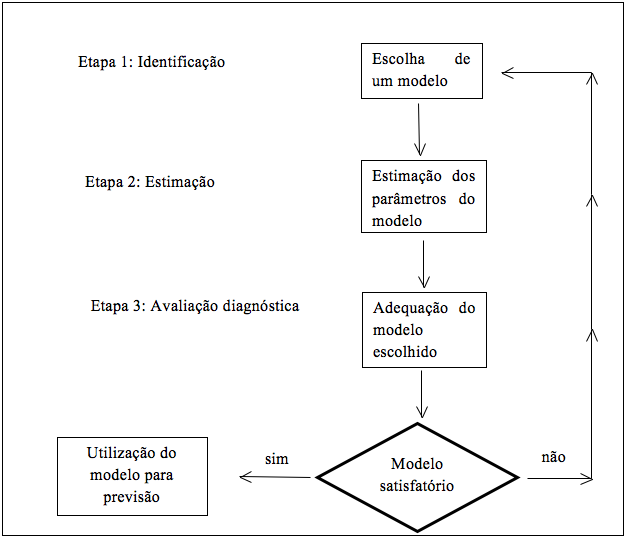
Figura 1- Fluxograma do ciclo iterativo de Box e Jenkins
Fonte: Adaptado de BOX et al. (1994).
O modelo ARIMA é um caso geral dos modelos propostos por BOX E JENKINS (1976), para o ajuste de séries temporais estacionárias. Entretanto, geralmente, as séries encontradas apresentam tendência e (ou) sazonalidade.
A não-estacionariedade de uma série implica que: a) há inclinação nos dados e eles não permanecem ao redor de uma linha horizontal ao longo do tempo e/ou b) a variação dos dados não permanece essencialmente constante sobre o tempo, isto é, as flutuações aumentam ou diminuem com o passar do tempo, indicando que a variância está se alterando, segundo WERNER E RIBEIRO (2003).
Para tornar a série estacionária, pode-se recorrer ao processo de transformações dos dados. Segundo MORETTIN E TOLOI (2004), a transformação mais comum consiste em tomar diferenças sucessivas da série original até obter uma série estacionária.
A primeira diferença de Zt é definida por:
![]()
A segunda é dada por:
![]()
Em situações normais, ainda segundo os autores citados, será suficiente tomar uma ou duas diferenças para que a série se torne estacionária. O número d de diferenças necessárias para tornar a série estacionária é denominado ordem de integração.
Assim, a inclusão do termo de ordem de integração permite que sejam utilizados a classe geral dos modelos ARIMA (p,d,q) dados pela equação:
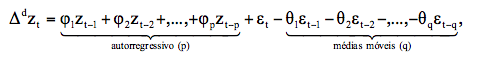
em que os parâmetros , são os parâmetros referentes à parte autorregressiva e , são os parâmetros de médias móveis, é erro que não pode ser estimado do modelo, d representa o número de diferenças aplicadas na série.
No caso em que há presença da componente sazonal nos dados, a classe de modelos é denominada SARIMA (p,d,q)(P,D,Q), dado por:
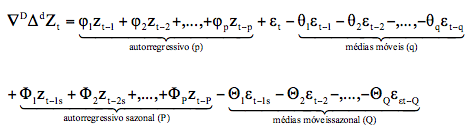
em que (P,D,Q) são referentes às ordens do modelo da parte sazonal. Os parâmetros , são os parâmetros referentes à parte autorregressiva sazonal e , são os parâmetros de médias móveis, é erro que não pode ser estimado do modelo e D indica o número de diferenças sazonais realizadas na série para estacionarizá-la.
Para um bom ajuste do modelo de Box e Jenkins, é necessário utilizar técnicas em que a estrutura residual seja um ruído branco, isto é, que o resíduo seja uma variável aleatória independente e identicamente distribuída, JUNIOR (2007).
Além disso, quando se tem por objetivo gerar previsões de valores futuros da série, os critérios ACI e BIC são utilizados para determinar a eficiência dos modelos ajustados.
Os critérios de AIC (Akaike Information Criteria) proposto por AKAIKE (1974), e o BIC (Bayesian Information Criterion) desenvolvido por AKAIKE (1978) e dados por:
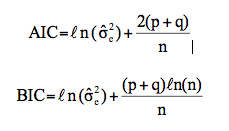
Estes critérios penalizadores levam em conta a variância do erro, o tamanho da amostra e os valores dos parâmetros estimados. Recomenda-se o ajuste de vários modelos concorrentes e, a partir dos valores dos critérios citados, escolher o modelo mais adequado para realizar previsões h-passos à frente. Quanto menores forem estes valores melhor o ajuste do modelo e, por consequência, melhores serão as previsões.
Para efeito de comparação de previsões, foi ajustado um modelo de alisamento exponencial de Holt-Winters, que pode ser de dois tipos: multiplicativo e modelo aditivo, de acordo com o comportamento das componentes da série.
Cada um dos procedimentos (aditivo ou multiplicativo) requer a determinação de três constantes de alisamento (A, C e D), associadas a cada uma das componentes para sazonalidade, nível e tendência.
Os valores das constantes (A, C e D) são obtidos de modo que se obtenha a mínima soma dos quadrados dos erros de ajustamento das constantes de suavização.
Uma das vantagens do método é a facilidade de manuseio, sendo também recomendados para séries que apresentam tendência e sazonalidade.
O modelo aditivo é apresentado pela seguinte equação:
![]()
para t=1,...,N onde N é tamanho da série.
As três equações de suavização são apresentadas abaixo:
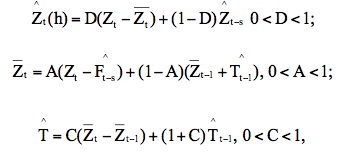
onde A, C e D são as constantes de alisamento exponencial.
A equação de previsão(h) para o modelo aditivo é dada por:
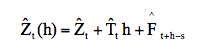
com h = 1, 2,...,s.
![]()
com h = s+1, ....,s.
O modelo multiplicativo é representado pela seguinte equação:
![]()
para t=1,...,N onde N é tamanho da série.
As três equações de suavização são apresentadas abaixo:
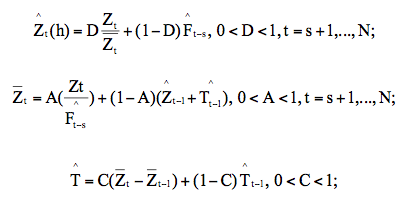
Onde: A, C e D são as constantes de suavização, que são determinados pelos vetores (A, D, C), que minimiza os erros quadráticos de previsão, s corresponde ao valor de sazonal e N o número de observações.
A equação de previsão do modelo multiplicativo é dada por:
![]()
com h = 1, 2, ......s.
![]()
com h = s+1, ......s.
Para escolha do melhor modelo serão reservadas as últimas cinco observações da série histórica para fins de comparação com os valores previstos pelos modelos ajustados, além dos critérios AIC e BIC.
Os dois critérios de avaliação da qualidade das previsões utilizados foram: MAD (mean absolute deviation) e SSE (sum of square for forecast error), apresentados a seguir:
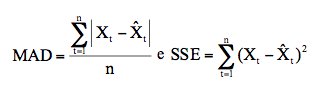
onde: é o valor da série no instante t;
é o valor previsto para o instante t;
n é o número período de tempos.
O MAD representa a diferença absoluta média entre o valor atual e o valor previsto, enquanto que o SSE é a soma dos quadrados destas diferenças.
Para o ajuste e estimação dos parâmetros dos modelos SARIMA e de Holt-Winters foi utilizado o Software livre R.
3. Resultados
Para um melhor entendimento da variável UR são apresentadas, na Tabela 1, algumas medidas descritivas.
Tabela1 - Medidas descritivas da Umidade Relativa de Santa Maria – RS, 2001 a 2014
Medida Descritiva |
Resultado |
Média |
0,77996 |
Mediana |
0,78713 |
Desvio Padrão |
0,06044 |
Coeficiente de variação |
7,75346% |
Valor máximo |
0.60882 |
Valor mínimo |
0.89675 |
Inicialmente, pode-se observar, na Figura 2, o comportamento da série original buscando identificar suas componentes, como tendência e/ou sazonalidade.
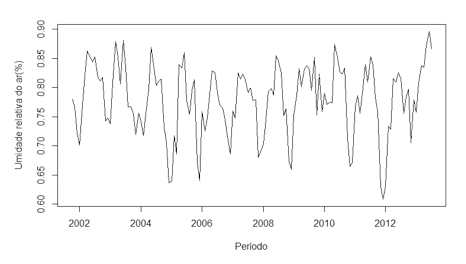
Figura 2 - Série Original da Umidade Relativa em Santa Maria - RS
Analisando-se a Figura 2, verifica-se que a série possui um padrão de sazonalidade com períodos bem definidos, não demonstrando presença de tendência, o que indica não ser necessário aplicar diferenciações na série original.
A decomposição da série original também permite identificar componentes importantes da série e confirmar se há presença de sazonalidade e/ou tendência. Considerando-se as Figuras 3a e 3b, pode observar, respectivamente, que a série não possui tendência mas que tem sazonalidade.
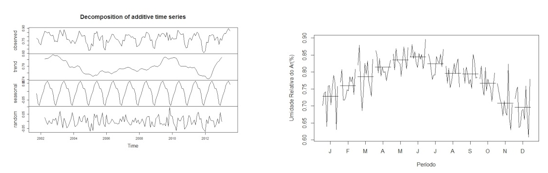
Figura 3 - (3a) Decomposição da série temporal em componentes de sazonalidade,
de tendência e de aleatoriedade, (3b) Subséries mensais de sazonalidade
As médias mensais plotadas dentro de seus meses formam as subséries (Figura 3), demonstrando a presença de sazonalidade e os períodos onde se concentram as altas e baixas (UR), demostrando haver um comportamento definido ao longo do tempo e, portanto, que podem ser ajustadas num modelo de série temporal. Além disso, observa-se que as altas concentrações de umidade ocorreram de abril a agosto, considerado período de inverno, e as mais baixas estão concentradas nos meses de dezembro e janeiro.
Após esta etapa inicial foram construídos os gráficos das funções de autocorrelação amostral (ACF) e de autocorrelação parcial amostral (PACF), que estão apresentadas na Figura 4.
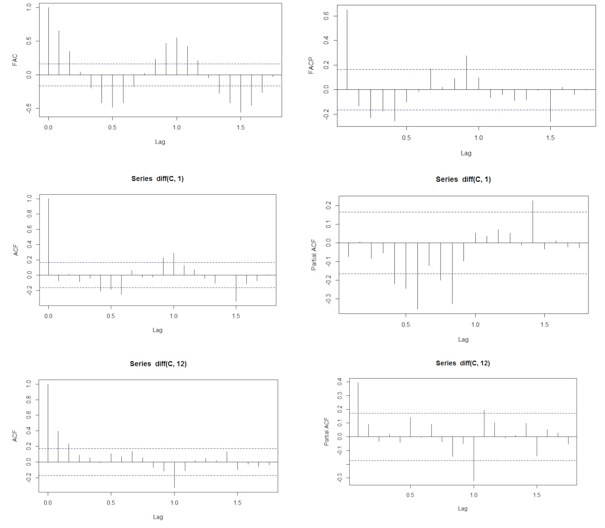
Figura 4 - Função de Autocorrelação (ACF) e Autocorrelação Parcial (PACF)
Os correlogramas apresentam as correlações seriais no domínio do tempo. Com base em suas frequências estimadas é possível verificar sazonalidades e ciclos na série. Na Figura 4 apresenta-se os correlogramas das séries, sem diferença, diferença de ordem 1 e diferença de ordem 12. Os gráficos das ACF e PACF da série em nível apresentam maior correlação do quando comparadas às ACF e PACF amostrais da série com uma diferença de ordem 1 indicando não ser necessária a aplicação desta diferença. O pico de correlação significativa na defasagem sazonal (1.0) que pode ser observada nas ACF e PACF amostrais com diferença de ordem 12 revela a presença de sazonalidade, o que indica que um modelo do tipo SARIMA deve ser considerado.
Ao se analisar os ACF e PACF com diferença de ordem 1, percebe-se características de um modelo estacionário, autorregressivo de ordem 2 e de médias móveis de ordem 1 ou 2. Essa análise é sumária para dar início ao processo de modelagem, embora vários modelos de ordem diferentes aqui serão considerados.
Na Tabela 2 estão apresentados alguns modelos concorrentes ajustados para a série UR, com os respectivos valores de AIC e BIC.
Tabela 2 - Modelos concorrentes SARIMA e os respectivos critérios
SARIMA |
AIC |
BIC |
(2,0,0 )(1,0,1 )12 |
-502,26 |
-484,52 |
(2,0,0)(2,0,0) 12 |
-485,28 |
-467,44 |
(1,0,0)(1,0,1) 12 |
-504,54 |
-489,76 |
(2,0,0)(1,0,1) 12 |
-503,91 |
-486,18 |
(1,0,0)(2,0,1) 12 |
-502,93 |
-485,20 |
(2,0,1)(2,0,1) 12 |
-501,02 |
-477,37 |
(2,0,0)(2,0,2) 12 |
-502,68 |
-481,99 |
(2,0,0)(1,0,2) 12 |
-502,45 |
-481,72 |
Os parâmetros do modelo SARIMA ajustado para a série histórica UR estão na Tabela 3, com um parâmetro autorregressivo na parte ordinal e um parâmetro autorregressivo e de médias móveis na parte sazonal.
Tabela 3 - Parâmetros do modelo selecionado
Modelo |
Parâmetros |
(1,0,0)(1,0,1)12 |
: 0,4606 |
: 0,9993 |
|
: -0,9692 |
Após selecionado o modelo SARIMA (1,0,0)(1,0,1)12, por meio dos critérios de seleção AIC e BIC, analisou-se a condição de ruído branco (média zero, variância constante, erros descorrelacionados) do modelo.
Considerando-se a análise dos resíduos observou-se que média zero e variância constante. Nos gráficos de autocorrelação dos resíduos (Figura 5), é possível perceber que não há autocorrelação significativamente diferente de zero em nenhuma defasagem, indicando que os resíduos são independentes, concluindo-se que os pressupostos de ruído branco foram atendidos.
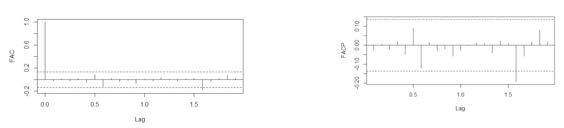
Figura 5 - Função de autocorrelação (ACF) e autocorrelação parcial dos resíduos (PACF)
Nesta etapa do trabalho foram traçadas previsões da UR para um horizonte de cinco passos à frente, ou seja, meses que não foram considerados no ajuste do modelo. Na Figura 6 é demonstrada a série ajustada e os valores previstos para os limites de previsão com intervalo de confiança de 95%.
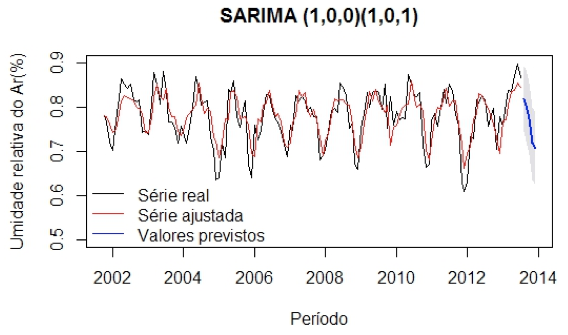
Figura 6 - Série ajustada (linha vermelha) dentro do período observado, e previsões com cinco períodos à frente (linha azul) e série observada (linha preta)
As previsões para o modelo ajustado SARIMA (1,0,0)(1,0,1)12 podem ser observadas na Tabela 4.
Tabela 4 - Valores Previstos (h=5)
Período |
Valores Previstos |
Agosto (2013) |
0,81853 |
Setembro (2013) |
0,80408 |
Outubro (2013) |
0,77372 |
Novembro (2013) |
0,71800 |
Dezembro (2013) |
0,70668 |
Considerando o modelo de alisamento exponencial de Holt-Winters, os valores das constantes de suavização que melhor se ajustaram para o modelo aditivo foram: A= 0,268; C=0,0001 e D=0,0025. E, para o multiplicativo, foram A=0,5171; C=0,0938 e D=0,0001.
Os resultados da comparação entre o modelo aditivo e multiplicativo estão na Tabela 5, além dos respectivos valores para a série real.
Tabela 5 - Valores Previstos (h=5)
Período |
Modelo Aditivo |
Modelo multiplicativo |
Série real |
Agosto |
0,84284 |
0,84781 |
0,83113 |
Setembro |
0,83348 |
0,84451 |
0,77983 |
Outubro |
0,81596 |
0,82026 |
0,73967 |
Novembro |
0,75130 |
0,75588 |
0,72708 |
Dezembro |
0,74747 |
0,74571 |
0,70064 |
Na Figura 7 podem ser observados os valores reais e previstos no caso de modelo aditivo (7a) e multiplicativo (7b).
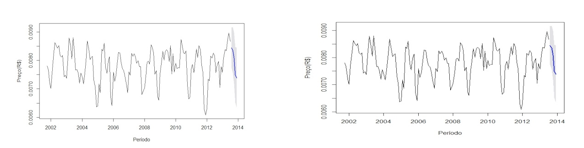
Figura 7 - (7a) Holt-Winters aditivo e (7b) Holt-Winters multiplicativo
O modelo aditivo indicou um melhor ajuste para a série histórica em análise UR conforme os critérios considerados.
Um dos objetivos de uma modelagem de séries temporais é fazer previsões de valores futuros. Para tanto, se faz necessário verificar a eficiência e o bom ajuste do modelo. Conforme proposto na metodologia foram reservados os últimos cinco valores da série original para verificar a qualidade do ajuste do modelo e comparar os modelos propostos dentro de cada classe considerada.
Tabela 6 - Resultados das previsões obtidas dos modelos ajustados (h=5)
Período |
Holt-Winters |
Modelo SARIMA (1,0,0)(1,0,1)12 |
Série real |
Agosto (2013) |
0,84284 |
0,81853 |
0,83112 |
Setembro (2013) |
0,83348 |
0,80408 |
0,77983 |
Outubro (2013) |
0,81596 |
0,77372 |
0,73967 |
Novembro (2013) |
0,75130 |
0,71800 |
0,72708 |
Dezembro (2013) |
0,74747 |
0,70668 |
0,70064 |
Considerando os critérios MAD e SSE propostos, o modelo ajustado foi um SARIMA (1,0,0)(1,0,1)12.
4. Conclusões
Ao final deste estudo observou-se que a série histórica de Umidade Relativa do Ar em Santa Maria – RS apresentou sazonalidade, com elevados valores de umidade no período de abril a agosto e, reduzidos valores, nos meses de dezembro e janeiro. Estas oscilações podem ocasionar sérios problemas respiratórios e representam um grande problema para a conservação de alimentos e sementes. Em estudos futuros pretende-se verificar a relação entre os problemas respiratórios ocasionados em períodos de altas UR.
Em relação aos modelos utilizados para comparação, observou-se que a classe SARIMA, proposta por Box e Jenkins permitiu melhor ajuste e produziu valores de previsão mais eficientes do que os modelos de Holt-Winters.
Apesar destas duas classes de modelos serem aqui utilizadas e comparadas apenas para dados de uma variável climatológica, destaca-se a ampla possibilidade de utilização destas (e de outras) técnicas adequadas a séries temporais nas mais diversas áreas em que se tem por objetivo descrever um processo temporal ou quando se deseja fazer previsões, podendo ser utilizadas como ferramenta de apoio nas tomadas de decisão.
5. Referências bibliográficas
Akaike, H. A. (1974); "A new look at the statistical model identification. IEEE Transactions on Automatic Control", v.19, n.6, p.716-723.
Akaike, H. A (1978); "Bayesian analysis of the minimum AIC procedure". Annals of the Institute of Statistical Mathematics, Tokyo, v.30, p.9- 14.
Assis, E. S. (2000); "Impactos da forma urbana na mudança climática: Método para a previsão do comportamento térmico e melhoria de desempenho do ambiente urbano". 2000, 273 f. Tese (Doutorado em Arquitetura e Urbanismo) - Universidade de São Paulo. São Paulo.
Barcellos, C., Monteiro, A. M. V., Corvalan, C., Gurgel, H. C., Carvalho, M. S., Artaxo, P., Hancon, S., Ragoni, V., (2009);. "Mudanças climáticas e ambientais e as doenças infecciosas: cenários e incertezas para o Brasil". Epidemiologia e Serviços de Saúde 18 (3), p.285-304.
Batista, A. L. F. (2009); "Modelos de séries temporais e redes neurais na previsão de vazão", 2009, 79 f. Dissertação de Mestrado (Mestrado em Engenharia de Sistemas) – Universidade Federal de Lavras, Lavras.
Box, G. P.; Jenkins, G. M. (1976); Time series analysis, forecasting and control; San Francisco, Ed. Holden-Day.
Box, G. E. P.; Jenkins, G. M.; Reinsel, G. C. (1994); Time Séries Analysis: Forecasting and Control. New Jersey, Prentice Hall, 548p.
Chechi, L.; Sanches, F. O. (2013); "O Uso do Índice de Anomalia de Chuva (IAC) na avaliação do Fenômeno do El Niño Oscilação Sul (ENOS) no Alto Uruguai Gaúcho entre 1957-2012". Revista de Geografia e Física,v. 06 p. 1586-1597.
Chechi, L.; Sanches, F. O. (2013); "Análise de uma série temporal de precipitação para
Erechim (RS) e um possível método de previsão climática". Revista Ambiência Guarapuava, v.9, p. 43-45.
Conti, J. B. (2005); "Considerações Sobre as Mudanças Climáticas Globais". Revista do Departamento de Geografia (USP), p. 82-88.
Delgado C.R, Gilberto Chohaku Sediyama G.C, Andrade R.G, Menezes S.J.M.C, (2007); "Modelos para prognósticos da umidade relativa do ar em escala horária no município de Muriaé, MG", I Seminário de Recursos Hídricos da Bacia Hidrográfica do Paraíba do Sul: o Eucalipto e o Ciclo Hidrológico, Taubaté, Brasil, IPABHi, p. 295-300.
Espinosa, M. M.; Prado, S. M.; Ghelerre, M. (2010); "Uso de modelo SARIMA na previsão de focos de calor para os meses de junho a outubro no Estado do Mato Grosso". Revista Ciência em Natura, 32(2), p 7-21.
Gioda, A.; Gioda, F. R. (2006); "A influência da qualidade do ar nas doenças respiratórias". Revista Ambiente e Saúde, v7(1), p. 15-23.
Instituto Nacional de Meteorologia (INMET). Acesso em 10 de fevereiro de 2014. Disponível em: htp://www.inmet.gov.br/.
JUNIOR, A. M. (2007); "Análise de métodos de previsão de demanda baseados em séries temporais em uma empresa do setor de perfumes e cosméticos", 2007, 100 f. Dissertação de Mestrado (Mestrado em Engenharia de Produção) – Pontifícia Universidade do Paraná, Curitiba.
Magalhães, B. G.; Zanella M. E. (2011); "Comportamento Climático da região Metropolitana de Fortaleza". Revista Mercator, V10, p 129-145.
Morettin, P. A.; Toloi, C. M. C. (2004); Análise de Séries Temporais. São Paulo: Edgard Blucher LTDA, 535 p.
Mucelin, C. A.; Bellini, M. (2008); "Lixo e Impactos Ambientais Perspectivas no Ecossistema Urbano". Revista Sociedade & Natura, 20(1), p. 111-124.
Werner, L.; Ribeiro, J. L. D. (2003); "Previsão de Demanda: Uma Aplicação dos Modelos Box Jenkins na Área de Assistência Técnica de Computadores Pessoais". Revista Gestão & Produção,v10, n1, p.47-67.