1. Introdução
A ovinocultura no Rio Grande do Sul teve papel fundamental no progresso da pecuária gaúcha. Durante o século XX a atividade evoluiu promovendo desenvolvimento econômico e social e posicionando o estado como um dos maiores produtores do país. No entanto, ao longo das últimas três décadas a atividade foi marcada por períodos de fortes oscilações na produção de lã e carne ovina.
A crise internacional da lã causou redução drástica no rebanho, comprometendo sobremaneira a estrutura da oferta de carne e lã. Os rebanhos de raças laneiras foram os mais atingidos e acabaram dando espaço para a entrada de raças especializadas em carne.
O período de crise na atividade surgiu no final da década de 1980, em consequência dos altos estoques australianos de lã e do início da comercialização de tecidos sintéticos no mercado têxtil internacional. A crise que se estendeu durante a década de 1990, desestimulou a atividade e desestruturou toda a cadeia produtiva da ovinocultura, reduzindo significantemente o rebanho comercial. Com esse cenário, os ovinos deslanados surgiram como alternativa viável e permitiram o desenvolvimento da ovinocultura em regiões que, até então, não tinha expressão econômica, como por exemplo, o nordeste brasileiro.
Segundo Viana (2008) o aumento do poder aquisitivo da população, a estabilidade monetária conquistada a partir do Plano Real, a abertura da economia brasileira à competitividade internacional e o incremento do abate de animais jovens trouxeram um novo mercado para a ovinocultura. A carne ovina começou a ser apreciada, levando ao incremento de demanda. Esse novo cenário possibilitou o início da reestruturação da ovinocultura no Rio Grande do Sul, com a transição do sistema produtivo laneiro para o sistema de produção de cordeiros para abate. Dessa forma, a carne tornou-se o principal produto da ovinocultura.
Apesar de existir um potencial mercado para a ovinocultura no Brasil. A inexistência de um mercado fiel, a exigência de uma oferta regular de animais, a necessidade de escala para comercialização e a busca por animais jovens por parte dos frigoríficos são dificuldades enfrentadas pelo segmento de carne ovina no Brasil.
Em consequência, ganham espaço no mercado interno gaúcho as importações de carne ovina, apresentadas como uma ferramenta para irrigar esse deficitário mercado e, assim, possibilitar aos consumidores uma carne com um preço mais acessível economicamente.
Nos últimos dez anos, não menos de 50% do total consumido de carne ovina no Brasil foi importado. O Uruguai é o principal parceiro comercial do país na importação de carne ovina, além de ser o maior player das Américas no agronegócio da carne ovina. No período de 2002 a 2009 o Brasil importou do país vizinho algo em torno de 90% do total das importações de carne ovina anual realizada.
Considerando a importância e o potencial da cadeia produtiva ovina para o Brasil e, em especial para o Rio Grande do Sul, e os seus dois principais parceiros comerciais, o Uruguai e a Austrália, espera-se que as oscilações de preços da carne ovina e da lã, respectivamente, desses países afetem a dinâmica do mercado brasileiro desses produtos.
Os trabalhos empíricos realizados na tentativa de averiguar se há transmissão de preços em determinados mercados, ou seja, se estes são espacialmente integrados, caracterizam que a integração de mercado é um processo pelo qual preços de commodities idênticas não se comportam de forma independente. Nesse sentido, integração espacial de mercados se refere à medida do grau de integração de mercados, ou seja, por um lado, existem mercados completamente isolados e, por outro, aqueles perfeitamente integrados, sendo importante na medida em que pode ocorrer transmissão de preços indiretamente, ou seja, não é necessário que duas regiões sejam parceiras diretas de comércio para existir alto grau de integração entre elas.
Quando os preços são determinados de maneira interdependente no sentido de que as alterações de preços em um mercado são transmitidas aos preços em outros mercados, tem-se caracterizado os chamados mercados integrados, o qual tem como fundamento teórico a Lei do Preço Único (LPU).
Diante do que foi relatado acima, pode-se encerrar a problemática com o seguinte questionamento: ocorre transmissão de preços entre os mercados de carne ovina e da lã entre o Rio Grande do sul, Uruguai, Brasil e Austrália? De maneira específica, o presente estudo questiona se as oscilações nos preços da carne ovina uruguaia, na lã brasileira e na lã australiana irão repercutir nos preços internos recebidos pelos produtores do Rio Grande do Sul, e qual é a velocidade de transmissão entre estes preços?
Para responder a essa problemática, o presente trabalho tem como objetivo precípuo verificar se há integração entre os preços da carne ovina no Rio Grande do Sul, no Uruguai, da lã no Brasil e da lã na Austrália buscando, assim, identificar um comportamento comum de longo prazo.
2. Referencial teórico
O referencial teórico utilizado neste estudo teve como base a teoria de integração de mercados, na forma como foi apresentada em Fackler e Goodwin (2000) e González-Rivera e Helfand (2001), e a Lei de Preço Único.
Segundo Fackler e Goodwin (2000), a integração de mercados refere-se à interdependência entre os preços em diferentes regiões, ao longo do tempo. Por compartilharem informações de longo prazo semelhantes, os preços de um mercado integrado sofrerão influência não apenas das condições de oferta e demandas locais, mas também das condições das demais localidades. Neste sentido, os testes estatísticos são empregados para indicar o grau de integração dos mercados.
Para Barrett (2001), se dois mercados estão integrados, então, choques de preço em um deles devem ser sentidos em outros mercados para o mesmo bem. Entretanto, Faminow e Benson (1990), salientam que a arbitragem garante que os preços em locais espacialmente diferentes não diferirão mais do que o custo do transporte de enviar o produto de um lugar para outro.
A base da análise da integração dos mercados encontra-se na LPU, garantida pela arbitragem dos mercadores. Por isso, a LPU é uma relação que se cumpre no longo prazo, sem excluir a possibilidade de desajustes de preços no curto prazo (COSTA e FERREIRA FILHO, 2000).
Arbitragem espacial, “Lei do Preço Único” e integração espacial de mercados são termos que se confundem e se inter-relacionam. No entanto, o que diferencia integração espacial de mercados dos demais termos é que este se refere à medida do grau de integração de mercados, ou seja, por um lado, existem mercados completamente isolados e, por outro, aqueles perfeitamente integrados (em que a LPU é observada). De forma sucinta, integração espacial de mercado diz respeito ao grau de co-movimentação dos preços em diferentes locais, sendo medido pela correlação entre os preços (FACKLER e GOODWIN, 2000).
Fackler e Goodwin (2001 apud CUNHA, 2008) definem três diferentes versões para a LPU. A primeira é conhecida como versão fraca dessa Lei e estabelece que a diferença entre os preços e um bem em dois locais deve ser menor ou igual ao custo de mover este bem da região com menor preço para a região com preço maior. A versão forte da LPU estabelece que esta condição conhecida como condição de arbitragem espacial, deve se manter como uma igualdade. Embora, este seja um conceito de equilíbrio, os preços podem diferir desta relação, mas a ação de arbitragem levará a diferença de preços a se igualar ao valor dos custos de transação. A terceira e última está relacionada à versão agregada ou Paridade do Poder de Compra definida em termos de índices de preços, indica que a taxa de troca entre bens comercializáveis é proporcional à relação dos níveis de preços em dois países.
A validade da Lei do Preço Único está diretamente relacionada ao processo de arbitragem internacional, o qual, no longo prazo, tende a igualar os preços nos dois mercados (doméstico e externo). A arbitragem induz a elevação do preço no país com preço baixo, em função do aumento da quantidade demandada, enquanto implica em queda de preço no país com preço alto, devido ao excesso da quantidade ofertada. O processo de arbitragem continua até o momento em que os preços nos dois países sejam igualados. No entanto, Cunha (2008) alerta para o fato de que o processo de arbitragem poderá ser dificilmente eficiente em razão de barreiras comerciais, informação imperfeita e aversão ao risco. Além disso, o autor destaca que a maioria das firmas possui algum poder de mercado já que em grande parte dos mercados a pressuposição de competição perfeita não se verifica. Para Nogueira et. al (2005), o processo de arbitragem leva algum tempo para se efetivar em decorrência de sua ação lenta o que conota no curto prazo a ineficiência da LPU. De acordo com Kimura (2003) também existe uma limitação da arbitragem no mercado financeiro, uma vez que as possibilidades de arbitragem não são totalmente eliminadas devido à estrutura do mercado e então prováveis distúrbios no mercado podem causar desequilíbrios persistentes de preço.
3. Metodologia
3.1 Fonte e base de dados
Os dados utilizados no estudo são as séries mensais de preços da carne ovina do Rio Grande do Sul (PCRS) e do Uruguai (PCUR) e as séries de preço da lã do Brasil (PLBR) e da Austrália (PLA), todas no período de janeiro de 2002 a julho de 2009. As séries históricas de preço do Rio Grande do Sul foram obtidas na EMATER/RS – via sistema interno de dados – e as do Uruguai foram obtidos no Instituto Nacional de Carnes do Uruguai (INAC). As séries de preços mensais da lã do Brasil foram obtidas na FGVDADOS e da lã para a Austrália no Index Mundi. O software utilizado para estimar o modelo foi o Microfit 4.0.
3.2 O modelo econométrico
O modelo teórico a ser utilizado neste trabalho mostra como variações nos preços externos refletem-se em variações nos preços internos. Tendo como base a LPU pode-se escrever o preço interno do produto analisado como função do preço externo da seguinte forma:
em que, Pi é o preço interno do produto i no país x no período t e refere-se ao preço do produto i no período t nas regiões y, os coeficientes α e β’s, são o intercepto da função e as elasticidades dos preços internos em relação ao preço externo, respectivamente; u é o vetor de resíduo. Assim,
Pcrs : representa o preço da carne ovina no Rio Grande do Sul;
Pcur : representa o preço da carne ovina no Rio Grande do Sul;
Plbr : representa o preço da lã no Brasil
Pla : representa o preço da lã na Austrália
Este modelo parte do pressuposto que o preço do produto em determinado país é função do preço do mesmo produto em outra região e do termo de erro.
O coeficiente de inclinação é a elasticidade de transmissão de preço. Quando o seu valor é igual a 1 significa que variações no preço externo são plenamente transmitidas ao preço doméstico; por outro lado, quando o valor de β é igual a zero isso implica que variações do preço externo não conduzem a qualquer tipo de resposta do preço interno. Nesse caso, portanto, considera-se que o mercado analisado seja fechado. O caso mais comum é que o valor de β se encontre entre 0 e 1, mostrando que as inter-relações comerciais dos países afetam de alguma forma os preços dos produtos comercializados por eles.
Espera-se a priori que os preços da carne ovina no Uruguai e da lã na Austrália afetem de forma negativa e positiva, respectivamente, os preços da carne ovina no Rio Grande do Sul e de certa forma, que aumentos de preços nestes produtos sejam transmitidos ao mercado interno considerando as peculiaridades do mercado de carne ovina.
3.3 Procedimentos Econométricos
No estudo serão realizados os testes de estacionariedade através dos procedimentos clássicos, como a função de autocorrelação (FAC) e os Testes de DF, DFA e PP, bem como, o teste de causalidade de Granger e o teste de co-integração de Johansen, a decomposição da variância, o mecanismo de correção dos erros e, de forma complementar, as estimativas da função impulso-resposta e do perfil de persistências. A seguir são detalhados os dois últimos procedimentos, para os demais ver Gujarati (2006), Coelho (2002), Enders (1995), Rosado (2006), Araújo Filho (2005), Cunha (2008), entre outros autores que abordam procedimentos econométricos.
3.3.1 Função impulso-resposta e perfil de persistência
A função impulso-resposta (FIR) é uma técnica que permite avaliar os efeitos de um choque numa série temporal sobre a outra. Conforme Fackler e Goodwin (2001 apud CUNHA, 2008) é um método utilizado para medir o grau de integração de um mercado, assim, a FIR mede a resposta das variáveis incluídas num VAR a choques exógenos sobre uma das variáveis do modelo, ao longo do tempo. Essa metodologia é usada nos estudos de integração de mercados para avaliar a dinâmica do ajustamento entre os preços, pois este procedimento permite traçar os efeitos do desvio padrão de um choque relativo a uma inovação nos valores presentes e futuros das variáveis endógenas. Esse fato é transmitido por uma estrutura dinâmica de um vetor auto-regressivo.
A metodologia de cálculo dos perfis de persistência, foi inicialmente sugerida por Pesaran e Shin (1996) e empregada por González-Rivera e Helfand (2001), Pereira (2005) e Nogueira et al. (2005). Os perfis de persistência visam sintetizar as estimativas dos parâmetros do VEC em uma medida única, que defina o grau de integração; servem para qualquer ordenamento das variáveis no sistema; e caracteriza a resposta de uma relação co-integrante a um choque em um sistema amplo, ao invés de um sistema individual. Ele mede o tempo de reação de cada relação de equilíbrio de longo prazo para absorver um choque em um sistema amplo.
4. Análise de resultados
A análise de séries temporais requer que se adotem alguns procedimentos padrões, como os tratados na seção anterior. O primeiro passo nessas análises é verificar a presença de raiz unitária, e para tal finalidade o presente estudo recorre-se aos testes do correlograma, DF e ADF e Phillips-Perron (PP).
Os correlogramas das séries estudadas revelam que os coeficientes de autocorrelação iniciam com valores altos e decaem lentamente com o aumento do número de defasagens, caracterizando um padrão típico de passeio aleatório.
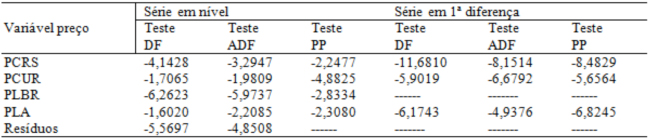
Uma vez detectado indícios de que as séries parecem ser não estacionárias, passa-se a realizar testes mais formais como o Teste ADF e PP, o qual pode ser observado na Tabela 1. As séries em estudos mostram-se influenciadas pela tendência, no caso da carne ovina Uruguaia e lã Brasil e sem tendência, no caso das demais.
Fonte: dados da pesquisa
Notas: Estatísticas críticas de DF = -2,89, para 95% de confiança, ADF = - 3,45.
Como verificado pelos correlogramas, as séries apresentam um padrão de autocorrelação, isto é, as séries temporais em estudo são não estacionárias. Assim, utilizam-se as estatíticas DFA, que contemplam a presença da autocorrelação no processo em questão. Assim, a partir dos valores dos Testes ADF se verifica que os processos PCRS, PCUR e PLA são, em termos estatísticos, não estacionárias em nível, a 5% de significância. E que a série PLBR é estacionária ao nível de 5% de significância, sendo, portanto, integrada de ordem zero – I(0). O teste Phillips-Perron mostrou-se contraditório com algumas estatísticas apontadas pelo teste ADF. O teste PP apontou como estacionária em nível a variável PCUR e, não estacionária em nível a variável PLBR contradizendo, assim, as estatísticas ADF discutidas acima. Deste modo, este estudo desconsidera tal contradição, a fim de não perder informações anteriores e, ainda, observa-se que há indícios de não estacionariedade, no caso de PCUR e, estacionariedade, no caso de PLBR, como já revelado pelos correlogramas e ratificado pelo teste ADF.
Em relação ao vetor de resíduos a série é estacionária em nível sendo, portanto I(0). Nesse caso, o teste apropriado para o termo de erro é DF, dada à pressuposição de que esta variável não apresenta autocorrelação. Dessa forma, já se têm o primeiro indício de que as variáveis em estudo guardam relação de equilíbrio de longo prazo. Destaca-se que o vetor de resíduos não se apresenta influenciado pela tendência.
Um novo padrão de estacionariedade pode ser observado nos correlogramas obtidos a partir da primeira diferença das séries PCRS, PCUR e PLA, os coeficientes de autocorrelação diminuem acentuadamente após uma defasagem, oscilando em torno de zero, sugerindo a ausência de raiz unitária. Tal padrão é confirmado pelos testes DF em primeira diferença da Tabela 1, na qual ao nível de significância de 95%, os valores calculados das estatísticas de DF são superiores ao valor crítico. Deste modo, se aceita a hipótese de que todas as séries são estacionarias após a diferenciação, ou seja, as séries são integradas de ordem um – I(1).
Após concluir que os mercados são integrados, passou-se ao teste para verificar a causalidade no sentido de Granger entre os preços nos mercados em estudo, que foi executado com 1 defasagem segundo o critério AIC e SBC. Os resultados do Teste de Causalidade de Granger são apresentados na Tabela 2.

Fonte: dados da pesquisa. Valor crítico: 7,815. Lags: 3
Os resultados expostos na Tabela 2 confirmam em parte as expectativas. Dada a hipótese nula (H.N) de que PCUR e PLA causam, individualmente, no sentido de Granger a variável PCRS, verifica-se que os valores calculados das variáveis são maiores que os valores tabelados, logo, infere-se que as variáveis citadas são Granger-Causal. Fato este esperado, pois, no caso da carne uruguaia se confirma a teoria de que no comércio internacional desse produto os preços praticados em um país são influenciados por preços praticados em outros países que comercializam entre si. Já no caso da lã australiana, a mesma ser Granger causa preços carne ovina Rio Grande do Sul está em conformidade com as características do mercado de carne ovina gaúcha e mundial, uma vez que, com a crise internacional da lã no fim da década de 80, desencadeada nos principais mercados produtores, entre eles a Austrália, o rebanho de ovinos foi drasticamente reduzido e sua recuperação está condicionada a adoção de raças produtoras de carne e lã.
No entanto, a variável preço lã para o Brasil não causa no sentido de Granger os preços da carne ovina no Rio Grande do Sul, fato que gerou surpresa. No entanto, em situação semelhante vivenciada por Araújo Filho (2005), o autor coloca que o teste de Granger é sensível a escolha do tamanho da defasagem – a variável em estudo só se mostrou significativa com 8 defasagens – e que a causalidade de Granger tem sido utilizada nas análises de integração de mercado como uma ferramenta auxiliar, em associação com os modelos de co-integração, pois, embora o teste, num contexto de integração de mercados, permita algumas inferências sobre relações de preços regionais, ele é bastante limitado. Por indicar apenas se o relacionamento entre preços defasados e contemporâneos é estatisticamente diferente de zero, nada pode ser dito a respeito natureza real das relações; uma causalidade estatisticamente significativa pode ser totalmente inconsistente com as noções convencionais de integração. Por estes motivos optou-se por permanecer com a variável preço lã em nível de Brasil no modelo.
A fim de verificar se os preços possuem tendência semelhante de comportamento, é realizado o teste de co-integração das séries de preços estudadas através do método proposto por Johansen, porém, antes de realizar o teste de co-integração, é necessário determinar o número de defasagens a serem utilizadas – ordem do vetor autoregressivo. A ordem é determinada de acordo com os critérios de seleção de AIC e SBC. De acordo com a Tabela 3, ambos os critérios AIC E SBC apresentaram maior valor das estatísticas para defasagem de ordem um. Assim, adota-se um VAR = 1.
Tabela 3– Critérios de seleção para a escolha da ordem de defasagem do modelo

Fonte: dados da pesquisa
A definição do número de vetores co-integrados se dá pela escolha do rank da matriz (r) com base nos autovalores e no traço da matriz estocástica. Para o presente trabalho foi escolhido, como modelo representativo, aquele sem intercepto ou tendência temporal utilizado por Lopes (2008) e Araújo Filho (2005), as demais especificações foram testadas, mas não apresentaram mudanças estatísticas significativas nos ajustamentos dos processos. A Tabela 4 mostra o Teste de Co-integração de Johansen, levando-se em consideração os critérios de máximo autovalor e traço na qual se testa a existência de (k – 1) vetores de co-integração, considerando a totalidade das séries.
Tabela 4 – Teste de co-integração de Johansen

Nota: Teste de co-integração sem intercepto e sem tendência, com ordem VAR = 1. Fonte:dados da pesquisa
Conforme a tabela acima, o número de vetores de co-integração foi testado sequencialmente. Sob hipótese nula (H.N) da não existência de posto co-integrante contra a hipótese alternativa (H.A) de existir um posto, testa-se ao nível de significância de 95% e 90%, o valor crítico calculado contra os tabelados, usando a estatística do máximo autovalor. A partir disso, percebe-se a aceitação da hipótese alternativa para ambos os casos, uma vez que as estatísticas calculadas (τmax e τtrace) foram maiores que os valores tabelados. Assim, parte-se para a verificação da segunda hipótese alternativa (r = 2). Sob a mesma argumentação anterior, chega-se a conclusão, a partir dos Testes de Autovalor e do Traço, de que esta hipótese não deve ser rejeitada.
Assim, tanto o teste traço quanto o de máximo autovalor, indicaram a existência de dois vetores de co-integração estatisticamente diferente de zero, logo, há dois vetores de co-integração para as quatro variáveis em estudo, o que significa a existência de um vetor de co-integração para cada subconjunto de três variáveis e que qualquer combinação linear destes dois vetores é também um vetor de co-integração. No entanto, optou-se por utilizar somente um dos vetores, uma vez que, a normalização do PCRS já consegue atender aos objetivos do presente trabalho. E, em um segundo momento, o uso de dois vetores gerou um problema técnico, de modo que, a restrição de uma variável enfraqueceria um dos vetores.
O fato de terem sido obtidos dois vetores de co-integração não é condição suficiente para garantir a participação de cada um dos preços no equilíbrio de longo prazo do mercado de carne ovina do Rio Grande do Sul. Por esse motivo, foram testadas as hipóteses de que o parâmetro β seja estatisticamente significativo. Dessa maneira, a análise do padrão de interdependência entre os processos é a seguinte:
Tabela 5 – Resultados da estimação da regressão

Notas: Estatística t0,05 = 1,98; t0,10 = 1,65.Fonte: dados da pesquisa
Como colocado na tabela acima, o teste t para os parâmetros, ao nível de significância de 5%, indica que a variável preço da carne ovina do Uruguai é estatisticamente significativa na estimação da equação. No entanto, com um nível de 10% de significância a variável preço da lã australiana, também, se mostra significativa, indicando que ambas participam efetivamente do equilíbrio de longo prazo do mercado de carne ovina no Rio Grande do Sul.
Os resultados apontam que no longo prazo, os preços da carne ovina uruguaia têm relação negativa com os preços da carne ovina no Rio Grande do sul, de modo que, uma elevação de 1% no preço da carne ovina uruguaia ocasionaria redução em torno de 0,60% nos preços da carne ovina no Rio Grande do Sul, resultado coerente com Silva (2002). Segundo esse autor, no Rio Grande do Sul os preços pagos aos produtores uruguaios fazem uma pressão para baixo na remuneração dos produtores gaúchos.
Já o preço da lã australiana apresenta uma relação positiva. Assim, é plausível esperar que um aumento de preço da lã na Austrália influencie, diretamente, o nível de preços da carne ovina no Rio Grande do Sul. Infere-se com 90% de confiança que uma elevação de 1% no preço da lã australiana incrementaria o preço da carne ovina no Rio Grande do Sul em 0,12%. Resultados que tornam compreensíveis os efeitos da crise internacional da lã e ratificam o desenvolvimento de estratégias e políticas para a valorização da lã que conseguintemente possa levar a um incremento positivo na carne.
Assim, todos os mercados enumerados acima são relevantes no estabelecimento do padrão de equilíbrio de longo prazo no mercado de carne ovina no Rio Grande do Sul indicando que choques ocorridos em um mercado são transmitidos aos outros no longo prazo. Em outras palavras, o mercado não é segmentado e é eficiente na difusão de informações, contribuindo para o estabelecimento do padrão de equilíbrio de longo prazo no mercado em estudo.
Uma vez identificada à integração entre os preços, procurou-se determinar em quanto tempo as relações estabelecidas retornariam ao equilíbrio após uma alteração qualquer no mercado por meios dos perfis de persistência e da função impulso-resposta ortogonalizada do choque de uma unidade de desvio padrão do preço da carne ovina no Rio Grande do Sul.
Tomando-se por base a função impulso-resposta, tem-se que os efeitos provocados por choques externos à variável preço da carne ovina para o Rio Grande do Sul se propagam ao longo dos meses, dissipando-se em torno do 13° mês. É possível analisar que o preço da carne ovina para o Rio Grande do Sul, por exemplo, decorrente de um impulso dos preços de R$ 0,007 kg no Uruguai é reequilibrado no primeiro mês mediante um preço de R$ 0,03 kg. No segundo mês, o impacto residual é de R$ 0,02 e, assim até que o valor residual total seja eliminado por volta do 13º mês.
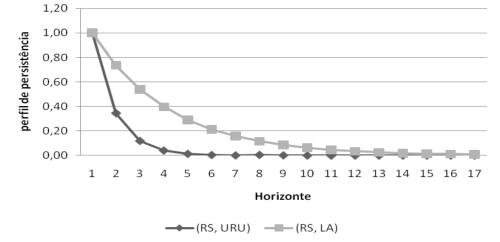
Para os perfis de persistência, os cálculos foram realizados para cada par de preços, tendo como base os preços da carne ovina para o Rio Grande do Sul. Em geral os resultados obtidos indicaram que os choques no sistema são removidos de modo relativamente rápido. Pode-se verificar que o preço da carne ovina para o Uruguai foi o que retornou ao equilíbrio mais rapidamente, com 96% dos ajustamentos ocorrendo no terceiro mês após o choque. O preço da lã australiana apresentou ajuste mais lento, cerca de 92% no oitavo mês. A Figura 1 exibe o gráfico dos perfis de persistência, indicando que, por volta de 13 meses após o choque, os pares de preços praticamente retornam ao equilíbrio.
Com o objetivo de resumir os ajustamentos discutidos numa medida que representasse o grau de integração entre os mercados, foi calculado o perfil de persistência mediano (ou meia-vida)3, definido como o tempo necessário para que ocorram 50% dos ajustes entre cada preço e aquele que foi tomado como base. Na Tabela 6 encontram-se as estimativas.
Fonte: Dados da pesquisa
A carne ovina uruguaia foi a mais integrada do mercado, pois, a qualquer choque, verifica-se uma reação de forma mais rápida, dado que sua vida média é inferior a um mês (0,87), ou seja, para esta variável 50% dos ajustamentos ocorreram até o vigésimo sexto dia posterior ao choque no sistema como um todo, no período analisado.
Em geral, o grau de integração esteve relacionado com a expressividade de cada mercado com o mercado de carne ovina no Rio Grande do Sul, como é o caso da menor integração da lã australiana. Esta também é a explicação para a maior integração da carne uruguaia.
A decomposição da variância, em termos percentuais, dos erros de previsão mostra a evolução do comportamento dinâmico apresentado pelas variáveis, ao longo do tempo, isto é, permitem separar a variância dos erros de previsão para cada variável em componentes que podem ser atribuídos por ela própria e pelas demais variáveis endógenas, isoladamente. Assim, qual o efeito que um choque não antecipado sobre determinada variável tem sobre ela própria e as demais variáveis pertencentes ao vetor co-integrável.
Os resultados da decomposição da variância dos erros de previsão para o preço da carne ovina no Rio Grande do Sul estão descritos na Tabela 7. Observa-se que, decorridos 13 meses, após um choque não antecipado sobre essa variável, aproximadamente, 56,5% de seu comportamento decorre dela própria, isto é, a variância dos erros de previsão sendo atribuídas à própria dinâmica do mercado de carne ovina do Rio Grande do Sul. O restante é atribuído, principalmente, à variável preço carne ovina no Uruguai (PCUR), participando com 42% na decomposição da variância. O mercado de lã australiano contribuiu com 1,1% no 13º período. Portanto, verifica-se que os erros de previsão são explicados em grande maioria pela própria variável PCRS.

Fonte: dados da pesquisa
As relações de longo prazo estabelecidas entre os preços são asseguradas por um mecanismo de correção de erros que as conduz ao equilíbrio. Assim, o termo de erro liga o comportamento da variável em curto prazo ao seu valor em longo prazo e, com isso, o mecanismo de correção de erros passa a evidenciar o quanto da trajetória de longo prazo da série em questão é corrigido a cada mês.
Tabela 8 – Modelo vetorial de correção de erros.

Notas: estatística t0,05 = 1,98; t0,10 = 1,65. Rio Grande do Sul como variável explicada. Fonte: dados da pesquisa
É possível verificar que o vetor de erro, em um intervalo de 95% de confiança, é significativo e apresenta-se negativo, como esperado. Isso significa que os preços da carne ovina no Rio Grande do Sul estão acima do equilíbrio no curto prazo entre os períodos t e t-1. O coeficiente obtido demonstra que a discrepância de 33,14% entre os preços da carne ovina no Rio Grande do Sul e nos outros mercados integrados está sendo corrigida a cada mês. No caso do preço da lã brasileira, os resultados apontaram coeficiente positivo e significativo, o que indica que responde aos choques de preços no curto prazo, apesar de não participar do equilíbrio de longo prazo.
Deve-se ressaltar que a integração identificada permite afirmar apenas que os preços possuem trajetórias temporais semelhantes e convergem para um equilíbrio no longo prazo, porém mantendo-se em magnitudes distintas.
5. Conclusão
Em razão da importância do setor ovinocultor no contexto socioeconômico do Rio Grande do Sul, do papel desempenhado pela integração de mercado no crescimento econômico, e considerando que nenhum estudo para o setor tinha sido realizado com o intuito de analisar a integração deste mercado, faz-se relevante saber como os vários mercados se relacionam.
A partir do procedimento de Johansen foi detectada a presença de dois vetores de co-integração, optando-se, no entanto, por utilizar somente um dos vetores, uma vez que, o mesmo atendia aos propósitos delineados pela presente pesquisa. Os resultados demonstram a existência de relações de equilíbrio de longo prazo entre os preços da carne ovina do Rio Grande do Sul e Uruguai e, da lã australiana, ou seja, tais mercados são integrados. No entanto, os preços da lã no mercado brasileiro não se apresentam estatisticamente integrada no longo tempo, participando do equilíbrio no curto prazo.
A função impulso-resposta e os perfis de persistência demonstraram que após um choque de preços os desequilíbrios são corrigidos lentamente. A decomposição da variância dos erros indica que os erros de previsão são explicados significativamente pelos preços da carne ovina no estado, ou seja, a própria variável se explica. Quanto à análise do grau de integração, ou seja, a verificação das variáveis que são mais ou menos integradas constatou-se que o Uruguai foi o que se ajustou mais rapidamente a desequilíbrios no sistema, possuindo, portanto, o maior grau de integração. Numa clara indicação de que, quanto maior a participação na produção e exportação, mais alto é o grau de integração. No que se refere às relações de curto prazo, o vetor de erro é significativo e positivo.
Conclui-se, portanto, que no período analisado houve um fluxo comum de informação ao longo dos expressivos players do setor.
Referência bibliográfica
ARAÚJO FILHO, O. DE A. (2005); Co-integração e causalidade na política de garantia de preços mínimos e preços agrícolas: o caso do milho no Brasil. Fortaleza, Dissertação (Mestrado em Economia Rural), UFC.
BARBOSA, M. Z.; MARGARIDO, M. A.; NOGUEIRA JÚNIOR, S. (2002); “Análise da elasticidade de transmissão de preços no mercado brasileiro de algodão”. Nova Economia. Belo Horizonte, v.12, n.2, jul./dez.
BARRETT, C.B. Measuring integration and efficiency in international agricultural markets. Review of Agricultural Economics, v. 23, n. 1, p. 19-32, 2001. Disponível em: <http://www.periodicos.capes.gov.br/portugues/index>. Acesso em abr. 09.
COELHO, A.B. A cultura do algodão e a questão da integração de preços internos e externos. Dissertação. Universidade de São Paulo, São Paulo, 2002. Disponível em <http://www.econ.fea.usp.br/pos-graduacao>. Acesso em: julho. 2009.
COSTA, S.M.A.L; FERREIRA FILHO, J.B.S. (2000); Liberalização comercial no Brasil e integração nos mercados de commodities agrícolas: os mercados de algodão, milho e arroz. Revista de Economia e Sociologia Rural, 38(2): 41-70, abr/jun.
CUNHA, D. A. DA. (2008); Integração de preços no mercado internacional do café. Viçosa, Dissertação (Mestrado em Economia Aplicada), UFV.
FACKLER, P.L., GOODWIN, B.K. (2000); Spatial price analysis: forthcoming, Handbook of Agricultural Economics. North-Holland. p. 1-59.
FAMINEW, M. D.; BENSON, B L. Integration of spatial markets. American of Agricultural Economics, v. 72 (1), p. 49-62, 1990. Disponível em: <http://www.periodicos.capes.gov .br/portugues/index>. Acesso em mar. 09
GONZÁLEZ-RIVERA, G., HELFAND, S.M. (2001); Economic development and determinants of spatial integration in agricultural markets. Riverside: University of California (Working Paper, 28).
GUJARATI, D. (2006) Econometria básica. São Paulo: Editora Campus.
KANNEBLEY Jr., S. (2000); “Exchenge Rate Pass-through: Uma Análise Setorial para as Exportações Brasileiras 1984-1997”. Economia Aplicada. São Paulo, v.4 (3): 435-463, 2000.
LOPES, T. A. M. (2008); Transmissão de preços do trigo entre países do Mercosul e Estados Unidos no período de 1995-2005. Santa Maria, Dissertação de Mestrado (mestrado em integração latino-americana), UFSM.
NOGUEIRA, F. T. P.; AGUIAR, D. R. D. ; LIMA, J. E. (2005); “Integração espacial no mercado brasileiro de café arábica”. Nova Economia. Belo Horizonte, n. 15 (2), p. 91-112, mai-ago.
PEREIRA, L.R.R. (2005); Integração espacial no mercado brasileiro de boi gordo. Viçosa, 166 p. Tese (Doutorado) – Universidade Federal de Viçosa, UFV.
PESARAN, M.H., SHIN, Y. (1996); “Cointegration and speed of convergence to equilibrium”. Journal of Econometrics, v. 71, p. 117-143.
ROSADO, P. L. (2006); Integração espacial entre os mercados brasileiros de suínos. Viçosa, Tese (Doutorado em Economia Aplicada), UFV.
SILVA, R. R. da. (2002); O agronegócio brasileiro da carne caprina e ovina. Salvador: R. R. da Silva, 111 p.
VIANA, J.G.A. (2008); Governança da cadeia produtiva da ovinocultura no rio grande do sul: estudo de caso à luz dos custos de transação e produção. Santa Maria, Dissertação de Mestrado (mestrado em extensão rural), UFSM.